Përcaktimi i metodës së matricës. Zgjidhja e sistemeve të ekuacioneve lineare duke përdorur metodën e matricës. Shembuj të zgjidhjes së një sistemi ekuacionesh lineare duke përdorur metodën e matricës
Le të shqyrtojmë sistemi i ekuacioneve algjebrike lineare(SLAU) relativisht n i panjohur x 1 , x 2 , ..., x n :
Ky sistem në një formë "të shembur" mund të shkruhet si më poshtë:
S n i=1 a ij x j = b i , i=1,2, ..., n.
Në përputhje me rregullin e shumëzimit të matricës, sistemi i konsideruar i ekuacioneve lineare mund të shkruhet në forma matrice Ax=b, Ku
Matricë A, kolonat e të cilave janë koeficientët për të panjohurat përkatëse, dhe rreshtat janë koeficientët për të panjohurat në ekuacionin përkatës quhet matricës së sistemit. Matrica e kolonës b, elementet e të cilit janë anët e djathta të ekuacioneve të sistemit, quhet matrica e krahut të djathtë ose thjesht anën e djathtë të sistemit. Matrica e kolonës x , elementet e të cilit janë të panjohurat e panjohura, quhet zgjidhje sistemi.
Një sistem ekuacionesh algjebrike lineare të shkruara në formë Ax=b, eshte ekuacioni i matricës.
Nëse matrica e sistemit jo i degjeneruar, atëherë ka një matricë të anasjelltë dhe pastaj zgjidhja e sistemit është Ax=b jepet me formulën:
x=A -1 b.
Shembull Zgjidheni sistemin  metoda e matricës.
metoda e matricës.
Zgjidhje le të gjejmë matricën e anasjelltë për matricën e koeficientit të sistemit

Le të llogarisim përcaktorin duke u zgjeruar përgjatë vijës së parë:

Sepse Δ ≠ 0 , Kjo A -1 ekziston.

Matrica e anasjelltë u gjet saktë.
Le të gjejmë një zgjidhje për sistemin 
Prandaj, x 1 = 1, x 2 = 2, x 3 = 3 .
Ekzaminimi: 
7. Teorema Kronecker-Capelli mbi përputhshmërinë e një sistemi ekuacionesh algjebrike lineare.
Sistemi i ekuacioneve lineare ka formën:
a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2, (5.1)
a m1 x 1 + a m1 x 2 +... + a mn x n = b m.
Këtu jepen a i j dhe b i (i = ; j = ) dhe x j janë numra realë të panjohur. Duke përdorur konceptin e produktit të matricave, ne mund ta rishkruajmë sistemin (5.1) në formën:
ku A = (a i j) është një matricë e përbërë nga koeficientë për të panjohurat e sistemit (5.1), e cila quhet matricës së sistemit, X = (x 1 , x 2 ,..., x n) T , B = (b 1 , b 2 ,..., b m) T janë vektorë kolonash të përbëra përkatësisht nga të panjohura x j dhe terma të lirë b i .
Mbledhja e porositur n quhen numra realë (c 1, c 2,..., c n). zgjidhje sistemi(5.1), nëse si rezultat i zëvendësimit të këtyre numrave në vend të variablave përkatëse x 1, x 2,..., x n, çdo ekuacion i sistemit kthehet në një identitet aritmetik; me fjalë të tjera, nëse ekziston një vektor C= (c 1 , c 2 ,..., c n) T i tillë që AC B.
Sistemi (5.1) quhet të përbashkët, ose e zgjidhshme, nëse ka të paktën një zgjidhje. Sistemi quhet të papajtueshme, ose e pazgjidhshme, nëse nuk ka zgjidhje.
 ,
,
e formuar duke caktuar një kolonë me terma të lirë në anën e djathtë të matricës A quhet matrica e zgjeruar e sistemit.
Çështja e përputhshmërisë së sistemit (5.1) zgjidhet me teoremën e mëposhtme.
Teorema Kronecker-Capelli . Një sistem ekuacionesh lineare është i qëndrueshëm nëse dhe vetëm nëse radhët e matricave A dheA përputhen, d.m.th. r(A) = r(A) = r.
Për grupin M të zgjidhjeve të sistemit (5.1) ekzistojnë tre mundësi:
1) M = (në këtë rast sistemi është jokonsistent);
2) M përbëhet nga një element, d.m.th. sistemi ka një zgjidhje unike (në këtë rast sistemi quhet të caktuara);
3) M përbëhet nga më shumë se një element (atëherë quhet sistemi i pasigurt). Në rastin e tretë, sistemi (5.1) ka një numër të pafund zgjidhjesh.
Sistemi ka një zgjidhje unike vetëm nëse r(A) = n. Në këtë rast, numri i ekuacioneve nuk është më i vogël se numri i të panjohurave (mn); nëse m>n, atëherë ekuacionet m-n janë pasoja të të tjerave. Nëse 0 Për të zgjidhur një sistem arbitrar të ekuacioneve lineare, duhet të jeni në gjendje të zgjidhni sisteme në të cilat numri i ekuacioneve është i barabartë me numrin e të panjohurave - të ashtuquajturat Sistemet e tipit kramer: a 11 x 1 + a 12 x 2 +... + a 1n x n = b 1, a 21 x 1 + a 22 x 2 +... + a 2n x n = b 2, (5.3) ...
... ... ...
... ... a n1 x 1 + a n1 x 2 +... + a nn x n = b n . Sistemet (5.3) zgjidhen në njërën nga mënyrat e mëposhtme: 1) metoda e Gausit, ose metoda e eliminimit të të panjohurave; 2) sipas formulave të Cramer; 3) metoda e matricës. Shembulli 2.12. Eksploroni sistemin e ekuacioneve dhe zgjidhni atë nëse është konsistent: 5x 1 - x 2 + 2x 3 + x 4 = 7, 2x 1 + x 2 + 4x 3 - 2x 4 = 1, x 1 - 3x 2 - 6x 3 + 5x 4 = 0. Zgjidhje. Ne shkruajmë matricën e zgjeruar të sistemit:
Le të llogarisim rangun e matricës kryesore të sistemit. Është e qartë se, për shembull, minorja e rendit të dytë në këndin e sipërm të majtë = 7 0; të miturit e rendit të tretë që e përmbajnë atë janë të barabartë me zero: Rrjedhimisht, rangu i matricës kryesore të sistemit është 2, d.m.th. r(A) = 2. Për të llogaritur rangun e matricës së zgjeruar A, merrni parasysh minorin kufitar kjo do të thotë se rangu i matricës së zgjeruar r(A) = 3. Meqenëse r(A) r(A), sistemi është jokonsistent. Në pjesën e parë kemi parë disa materiale teorike, metodën e zëvendësimit, si dhe metodën e mbledhjes term pas termi të ekuacioneve të sistemit. Unë rekomandoj të gjithë ata që kanë hyrë në faqe përmes kësaj faqeje të lexojnë pjesën e parë. Ndoshta disa vizitorëve do ta kenë materialin shumë të thjeshtë, por në procesin e zgjidhjes së sistemeve të ekuacioneve lineare, bëra një sërë komentesh dhe përfundimesh shumë të rëndësishme në lidhje me zgjidhjen e problemeve matematikore në përgjithësi. Tani do të analizojmë rregullin e Cramer-it, si dhe do të zgjidhim një sistem ekuacionesh lineare duke përdorur një matricë të kundërt (metoda e matricës). Të gjitha materialet janë paraqitur thjesht, në detaje dhe qartë; pothuajse të gjithë lexuesit do të jenë në gjendje të mësojnë se si të zgjidhin sistemet duke përdorur metodat e mësipërme. Së pari, do t'i hedhim një vështrim më të afërt rregullit të Cramer-it për një sistem me dy ekuacione lineare në dy të panjohura. Per cfare? – Në fund të fundit, sistemi më i thjeshtë mund të zgjidhet duke përdorur metodën e shkollës, metodën e mbledhjes term pas termi! Fakti është se, megjithëse ndonjëherë, ndodh një detyrë e tillë - të zgjidhet një sistem me dy ekuacione lineare me dy të panjohura duke përdorur formulat e Cramer. Së dyti, një shembull më i thjeshtë do t'ju ndihmojë të kuptoni se si të përdorni rregullin e Cramer për një rast më kompleks - një sistem prej tre ekuacionesh me tre të panjohura. Përveç kësaj, ekzistojnë sisteme ekuacionesh lineare me dy ndryshore, të cilat këshillohen të zgjidhen duke përdorur rregullin e Cramer! Konsideroni sistemin e ekuacioneve Në hapin e parë, ne llogarisim përcaktorin, quhet përcaktuesi kryesor i sistemit. Metoda e Gausit. Nëse , atëherë sistemi ka një zgjidhje unike dhe për të gjetur rrënjët duhet të llogarisim edhe dy përcaktues të tjerë: Në praktikë, kualifikuesit e mësipërm mund të shënohen edhe me një shkronjë latine. Ne gjejmë rrënjët e ekuacionit duke përdorur formulat: Shembulli 7 Zgjidh një sistem ekuacionesh lineare Zgjidhje: Shohim se koeficientët e ekuacionit janë mjaft të mëdhenj; në anën e djathtë ka thyesa dhjetore me presje. Presja është një mysafir mjaft i rrallë në detyrat praktike në matematikë; Unë e mora këtë sistem nga një problem ekonometrik. Si të zgjidhet një sistem i tillë? Mund të përpiqeni të shprehni një variabël në termat e një tjetri, por në këtë rast ndoshta do të përfundoni me fraksione të tmerrshme të zbukuruara me të cilat është jashtëzakonisht e papërshtatshme për të punuar, dhe dizajni i zgjidhjes do të duket thjesht i tmerrshëm. Ju mund të shumëzoni ekuacionin e dytë me 6 dhe të zbrisni term për term, por të njëjtat thyesa do të lindin edhe këtu. Çfarë duhet bërë? Në raste të tilla, formulat e Cramer vijnë në shpëtim. ; ; Përgjigju: , Të dyja rrënjët kanë bishta të pafund dhe gjenden afërsisht, gjë që është mjaft e pranueshme (dhe madje e zakonshme) për problemet ekonometrike. Komentet nuk nevojiten këtu, pasi detyra zgjidhet duke përdorur formula të gatshme, megjithatë, ekziston një paralajmërim. Kur përdorni këtë metodë, të detyrueshme Një fragment i dizajnit të detyrës është fragmenti i mëposhtëm: "Kjo do të thotë se sistemi ka një zgjidhje unike". Përndryshe, recensuesi mund t'ju ndëshkojë për mosrespektim të teoremës së Cramer-it. Nuk do të ishte e tepërt të kontrollohej, gjë që mund të kryhet me lehtësi në një kalkulator: ne zëvendësojmë vlerat e përafërta në anën e majtë të secilit ekuacion të sistemit. Si rezultat, me një gabim të vogël, duhet të merrni numra që janë në anët e duhura. Shembulli 8 Paraqisni përgjigjen në thyesa të zakonshme të pasakta. Bëni një kontroll. Ky është një shembull që ju duhet ta zgjidhni vetë (një shembull i modelit përfundimtar dhe përgjigja në fund të mësimit). Le të vazhdojmë të shqyrtojmë rregullin e Cramer për një sistem prej tre ekuacionesh me tre të panjohura: Gjejmë përcaktuesin kryesor të sistemit: Nëse , atëherë sistemi ka pafundësisht shumë zgjidhje ose është jokonsistent (nuk ka zgjidhje). Në këtë rast, rregulli i Cramer nuk do të ndihmojë; ju duhet të përdorni metodën e Gausit. Nëse , atëherë sistemi ka një zgjidhje unike dhe për të gjetur rrënjët duhet të llogarisim edhe tre përcaktues të tjerë: Dhe së fundi, përgjigjja llogaritet duke përdorur formulat: Siç mund ta shihni, rasti "tre nga tre" në thelb nuk ndryshon nga rasti "dy nga dy"; kolona e termave të lirë "ecën" në mënyrë sekuenciale nga e majta në të djathtë përgjatë kolonave të përcaktorit kryesor. Shembulli 9 Zgjidheni sistemin duke përdorur formulat e Cramer-it. Zgjidhje: Le të zgjidhim sistemin duke përdorur formulat e Cramer-it. Përgjigju: Në fakt, këtu përsëri nuk ka asgjë të veçantë për të komentuar, për faktin se zgjidhja ndjek formula të gatshme. Por ka disa komente. Ndodh që si rezultat i llogaritjeve të fitohen thyesa të pareduktueshme “të këqija” p.sh.: . 1) Mund të ketë një gabim në llogaritjet. Sapo të hasni një fraksion "të keq", menjëherë duhet të kontrolloni A është rishkruar si duhet kushti?. Nëse kushti rishkruhet pa gabime, atëherë duhet të rillogaritni përcaktuesit duke përdorur zgjerimin në një rresht (kolona) tjetër. 2) Nëse nuk identifikohen gabime si rezultat i kontrollit, atëherë ka shumë të ngjarë të ketë pasur një gabim shtypi në kushtet e detyrës. Në këtë rast, punoni me qetësi dhe me kujdes detyrën deri në fund, dhe më pas sigurohuni që të kontrolloni dhe ne e hartojmë atë në një fletë të pastër pas vendimit. Sigurisht, të kontrollosh një përgjigje të pjesshme është një detyrë e pakëndshme, por do të jetë një argument çarmatos për mësuesin, i cili me të vërtetë i pëlqen të japë një minus për çdo marrëzi si . Mënyra e trajtimit të thyesave përshkruhet në detaje në përgjigjen e Shembullit 8. Nëse keni një kompjuter në dorë, atëherë përdorni një program të automatizuar për të kontrolluar, i cili mund të shkarkohet falas që në fillim të mësimit. Nga rruga, është më e dobishme të përdorni programin menjëherë (edhe para se të filloni zgjidhjen); menjëherë do të shihni hapin e ndërmjetëm ku keni bërë një gabim! I njëjti kalkulator llogarit automatikisht zgjidhjen e sistemit duke përdorur metodën e matricës. Vërejtje e dytë. Herë pas here ka sisteme në ekuacionet e të cilave mungojnë disa variabla, për shembull: Shembulli 10 Zgjidheni sistemin duke përdorur formulat e Cramer-it. Ky është një shembull për një zgjidhje të pavarur (një mostër e modelit përfundimtar dhe përgjigja në fund të mësimit). Për rastin e një sistemi prej 4 ekuacionesh me 4 të panjohura, formulat e Cramer-it shkruhen sipas parimeve të ngjashme. Mund të shihni një shembull të drejtpërdrejtë në mësimin Vetitë e përcaktorëve. Zvogëlimi i rendit të përcaktorit - pesë përcaktorë të rendit të katërt janë mjaft të zgjidhshëm. Edhe pse detyra tashmë të kujton shumë këpucën e një profesori në gjoksin e një studenti me fat. Metoda e matricës së kundërt është në thelb një rast i veçantë ekuacioni i matricës(Shih shembullin nr. 3 të mësimit të specifikuar). Për të studiuar këtë seksion, duhet të jeni në gjendje të zgjeroni përcaktuesit, të gjeni inversin e një matrice dhe të kryeni shumëzimin e matricës. Lidhjet përkatëse do të sigurohen ndërsa shpjegimet përparojnë. Shembulli 11 Zgjidheni sistemin duke përdorur metodën e matricës Zgjidhje: Le ta shkruajmë sistemin në formë matrice: Ju lutemi shikoni sistemin e ekuacioneve dhe matricave. Unë mendoj se të gjithë e kuptojnë parimin me të cilin ne i shkruajmë elementet në matrica. Komenti i vetëm: nëse disa variabla do të mungonin në ekuacionet, atëherë zerat do të duhej të vendoseshin në vendet përkatëse në matricë. Ne gjejmë matricën e kundërt duke përdorur formulën: Së pari, le të shohim përcaktuesin: Këtu përcaktori zgjerohet në rreshtin e parë. Kujdes! Nëse , atëherë matrica e anasjelltë nuk ekziston dhe është e pamundur të zgjidhet sistemi duke përdorur metodën e matricës. Në këtë rast, sistemi zgjidhet me metodën e eliminimit të të panjohurave (metoda Gauss). Tani duhet të llogarisim 9 minore dhe t'i shkruajmë në matricën e të miturve Referenca:Është e dobishme të dihet kuptimi i nënshkrimeve të dyfishta në algjebër lineare. Shifra e parë është numri i rreshtit në të cilin ndodhet elementi. Shifra e dytë është numri i kolonës në të cilën ndodhet elementi: Le të na jepet një sistem ekuacionesh lineare me Do të supozojmë se matrica kryesore Komentoni.
Vini re se metoda e matricës për zgjidhjen e sistemeve të ekuacioneve lineare, në ndryshim nga metoda e Gausit, ka zbatim të kufizuar: kjo metodë mund të zgjidhë vetëm sisteme ekuacionesh lineare në të cilat, së pari, numri i të panjohurave është i barabartë me numrin e ekuacioneve, dhe së dyti, matrica kryesore është jo njëjës. Shembull.
Zgjidh një sistem ekuacionesh lineare duke përdorur metodën e matricës. Jepet një sistem me tre ekuacione lineare me tre të panjohura Matrica kryesore e sistemit të ekuacioneve është jo njëjës, pasi përcaktori i saj është jo zero: Matrica e anasjelltë Duke përdorur formulën e metodës së matricës për zgjidhjen e sistemeve të ekuacioneve lineare, marrim Kjo metodë, si metoda e matricës, është e zbatueshme vetëm për sistemet e ekuacioneve lineare në të cilat numri i të panjohurave përkon me numrin e ekuacioneve. Metoda e Cramer bazohet në teoremën me të njëjtin emër: Teorema 5.2.
Sistemi matrica kryesore e së cilës është jo njëjës, ka një zgjidhje unike që mund të merret duke përdorur formulat Ku Shembull.
Le të gjejmë zgjidhjen e sistemit të ekuacioneve lineare të shqyrtuara në shembullin e mëparshëm duke përdorur metodën e Cramer-it. Matrica kryesore e sistemit të ekuacioneve është jo e degjeneruar, pasi Duke përdorur formulat e paraqitura në Teoremën 5.2, ne llogarisim vlerat e të panjohurave: Zgjidhja bazë Të studiosh një sistem ekuacionesh lineare do të thotë të përcaktosh nëse ky sistem është i pajtueshëm apo i papajtueshëm, dhe nëse është i pajtueshëm, të zbulosh nëse ky sistem është i caktuar apo i pacaktuar. Kushti i përputhshmërisë për një sistem ekuacionesh lineare jepet nga teorema e mëposhtme Teorema 6.1 (Kronecker–Capelli).
Një sistem ekuacionesh lineare është i qëndrueshëm nëse dhe vetëm nëse rangu i matricës kryesore të sistemit është i barabartë me gradën e matricës së tij të zgjeruar: Për një sistem të njëkohshëm ekuacionesh lineare, çështja e definicitetit ose pasigurisë së tij zgjidhet duke përdorur teoremat e mëposhtme. Teorema 6.2.
Nëse rangu i matricës kryesore të një sistemi të përbashkët është i barabartë me numrin e të panjohurave, atëherë sistemi është i përcaktuar Teorema 6.3.
Nëse rangu i matricës kryesore të një sistemi të përbashkët është më i vogël se numri i të panjohurave, atëherë sistemi është i pasigurt. Kështu, nga teoremat e formuluara rrjedh një metodë për studimin e sistemeve të ekuacioneve algjebrike lineare. Le n- numri i të panjohurave, Përkufizimi 6.1.
Zgjidhja bazë e një sistemi të pacaktuar ekuacionesh lineare është një zgjidhje në të cilën të gjitha të panjohurat e lira janë të barabarta me zero. Shembull.
Eksploroni një sistem ekuacionesh lineare. Nëse sistemi është i pasigurt, gjeni zgjidhjen e tij bazë. Le të llogarisim radhët e kryesorit Shtoni rreshtin e dytë të matricës në rreshtin e parë të saj, shumëzuar me Në rreshtin e tretë të kësaj matrice shtojmë rreshtin e dytë të shumëzuar me duke hequr rreshtat e tretë dhe të katërt nga të cilët marrim një matricë hapash Kështu, E panjohur Le të jetë një matricë katrore e rendit të n-të Matrica A -1 quhet matricë e anasjelltë në lidhje me matricën A, nëse A*A -1 = E, ku E është matrica e identitetit të rendit të n-të. Matrica e identitetit- një matricë e tillë katrore në të cilën të gjithë elementët përgjatë diagonales kryesore, duke kaluar nga këndi i sipërm i majtë në këndin e poshtëm të djathtë, janë njësh, dhe pjesa tjetër janë zero, për shembull: matricë e anasjelltë mund të ekzistojë vetëm për matricat katrore ato. për ato matrica në të cilat numri i rreshtave dhe kolonave përputhet. Në mënyrë që një matricë të ketë një matricë të anasjelltë, është e nevojshme dhe e mjaftueshme që ajo të jetë jo njëjës. Matrica A = (A1, A2,...A n) quhet jo i degjeneruar, nëse vektorët e kolonës janë linearisht të pavarur. Numri i vektorëve të kolonës linearisht të pavarur të një matrice quhet rangu i matricës. Prandaj, mund të themi se për të ekzistuar një matricë e kundërt, është e nevojshme dhe e mjaftueshme që rangu i matricës të jetë i barabartë me dimensionin e saj, d.m.th. r = n. Për matricën A, gjeni matricën e anasjelltë A -1 Zgjidhje: Shkruajmë matricën A dhe caktojmë matricën e identitetit E në të djathtë. Duke përdorur transformimet e Jordanit, reduktojmë matricën A në matricën e identitetit E. Llogaritjet janë dhënë në tabelën 31.1. Le të kontrollojmë korrektësinë e llogaritjeve duke shumëzuar matricën origjinale A dhe matricën e kundërt A -1. Si rezultat i shumëzimit të matricës, u mor matrica e identitetit. Prandaj, llogaritjet janë bërë në mënyrë korrekte. Përgjigje: Ekuacionet e matricës mund të duken si: AX = B, HA = B, AXB = C, ku A, B, C janë matricat e specifikuara, X është matrica e dëshiruar. Ekuacionet e matricës zgjidhen duke shumëzuar ekuacionin me matricat e anasjellta.
Për shembull, për të gjetur matricën nga ekuacioni, duhet ta shumëzoni këtë ekuacion me në të majtë. Prandaj, për të gjetur një zgjidhje për ekuacionin, duhet të gjeni matricën e kundërt dhe ta shumëzoni atë me matricën në anën e djathtë të ekuacionit. Ekuacionet e tjera zgjidhen në mënyrë të ngjashme. Zgjidheni ekuacionin AX = B nëse Zgjidhje: Meqenëse matrica e kundërt është e barabartë me (shih shembullin 1) Së bashku me të tjerat, ato përdoren edhe metodat e matricës. Këto metoda bazohen në algjebër lineare dhe me matricë vektoriale. Metoda të tilla përdoren për qëllime të analizimit të dukurive ekonomike komplekse dhe shumëdimensionale. Më shpesh, këto metoda përdoren kur është e nevojshme të bëhet një vlerësim krahasues i funksionimit të organizatave dhe ndarjeve strukturore të tyre. Në procesin e aplikimit të metodave të analizës së matricës, mund të dallohen disa faza. Në fazën e parëështë duke u formuar një sistem treguesish ekonomikë dhe mbi bazën e tij përpilohet një matricë e të dhënave fillestare, e cila është një tabelë në të cilën numrat e sistemit tregohen në rreshtat e tij individualë. (i = 1,2,....,n), dhe në kolonat vertikale - numrat e treguesve (j = 1,2,....,m). Në fazën e dytë Për secilën kolonë vertikale, identifikohet vlera më e madhe e treguesit në dispozicion, e cila merret si një. Pas kësaj, të gjitha shumat e pasqyruara në këtë kolonë ndahen me vlerën më të madhe dhe formohet një matricë e koeficientëve të standardizuar. Në fazën e tretë të gjithë komponentët e matricës janë në katror. Nëse ato kanë rëndësi të ndryshme, atëherë çdo treguesi të matricës i caktohet një koeficient i caktuar peshe k. Vlera e kësaj të fundit përcaktohet nga ekspertiza. Në të fundit, faza e katërt gjetur vlerat e vlerësimit R j grupohen sipas rritjes ose uljes së tyre. Metodat e matricës të përshkruara duhet të përdoren, për shembull, në një analizë krahasuese të projekteve të ndryshme investuese, si dhe në vlerësimin e treguesve të tjerë ekonomikë të aktiviteteve të organizatave. Metoda e matricës së kundërt nuk është e vështirë nëse i njihni parimet e përgjithshme të punës me ekuacionet e matricës dhe, natyrisht, dini të kryeni veprime elementare algjebrike. Zgjidhja e një sistemi ekuacionesh duke përdorur metodën e matricës së kundërt. Shembull. Mënyra më e përshtatshme për të kuptuar metodën e matricës së kundërt është me një shembull të qartë. Le të marrim një sistem ekuacionesh: Hapi i parë për të zgjidhur këtë sistem ekuacionesh është gjetja e përcaktorit. Prandaj, le të transformojmë sistemin tonë të ekuacioneve në matricën e mëposhtme: Dhe gjejmë përcaktuesin e nevojshëm: Formula e përdorur për zgjidhjen e ekuacioneve të matricës është si më poshtë: Kështu, për të llogaritur X, duhet të përcaktojmë vlerën e matricës A-1 dhe ta shumëzojmë atë me b. Një formulë tjetër do të na ndihmojë me këtë: Në këtë rast do të jetë matrica e transpozuar- domethënë i njëjti origjinal, por i shkruar jo në rreshta, por në kolona. Këtë nuk duhet ta harrojmë metoda e matricës së kundërt, si metoda e Cramer-it, është e përshtatshme vetëm për sistemet në të cilat përcaktori është më i madh ose më i vogël se zero. Nëse përcaktori është i barabartë me zero, duhet të përdorni metodën Gaussian. Hapi tjetër është përpilimi i një matrice të të miturve, e cila është skema e mëposhtme: Si rezultat, ne morëm tre matrica - të vogla, shtesa algjebrike dhe një matricë të transpozuar të shtesave algjebrike. Tani mund të vazhdoni me përpilimin aktual të matricës së kundërt. Ne tashmë e dimë formulën. Për shembullin tonë do të duket kështu. .
.


Dhe
, ![]()
![]()
![]()


 ,
,  ,
, 
![]()


, që do të thotë se sistemi ka një zgjidhje unike.
![]()

![]()

![]()
![]() .
.
Unë rekomandoj algoritmin e mëposhtëm të "trajtimit". Nëse nuk keni një kompjuter në dorë, bëni këtë:
Këtu në ekuacionin e parë nuk ka variabël, në të dytin nuk ka ndryshore. Në raste të tilla, është shumë e rëndësishme të shkruani saktë dhe me kujdes përcaktuesin kryesor:  – zero vendosen në vend të variablave që mungojnë.
– zero vendosen në vend të variablave që mungojnë.
Nga rruga, është racionale të hapen përcaktuesit me zero sipas rreshtit (kolonës) në të cilën ndodhet zeroja, pasi ka dukshëm më pak llogaritje.
Zgjidhja e sistemit duke përdorur një matricë të kundërt

, Ku 
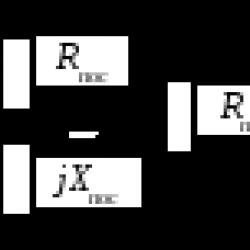
, ku është matrica e transpozuar e plotësimeve algjebrike të elementeve përkatëse të matricës.


Kjo do të thotë, një nënshkrim i dyfishtë tregon që elementi është në rreshtin e parë, kolonën e tretë dhe, për shembull, elementi është në 3 rreshta, 2 kolona i panjohur:
i panjohur:



 jo i degjeneruar. Pastaj, nga teorema 3.1, ekziston një matricë e anasjelltë
jo i degjeneruar. Pastaj, nga teorema 3.1, ekziston një matricë e anasjelltë  Shumëzimi i ekuacionit të matricës
Shumëzimi i ekuacionit të matricës  te matrica
te matrica  në të majtë, duke përdorur përkufizimin 3.2, si dhe deklaratën 8) të teoremës 1.1, marrim formulën në të cilën bazohet metoda e matricës për zgjidhjen e sistemeve të ekuacioneve lineare:
në të majtë, duke përdorur përkufizimin 3.2, si dhe deklaratën 8) të teoremës 1.1, marrim formulën në të cilën bazohet metoda e matricës për zgjidhjen e sistemeve të ekuacioneve lineare:

 Ku
Ku



 Le të hartojmë duke përdorur një nga metodat e përshkruara në paragrafin 3.
Le të hartojmë duke përdorur një nga metodat e përshkruara në paragrafin 3.

5.3. Metoda Cramer
 ekuacionet lineare me
ekuacionet lineare me  i panjohur
i panjohur

 përcaktor i një matrice që rrjedh nga matrica bazë
përcaktor i një matrice që rrjedh nga matrica bazë  sistemi i ekuacioneve duke e zëvendësuar atë
sistemi i ekuacioneve duke e zëvendësuar atë  kolona e th me një kolonë anëtarësh të lirë.
kolona e th me një kolonë anëtarësh të lirë. Le të llogarisim përcaktorët
Le të llogarisim përcaktorët 



6. Studimi i sistemeve të ekuacioneve lineare.


 Pastaj:
Pastaj:

 dhe matricat e zgjeruara
dhe matricat e zgjeruara  të këtij sistemi ekuacionesh, për të cilin e sjellim matricën e zgjeruar (dhe në të njëjtën kohë kryesore) të sistemit në një formë hap pas hapi:
të këtij sistemi ekuacionesh, për të cilin e sjellim matricën e zgjeruar (dhe në të njëjtën kohë kryesore) të sistemit në një formë hap pas hapi:
 rreshti i tretë - me rreshtin e parë të shumëzuar me
rreshti i tretë - me rreshtin e parë të shumëzuar me  dhe rreshti i katërt - me të parën, shumëzuar me
dhe rreshti i katërt - me të parën, shumëzuar me  marrim një matricë
marrim një matricë
 dhe në rreshtin e katërt - i pari, shumëzuar me
dhe në rreshtin e katërt - i pari, shumëzuar me  Si rezultat, marrim matricën
Si rezultat, marrim matricën


 Rrjedhimisht, ky sistem ekuacionesh lineare është konsistent dhe duke qenë se vlera e renditjes është më e vogël se numri i të panjohurave, sistemi është i pasigurt.Matrica e hapave e përftuar si rezultat i transformimeve elementare i korrespondon sistemit të ekuacioneve
Rrjedhimisht, ky sistem ekuacionesh lineare është konsistent dhe duke qenë se vlera e renditjes është më e vogël se numri i të panjohurave, sistemi është i pasigurt.Matrica e hapave e përftuar si rezultat i transformimeve elementare i korrespondon sistemit të ekuacioneve Dhe
Dhe  janë kryesoret, dhe të panjohurat
janë kryesoret, dhe të panjohurat  Dhe
Dhe  falas. Duke caktuar vlera zero për të panjohurat e lira, marrim një zgjidhje bazë për këtë sistem ekuacionesh lineare.
falas. Duke caktuar vlera zero për të panjohurat e lira, marrim një zgjidhje bazë për këtë sistem ekuacionesh lineare.

Teorema për kushtin e ekzistencës së një matrice të anasjelltë
Algoritmi për gjetjen e matricës së kundërt
Shembulli 1 



Zgjidhja e ekuacioneve të matricës


Metoda e matricës në analizën ekonomike