1. Le të marrim një trekëndësh të rregullt.
2. Presim një trekëndësh prej tij, kulmet e të cilit shtrihen në mesin e anëve të atij origjinali. Si rezultat, marrim tre trekëndësha në aeroplan, sipërfaqja e secilës prej të cilave është katër herë më e vogël se sipërfaqja e asaj origjinale.
3. Ne kryejmë manipulimet e mëparshme me trekëndëshat që rezultojnë.

Procesi duket si ky:

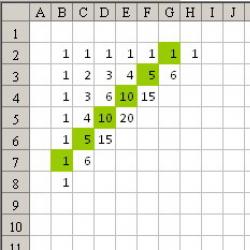
1. Është interesante, nëse në trekëndëshin e Paskalit të gjithë numrat tek janë të ngjyrosur me një ngjyrë dhe numrat çift një tjetër, atëherë formohet një trekëndësh Sierpinski.

Le të përfitojmë nga ky fakt. Vetëm në Excel është më i përshtatshëm të përdoret jo forma klasike (rresht pas rreshti) e trekëndëshit të Pascal, por kjo:

Këtu koeficientët binomialë shkruhen diagonalisht, në rreshtin e parë të mbushur dhe në kolonën e parë të mbushur të unitetit, dhe në pjesën tjetër shuma e elementeve të sipërme dhe të majta.

Le të kalojmë në ndërtim. Për ne mjafton të shkruajmë jo koeficientët, por vetëm barazinë e tyre.

Së pari, le të bëjmë madhësinë e qelizave në Excel, për shembull 7 me 7 piksele.

Le të qëndrojmë në qelizën B2, pastaj zgjidhni zonën B2:DY129 - për ta bërë këtë, shtypni Ctrl + G dhe shkruani B2:DY129 në fushën e lidhjes.

Tani në shiritin e formulave ne shkruajmë =IF(OR(ROW()=2,COLUMN()=2),1,REM(A2+B1,2))
dhe shtypni Ctrl + Enter për të mbushur të gjithë zonën e zgjedhur me një formulë të ngjashme.

Shkojme Menu - Formatimi i kushtëzuar dhe për vlerën 1 tregojmë ngjyrën e qelizës.

Si rezultat marrim:

Duhet të theksohet se trekëndëshi i Sierpinskit përftohet nga një lloj ecjeje e rastësishme në aeroplan. Gjegjësisht:

1. Le të rregullojmë 3 kulme të trekëndëshit në rrafsh dhe të marrim një pikë tjetër.
2. Ne marrim pikën e parë si mes të segmentit ndërmjet rastësisht kulmin dhe pikën e zgjedhur nga hapi 1.
3. Ne marrim pikën e dytë si mesin e segmentit ndërmjet rastësisht kulmin e zgjedhur dhe pikën e parë.
4. Ne e përsërisim procesin shumë herë.

Ju mund të përdorni këtë makro:

Nën-Makro publike()

Dim arRange (1 deri në 3) si varg
Dim tekRow si numër i plotë
Dim tekColumn si numër i plotë
Dim i Si numër i plotë
Dim it si numër i plotë

tekRow = Int(1000 * Rnd) + 1
tekColumn = Int(200 * Rnd) + 1

Cakto arRange (1) = Qeliza (1, 1)
Cakto arRange (2) = Qeliza (50, 250)
Cakto arRange (3) = Qeliza (200, 20)

Qelizat.E qartë

Për i = 1 deri në 20000
iT = (Int(1000 * Rnd) Mod 3) + 1
tekRow = Int((tekRow + arRange(iT).Rresht) / 2)
tekColumn = Int((tekColumn + arRange(iT).Column) / 2)
Cells(tekRow, tekColumn).Interior.Index Color = 5
Tjetra

Fundi Nën

Trekëndëshi i Sierpinskit- një fraktal, një nga analogët dydimensionale të grupit Cantor, i propozuar nga matematikani polak Waclaw Sierpinski në 1915. E njohur edhe si "pecetë" e Sierpinskit.

Trekëndëshi i Sierpinskit

Ndërtimi

Metoda përsëritëse

Ndërtimi i trekëndëshit të Sierpinskit

Pikat e mesit të brinjëve të një trekëndëshi barabrinjës janë të lidhura me segmente. Ju merrni 4 trekëndësha të rinj. Pjesa e brendshme e trekëndëshit të mesëm hiqet nga trekëndëshi origjinal. Rezulton shumë T 1 (\displaystyle T_(1)), i përbërë nga 3 trekëndëshat e mbetur të "rangut të parë". Duke bërë saktësisht të njëjtën gjë me secilin nga trekëndëshat e rangut të parë, marrim grupin T 2 (\displaystyle T_(2)), i përbërë nga 9 trekëndësha barabrinjës të rangut të dytë. Duke vazhduar këtë proces pafundësisht, marrim një sekuencë të pafundme T 0 ⊃ T 1 ⊃ ⋯ ⊃ T n ⊃ … (\shfaqja e stilit T_(0)\supset T_(1)\supset \dots \supset T_(n)\supset \dots ), kryqëzimi i anëtarëve të të cilit është një trekëndësh Sierpinski.

Metoda e Kaosit

1. Përcaktohen koordinatat e tërheqësve - kulmet e trekëndëshit origjinal T 0 (\displaystyle T_(0)). 2. Hapësira e probabilitetit (0 ; 1) (\displaystyle (0;1)) ndahet në 3 pjesë të barabarta, secila prej të cilave korrespondon me një tërheqës. 3. Përcaktohet një pikënisje e caktuar P 0 (\displaystyle P_(0)), i shtrirë brenda trekëndëshit T 0 (\displaystyle T_(0)). 4. Fillimi i ciklit të ndërtimit të pikave që i përkasin grupit të trekëndëshit të Sierpinskit. 1. Gjenerohet një numër i rastësishëm n ∈ (0 ; 1) (\displaystyle n\in (0;1)). 2. Tërheqësi aktiv bëhet kulmi në nënhapësirën probabilistike të së cilës ka rënë numri i gjeneruar. 3. Po ndërtohet një pikë P i (\displaystyle P_(i)) me koordinata të reja: x i = x i − 1 + x A 2 ; y i = y i − 1 + y A 2 (\displaystyle x_(i)=(\frac (x_(i-1)+x_(A))(2));y_(i)=(\frac (y_(i -1)+y_(A))(2))), Ku: x i − 1 , y i − 1 (\shfaqja e stilit x_(i-1),y_(i-1))- koordinatat e pikës së mëparshme P i − 1 (\displaystyle P_(i-1)); x A , y A (\style ekrani x_(A),y_(A))- koordinatat e pikës aktive tërheqëse. 5. Kthehuni në fillim të ciklit.

Vetitë

Ndërtimi me metodë iterative

Ndërtimi duke përdorur metodën e kaosit

Shënime

Lidhjet

L-sistemi

Sistemi L ose sistemi Lindenmayer është një sistem paralel rishkrimi dhe një lloj gramatike formale. Sistemi L përbëhet nga një alfabet simbolesh që mund të përdoren për të krijuar vargje, një grup rregullash gjeneruese që specifikojnë rregullat për zëvendësimin e secilit simbol, një varg fillestar ("aksiomë") nga i cili fillon ndërtimi dhe një mekanizëm për duke përkthyer vargun e krijuar në struktura gjeometrike. L-sistemet u propozuan dhe u zhvilluan në vitin 1968 nga Aristide Lindenmayer, një biolog dhe botanist hungarez në Universitetin e Utrecht. Lindenmayer përdori sistemet L për të përshkruar sjelljen e qelizave bimore dhe për të modeluar procesin e zhvillimit të bimëve. L-sistemet janë përdorur gjithashtu për të modeluar morfologjinë e organizmave të ndryshëm dhe mund të përdoren për të gjeneruar fraktale të ngjashme, siç janë sistemet e funksioneve të përsëritura.

Raket (gjuhë programimi)

Racket (më parë PLTScheme) është një gjuhë programimi me qëllime të përgjithshme me shumë paradigma që i përket familjes Lisp/Scheme. Ofron një mjedis për programim të orientuar drejt gjuhës - një nga qëllimet e raketës është krijimi, zhvillimi dhe zbatimi i gjuhëve programuese. Gjuha përdoret në kontekste të ndryshme: si gjuhë shkrimi, si gjuhë për qëllime të përgjithshme, në mësimdhënien e shkencave kompjuterike, në kërkimin shkencor.

Platforma i ofron përdoruesit një implementim të gjuhës Racket, duke përfshirë një sistem të zhvilluar të kohës së ekzekutimit, biblioteka të ndryshme, një përpilues JIT, etj., si dhe mjedisin e zhvillimit DrRacket (i njohur më parë si DrScheme) të shkruar në Racket. Ky kuadër softuerësh përdoret në kursin ProgramByDesign të MIT. Gjuha kryesore Racket përmban një sistem të fuqishëm makro që ju lejon të krijoni gjuhë programimi të integruara dhe specifike për domenin, konstruksione gjuhësore (për shembull, klasa dhe module) dhe dialekte Racket me semantikë të ndryshme.

Sistemi është softuer falas dhe me burim të hapur i shpërndarë sipas kushteve të LGPL. Shtesat dhe paketat e shkruara nga komuniteti janë të disponueshme në PLaneT, shpërndarjen në internet të sistemit.

Algoritmi i ngjeshjes fraktale

Kompresimi i imazhit fraktal është një algoritëm i kompresimit të imazhit me humbje i bazuar në aplikimin e sistemeve të funksioneve të përsëritura (zakonisht transformimet afinale) në imazhe. Ky algoritëm është i njohur për faktin se në disa raste mundëson marrjen e raporteve shumë të larta të kompresimit me cilësi vizuale të pranueshme për fotografi reale të objekteve natyrore. Për shkak të situatës së vështirë me patentim, algoritmi nuk u përdor gjerësisht.

Pllakë ndarëse

Rep-tile është një koncept i gjeometrisë së mozaikut, një figurë që mund të pritet në kopje më të vogla të vetë figurës. Në vitin 2012, një përgjithësim i pllakave ndarëse të quajtur grupi i pllakave vetë-tjegulluese u propozua nga matematikani anglez Lee Salous në Mathematics Magazine.

Rregulli përfundimtar i nënndarjes

Në matematikë, rregulli përfundimtar i nënndarjes është një mënyrë rekursive për të ndarë një shumëkëndësh dhe forma të tjera dydimensionale në copa gjithnjë e më të vogla. Rregullat e nënndarjes në këtë kuptim janë një përgjithësim i fraktaleve. Në vend që të përsërisni të njëjtin model pa pushim, ka ndryshime delikate në çdo hap, duke lejuar struktura më të pasura duke ruajtur ende stilin elegant fraktal. Rregullat e nënndarjes përdoren në arkitekturë, biologji dhe shkenca kompjuterike, si dhe në studimin e manifoldeve hiperbolike. Zëvendësimet e pllakave janë një lloj rregulli i nënndarjes i studiuar mirë.

Kurba Peano

Kurba Peano është një emër i përgjithshëm për kthesat parametrike, imazhi i të cilave përmban një katror (ose, në përgjithësi, rajone të hapura të hapësirës). Një emër tjetër është një kurbë që mbush hapësirën.

E emëruar pas Giuseppe Peano (1858-1932), zbuluesi i kësaj lloj kurbe, kurba Peano është emri i dhënë kurbës specifike që gjeti Peano.

Kurba e Sierpinskit

Kurbat e Sierpinskitështë një sekuencë e përcaktuar në mënyrë rekursive e kthesave fraktalike planare të mbyllura të vazhdueshme të zbuluara nga Waclaw Sierpinski. Lakorja në kufirin në plotëson plotësisht katrorin e njësisë, kështu që kurba e kufirit quhet gjithashtu Kurba e Sierpinskit, është një shembull i kurbave të mbushjes së hapësirës.

Meqenëse kurba e Sierpinskit mbush hapësirën, dimensioni i saj Hausdorff (në kufirin në n → ∞ (\displaystyle n\arrow djathtas \infty)) është e barabartë me 2 (\displaystyle 2).
Gjatësia e kurbës Euklidiane

e barabartë me l n = 2 3 (1 + 2) 2 n − 1 3 (2 − 2) 1 2 n (\displaystyle l_(n)=(2 \mbi 3)(1+(\sqrt (2)))2^( n)-(1 \mbi 3)(2-(\sqrt (2)))(1 \mbi 2^(n))),

dmth është në rritje në mënyrë eksponenciale Nga n (\displaystyle n), dhe kufiri në n → ∞ (\displaystyle n\arrow djathtas \infty) zona e rajonit të mbyllur nga kurba S n (\displaystyle S_(n)), eshte 5/12 (\displaystyle 5/12) katror (në metrikën Euklidiane).

Logaritmi

Logaritmi i një numri b (\displaystyle b) bazuar në a (\displaystyle a) (nga greqishtja e lashtë. λόγος "fjalë; qëndrim" + ἀριθμός "numri") përcaktohet si një tregues i fuqisë në të cilën baza duhet të ngrihet a (\displaystyle a) për të marrë numrin b (\displaystyle b). Përcaktimi: log a ⁡ b (\displaystyle \log _(a)b), shqiptohet: " logaritmi b (\displaystyle b) bazuar në a (\displaystyle a) ».

Nga përkufizimi del se konstatim x = log a ⁡ b (\displaystyle x=\log _(a)b)është e barabartë me zgjidhjen e ekuacionit a x = b (\displaystyle a^(x)=b). Për shembull, log 2 ⁡ 8 = 3 (\displaystyle \log _(2)8=3), sepse 2 3 = 8 (\displaystyle 2^(3)=8).

Llogaritja e logaritmit quhet nga logaritmi. Numrat a , b (\displaystyle a,b) më shpesh reale, por ekziston edhe një teori e logaritmeve komplekse.

Logaritmet kanë veti unike që kanë përcaktuar përdorimin e tyre të gjerë për të thjeshtuar ndjeshëm llogaritjet intensive të punës. Kur lëvizni "në botën e logaritmeve", shumëzimi zëvendësohet nga një mbledhje shumë më e thjeshtë, ndarja zëvendësohet me zbritjen dhe fuqizimi dhe nxjerrja e rrënjës shndërrohen, përkatësisht, në shumëzim dhe pjesëtim me eksponent. Laplace tha se shpikja e logaritmeve, "duke shkurtuar punën e astronomit, dyfishoi jetën e tij".

Përkufizimi i logaritmeve dhe një tabelë e vlerave të tyre (për funksionet trigonometrike) u botua për herë të parë në 1614 nga matematikani skocez John Napier. Tabelat logaritmike, të zgjeruara dhe të rafinuara nga matematikanë të tjerë, u përdorën gjerësisht për llogaritjet shkencore dhe inxhinierike për më shumë se tre shekuj, deri në shfaqjen e kalkulatorëve dhe kompjuterëve elektronikë.

Me kalimin e kohës, u bë e qartë se funksioni logaritmik y = log a ⁡ x (\displaystyle y=\log _(a)x)është i pazëvendësueshëm në shumë fusha të tjera të veprimtarisë njerëzore: zgjidhja e ekuacioneve diferenciale, klasifikimi i vlerave të sasive (për shembull, frekuenca dhe intensiteti i zërit), përafrimi i varësive të ndryshme, teoria e informacionit, teoria e probabilitetit, etj. Ky funksion është një nga ato elementare, është e anasjellta e funksionit eksponencial. Më të përdorurat janë logaritmet reale me baza 2 (\displaystyle 2)(binar), e (\displaystyle e) (logaritmi natyror) dhe 10 (\displaystyle 10)(dhjetore).

Nanoteknologji e bazuar në ADN

Nanoteknologjia e ADN-së është zhvillimi dhe prodhimi i strukturave artificiale nga acidet nukleike për përdorim teknologjik. Në këtë fushë shkencore, acidet nukleike përdoren jo si bartës të informacionit gjenetik në qelizat e gjalla, por si një material për nevojat e inxhinierisë jo-biologjike të nanomaterialeve.

Teknologjia përdor rregulla strikte për çiftimin e bazave të acideve nukleike, të cilat lejojnë vetëm pjesët e fijeve me sekuenca bazë plotësuese të lidhen së bashku për të formuar një strukturë të fortë dhe të ngurtë spirale të dyfishtë. Nga këto rregulla, bëhet e mundur të projektohen sekuenca të bazave që do të montohen në mënyrë selektive për të formuar struktura komplekse objektive me forma dhe veti të akorduara në shkallë nano. Shumica e materialeve janë bërë duke përdorur ADN-në, por strukturat që përfshijnë acide të tjera nukleike si ARN dhe acidet nukleike peptide (PNA) janë ndërtuar gjithashtu, duke lejuar që fusha e teknologjisë të quhet "nanoteknologji e bazës nukleotide".

Koncepti bazë i nanoteknologjisë së bazuar në ADN u propozua për herë të parë në fillim të viteve 1980 nga Nadrian Seaman dhe kjo fushë kërkimore filloi të tërheqë interes të gjerë në mesin e viteve 2000. Studiuesit që punojnë në këtë fushë të teknologjisë në zhvillim kanë krijuar struktura statike si rrjeta kristalore dy dhe tre-dimensionale, nanotuba, poliedra dhe forma të tjera në formë të lirë, si dhe struktura funksionale si makinat molekulare dhe kompjuterët e ADN-së.

Një shumëllojshmëri teknikash përdoren për të montuar këto struktura, duke përfshirë strukturimin e pllakave, ku pllakat mblidhen nga struktura më të vogla, strukturat e palosshme të krijuara duke përdorur teknikën e origami të ADN-së dhe strukturat e riorganizuara dinamikisht të krijuara duke përdorur teknikat e zhvendosjes së fijeve. Fusha e kërkimit ka filluar të përdoret si një mjet për zgjidhjen e problemeve të shkencës bazë në fushat e biologjisë strukturore dhe biofizikës, duke përfshirë problemet e aplikuara të kristalografisë dhe spektroskopisë për përcaktimin e strukturës së proteinave. Hulumtimi është gjithashtu duke u zhvilluar për aplikime të mundshme në elektronikën molekulare të shkallëzuar dhe nanomjekësinë.

Logaritmi natyror

Logaritmi natyrorështë logaritmi me bazën e, Ku e (\displaystyle e)- një konstante irracionale e barabartë me afërsisht 2.72. Është shënuar si ln ⁡ x (\displaystyle \ln x), log e ⁡ x (\displaystyle \log _(e)x) ose ndonjëherë vetëm log ⁡ x (\displaystyle \log x), nëse baza e (\displaystyle e) të nënkuptuara. Zakonisht numri x (\displaystyle x) nën shenjën e logaritmit është real, por ky koncept mund të shtrihet në numra komplekse.

Nga përkufizimi del se varësia logaritmike është funksioni i anasjelltë për eksponencialin y = e x (\displaystyle y=e^(x)), prandaj grafikët e tyre janë simetrik në lidhje me përgjysmuesin e kuadrantit të parë dhe të tretë (shih figurën në të djathtë). Ashtu si funksioni eksponencial, funksioni logaritmik i përket kategorisë së funksioneve transcendentale.

Logaritmet natyrore janë të dobishme për zgjidhjen e ekuacioneve algjebrike në të cilat e panjohura është e pranishme si eksponent dhe ato janë të domosdoshme në analizën matematikore. Për shembull, logaritmet përdoren për të gjetur konstanten e zbërthimit për një gjysmë jetë të njohur ose për të gjetur kohën e zbërthimit në zgjidhjen e problemeve të radioaktivitetit. Ato luajnë një rol të rëndësishëm në shumë fusha të matematikës dhe shkencave të aplikuara, dhe përdoren në financa për të zgjidhur shumë probleme, duke përfshirë gjetjen e interesit të përbërë.

Dimensioni Lebesgue

Dimensioni Lebesgue ose dimension topologjik- dimensioni i përcaktuar nga mbulesat, invarianti më i rëndësishëm i hapësirës topologjike. Dimensioni Lebesgue i hapësirës X (\displaystyle X) zakonisht shënohet dim ⁡ X (\displaystyle \dim X).

Rekursioni

Rekursioni është një përkufizim, përshkrim, imazh i një objekti ose procesi brenda këtij objekti ose procesi, domethënë një situatë kur një objekt është pjesë e vetvetes. Termi "rekursion" përdoret në fusha të ndryshme të specializuara të njohurive - nga gjuhësia në logjikë, por përdoret më gjerësisht në matematikë dhe shkenca kompjuterike.

Sierpinski, Waclaw

Wacław Franciszek Sierpiński, në një transkriptim tjetër - Sierpiński (polonisht: Wacław Franciszek Sierpiński; 14 mars 1882, Varshavë - 21 tetor 1969, po aty) - Matematikan dhe mësues polak, i njohur për veprat e tij në teorinë e aksiomës, zgjedhjen, hipoteza e vazhdimësisë, teoria e numrave, teoria e funksionit dhe topologjia. Autor i 724 artikujve dhe 50 librave.

Tetrahedron (Bottrop)

Tetraedri (gjermanisht: Tetraeder) është një strukturë çeliku në formën e një katërkëndëshi me gjatësi buzë 60 m, e mbështetur nga katër mbështetëse betoni 9 metra, e përdorur si një kuvertë vëzhgimi, në qytetin Bottrop (North Rhine-Westphalia). . Tetraedri ndodhet në majë të grumbullit të mbetjeve Beckstraße (gjermanisht: Beckstraße) të minierës Prosper-Haniel (de: Bergwerk Prosper-Haniel) në një lartësi prej 105 m mbi nivelin e detit. Nga kuverta e lartë e vëzhgimit mund të shihni pamjet e qyteteve të Bottrop, Essen, Oberhausen, Gladbeck. Me shikueshmëri të mirë, diapazoni i shikimit arrin 40 km dhe madje ju lejon të dalloni kullën televizive Rheinturm në Düsseldorf.

Bottrop Tetrahedron është pika tematike e projektit rajonal "Rruga e Kulturës Industriale" të rajonit të Ruhr.

trekëndëshi i Paskalit

Trekëndëshi i Paskalit është një tabelë e pafundme koeficientësh binomialë që kanë një formë trekëndore. Në këtë trekëndësh, ka në krye dhe në anët. Çdo numër është i barabartë me shumën e dy numrave mbi të. Vijat e trekëndëshit janë simetrike rreth boshtit vertikal. Me emrin Blaise Pascal. Numrat që përbëjnë trekëndëshin e Paskalit lindin natyrshëm në algjebër, kombinatorikë, teori probabiliteti, analizë matematikore dhe teori të numrave.

Fraktal

Fraktal (lat. fractus - i grimcuar, i thyer, i thyer) është një grup që ka vetinë e vetëngjashmërisë (një objekt që përkon saktësisht ose afërsisht me një pjesë të vetvetes, domethënë e tëra ka të njëjtën formë si një ose më shumë. pjesë). Në matematikë, fraktalet kuptohen si grupe pikash në hapësirën Euklidiane që kanë një dimension metrik të pjesshëm (në kuptimin e Minkowski ose Hausdorff), ose një dimension metrik të ndryshëm nga ai topologjik, kështu që ato duhet të dallohen nga figurat e tjera gjeometrike të kufizuara nga një numër i kufizuar lidhjesh. Figurat e vetë të ngjashme që përsëriten një numër të kufizuar herë quhen parafraktale.

Shembujt e parë të grupeve të ngjashme me veti të pazakonta u shfaqën në shekullin e 19-të si rezultat i studimit të funksioneve të vazhdueshme jo të diferencueshme (për shembull, funksioni Bolzano, funksioni Weierstrass, grupi Cantor). Termi "fraktal" u prezantua nga Benoit Mandelbrot në 1975 dhe u bë i njohur gjerësisht me botimin e librit të tij "Gjeometria Fraktal e Natyrës" në 1977. Fraktalet fituan një popullaritet të veçantë me zhvillimin e teknologjive kompjuterike, të cilat bënë të mundur vizualizimin efektiv të këtyre strukturave.

Fjala "fraktal" përdoret jo vetëm si një term matematikor. Një fraktal mund të quhet një objekt që ka të paktën një nga vetitë e mëposhtme:

Ka një strukturë jo të parëndësishme në të gjitha shkallët. Kjo është në kontrast me figurat e rregullta (të tilla si një rreth, elips, grafik i një funksioni të lëmuar): nëse merrni parasysh një fragment të vogël të një figure të rregullt në një shkallë shumë të madhe, ai do të duket si një fragment i një vije të drejtë. Për një fraktal, rritja e shkallës nuk çon në një thjeshtim të strukturës, domethënë, në të gjitha shkallët mund të shihni një pamje po aq komplekse.

Është i vetëngjashëm ose afërsisht i ngjashëm me veten.

Ka dimension metrikë të pjesshëm ose dimension metrikë që e kalon atë topologjik.Shumë objekte në natyrë kanë veti fraktale p.sh.: brigjet, retë, kurora pemësh, fjollat ​​e borës, sistemi i qarkullimit të gjakut, alveolat.

Dimensioni fraktal

Dimensioni fraktal(Dimensioni fraktal në anglisht) - një nga mënyrat për të përcaktuar dimensionin e një grupi në hapësirën metrike. Dimensioni fraktal n- grupi dimensional mund të përcaktohet duke përdorur formulën:

D = − lim ε → 0 ln ⁡ (N ε) ln ⁡ (ε) (\displaystyle D=-\lim \limits _(\varepsilon \në 0)(\frac (\ln(N_(\varepsilon ))) (\n(\varepsilon)))), Ku N ε (\displaystyle N_(\varepsilon ))- numri minimal n- "topa" dimensionale me rreze ε (\displaystyle \varepsilon), e nevojshme për të mbuluar kompletin.

Dimensioni fraktal mund të marrë një vlerë numerike jo të plotë.

Ideja bazë e dimensionit të thyer ka një histori të gjatë në fushën e matematikës, por ishte vetë termi që u krijua nga Benoit Mandelbrot në vitin 1967 në artikullin e tij mbi vetëngjashmërinë, në të cilin ai përshkroi dimensionin fraksional. Në këtë artikull, Mandelbrot iu referua punës së mëparshme nga Lewis Fry Richardson duke përshkruar idenë kundërintuitive se gjatësia e matur e një vije bregdetare varet nga gjatësia e një shkopi matës (shih Figurën 1). Sipas kësaj ideje, dimensioni fraktal i vijës bregdetare korrespondon me raportin e numrit të poleve (në një shkallë të caktuar) të nevojshme për të matur gjatësinë e vijës bregdetare me shkallën e zgjedhur të polit. Ekzistojnë disa përkufizime formale matematikore [⇨] të dimensionit fraktal që bazohen në këtë koncept bazë të një ndryshimi në një element me një ndryshim në shkallë.

Një shembull elementar është dimensioni fraktal i flokeve të dëborës Koch. Dimensioni i tij topologjik është 1, por nuk është aspak një kurbë e korrigjueshme, pasi gjatësia e lakores midis çdo dy pikash të një flok dëbore Koch është pafundësi. Asnjë pjesë e një kurbë, sado e vogël, nuk është një segment i drejtë. Përkundrazi, bora e Koch përbëhet nga një numër i pafund segmentesh të lidhura në kënde të ndryshme. Dimensioni fraktal i një lakore mund të shpjegohet në mënyrë intuitive duke sugjeruar se një linjë fraktal është një objekt shumë i detajuar (i detajuar) për të qenë njëdimensional, por jo mjaft kompleks për të qenë dydimensional. Prandaj, dimensioni i tij përshkruhet më mirë jo nga dimensioni i zakonshëm topologjik 1, por nga dimensioni i tij fraktal, i barabartë në këtë rast me një numër që shtrihet në intervalin midis 1 dhe 2.

Arti fraktal

Arti fraktal është një formë e artit algoritmik i krijuar duke llogaritur objektet fraktale dhe duke paraqitur rezultatet e llogaritjeve si imazhe statike, animacione dhe skedarë mediash të krijuar automatikisht. Arti fraktal filloi në mesin e viteve 1980. Është një zhanër i artit kompjuterik dhe artit dixhital që është pjesë e artit të mediave të reja. Në të njëjtën kohë, arti fraktal është një nga fushat e të ashtuquajturit "art shkencor".

Arti fraktal rrallëherë krijohet me dorë. Zakonisht krijohet në mënyrë indirekte nga softueri që gjeneron fraktale përmes tre hapave: vendosja e parametrave të softuerit fraktal përkatës; kryerja e llogaritjeve ndoshta të gjata; dhe vlerësimet e produktit. Në disa raste, programe të tjera grafike përdoren për të përpunuar më tej imazhet e krijuara. Imazhet jo-fraktale gjithashtu mund të përfshihen në një vepër arti. Seti Julia dhe grupi Mandelbrot konsiderohen ikona të artit fraktal.

Karakteristikat
Fraktalet më të thjeshta

Për ta marrë atë, duhet të merrni një trekëndësh (barabrinjës) me brendësi, të vizatoni vija të mesme në të dhe të hidhni atë qendror nga katër trekëndëshat e vegjël të formuar. Pastaj ju duhet të përsërisni të njëjtat hapa me secilin nga tre trekëndëshat e mbetur, etj. Fotografia tregon tre hapat e parë, dhe në demonstrimin flash mund të praktikoni dhe të merrni hapa deri në të dhjetën.

Hedhja e trekëndëshave qendrorë nuk është mënyra e vetme për të përfunduar me një trekëndësh të Sierpinskit. Ju mund të lëvizni "në drejtim të kundërt": merrni një trekëndësh fillimisht "bosh", më pas plotësoni trekëndëshin e formuar nga vijat e mesme në të, pastaj bëni të njëjtën gjë në secilin nga tre trekëndëshat e këndit, etj. Fillimisht, figurat do të të jenë shumë të ndryshme, por me rritjen e numrit të përsëritjeve, ato do të ngjajnë gjithnjë e më shumë me njëra-tjetrën dhe në kufi do të përkojnë.

Mënyra tjetër për të marrë një trekëndësh Sierpinski është edhe më e ngjashme me skemën e zakonshme për ndërtimin e fraktaleve gjeometrike duke zëvendësuar pjesë të përsëritjes së ardhshme me një fragment të shkallëzuar. Këtu, në çdo hap, segmentet që përbëjnë vijën e thyer zëvendësohen me një vijë të thyer prej tre lidhjesh (vetë është marrë në përsëritjen e parë). Ju duhet ta vendosni këtë vijë të thyer në mënyrë alternative në të djathtë dhe më pas në të majtë. Mund të shihet se tashmë përsëritja e tetë është shumë afër fraktalit dhe sa më tej të shkojë, aq më afër vijës do t'i afrohet.

Por kjo nuk është e gjitha. Rezulton se trekëndëshi i Sierpinskit është marrë si rezultat i një prej varieteteve të ecjes së rastësishme të një pike në një aeroplan. Kjo metodë quhet "loja e kaosit". Me ndihmën e tij mund të ndërtoni disa fraktale të tjera.

Thelbi i "lojës" është ky. Një trekëndësh i rregullt është i fiksuar në një aeroplan A 1 A 2 A 3. Shënoni çdo pikënisje B 0 . Pastaj zgjidhni rastësisht një nga tre kulmet e trekëndëshit dhe shënoni pikën B 1 - mesi i një segmenti me skajet në këtë kulm dhe në B 0 (në figurën në të djathtë, kulmi u zgjodh rastësisht A 1). E njëjta gjë përsëritet me një pikë B 1 për të marrë B 2. Pastaj ata marrin pikët B 3 , B 4, etj. Është e rëndësishme që pika të "kërcejë" në mënyrë të rastësishme, domethënë që çdo herë kulmi i trekëndëshit të zgjidhet rastësisht, pavarësisht se çfarë është zgjedhur në hapat e mëparshëm. Është e mahnitshme që nëse shënoni pika nga një sekuencë B i, atëherë së shpejti do të fillojë të shfaqet trekëndëshi i Sierpinskit. Më poshtë është se çfarë ndodh kur shënohen 100, 500 dhe 2500 pikë.

Disa prona

Opsione

Tapet (katror, ​​pecetë) nga Sierpinski. Versioni katror u përshkrua nga Wacław Sierpinski në 1916. Ai arriti të provojë se çdo kurbë që mund të vizatohet në një rrafsh pa vetëkryqëzime është homeomorfike për disa nënbashkësi të këtij katrori vrimash. Ashtu si një trekëndësh, një katror mund të bëhet nga dizajne të ndryshme. Në të djathtë është metoda klasike: ndarja e katrorit në 9 pjesë dhe hedhja e pjesës qendrore. Më pas e njëjta gjë përsëritet për 8 katrorët e mbetur etj.

Ashtu si një trekëndësh, një katror ka sipërfaqe zero. Dimensioni fraktal i një tapeti Sierpinski është i barabartë me log 3 8, i llogaritur në mënyrë të ngjashme me dimensionin e një trekëndëshi.

Piramida e Sierpinskit. Një nga analogët tredimensionale të trekëndëshit të Sierpinskit. Është ndërtuar në mënyrë të ngjashme, duke marrë parasysh tredimensionalitetin e asaj që po ndodh: 5 kopje të piramidës fillestare, të ngjeshura dy herë, përbëjnë përsëritjen e parë, 5 kopjet e saj do të përbëjnë përsëritjen e dytë, etj. Fraktali dimensioni është i barabartë me log 2 5. Shifra ka vëllim zero (në çdo hap gjysma e vëllimit hidhet jashtë), por në të njëjtën kohë sipërfaqja ruhet nga përsëritja në përsëritje, dhe për fraktalin është e njëjtë si për piramida fillestare.

Sfungjeri i Mengerit. Përgjithësimi i tapetit Sierpinski në hapësirën tredimensionale. Për të ndërtuar një sfungjer, ju duhet një përsëritje e pafund e procedurës: secili prej kubeve që përbëjnë përsëritjen ndahet në 27 kube tre herë më të vegjël, nga të cilët hidhet ai qendror dhe 6 fqinjët e tij. Domethënë, çdo kub gjeneron 20 të reja, tre herë më të vogla. Prandaj, dimensioni fraktal është log 3 20. Ky fraktal është një kurbë universale: çdo kurbë në hapësirën tredimensionale është homeomorfike për një nëngrup të sfungjerit. Sfungjeri ka volum zero (pasi në çdo hap shumëzohet me 20/27), por ka një sipërfaqe pafundësisht të madhe.

L
Linja Oman:

N - numri i segmenteve, madhësia A.

D - "shkalla e përkuljes"

N=(1/a)D; S=N*a ; S=(1/a)D-1

TE
Riva Koch

2) N=4L=1/3S(4)=4/3

N=16 L=1/9S(16)=16/9

Dimensioni fraktal:

D=lg4 /lg3=1,26…

Dimensioni fraktal i një grupi

Vëllimi i fraktalit në të hapësira e ngulitjesështë gjithmonë zero. Megjithatë, mund të jetë jo zero në një hapësirë ​​me dimension më të ulët. Për të përcaktuar dimensionin e kësaj hapësire D, le të thyejmë gjithçka n-hapësirë ​​dimensionale në kubikë të vegjël me gjatësi buzë ε dhe vëllimi ε n- Fig. 1. Le N(ε ) është numri minimal i kubeve që së bashku mbulojnë plotësisht grupin fraktal, pastaj sipas përkufizimit

Ekzistenca e këtij kufiri do të thotë se vëllimi i fraktalit është i kufizuar në D-hapësirë ​​dimensionale: me të vogla ε

dhe ndryshe nga dimensioni i zakonshëm D mund të jetë një vlerë thyesore, e cila është ajo që është më shpesh për grupet fraktale.

Natyrisht, për grupet e zakonshme ky përkufizim çon në rezultate të njohura. Pra, për turmën N pikat e izoluara kemi N(ε ) =N dhe për këtë arsye

Për një segment, një vijë e lëmuar gjatësie është e mjaftueshme L:N(ε ) =L/ε dhe për këtë arsye D= 1. Për sitin S sipërfaqe dydimensionale: N(ε ) =S/ε 2 dhe D= 2, etj.

Algoritmi rekurziv për ndërtimin e fraktaleve konstruktive.

1. Trekëndëshi i Sierpinskit

Trekëndëshi i Sierpinskit

Trekëndëshi i Sierpinskit- një fraktal, një nga analogët dydimensionale të grupit Cantor të propozuar nga matematikani polak Sierpinski në 1915. I njohur gjithashtu si "rrjeti" ose "pecetë" e Sierpinskit.

Ndërtimi

Merret një trekëndësh barabrinjës i ngurtë dhe në hapin e parë pjesa e brendshme e trekëndëshit të mesit hiqet nga qendra. Në hapin e dytë, tre trekëndëshat e mesëm hiqen nga tre trekëndëshat e mbetur, etj. Pas përsëritjes së pafund të kësaj procedure, mbetet një nëngrup i trekëndëshit të ngurtë - trekëndëshi Sierpinski.

Ndërtimi i trekëndëshit të Sierpinskit

Trekëndëshi i Sierpinskit gjithashtu mund të merret duke përdorur algoritmin e mëposhtëm:

Merrni tre pika në aeroplan dhe vizatoni një trekëndësh.

Zgjidhni rastësisht çdo pikë brenda trekëndëshit dhe lëvizni gjysmën e distancës nga kjo pikë në ndonjë nga tre kulmet e trekëndëshit.

Shënoni pozicionin aktual.

Përsëriteni nga hapi 2.

Konceptet e gjeometrisë fractal dhe fractal, të cilat u shfaqën në fund të viteve '70, janë vendosur fort midis matematikanëve dhe programuesve që nga mesi i viteve '80. Fjala fractal rrjedh nga latinishtja fractus dhe do të thotë që përbëhet nga fragmente. Ai u propozua nga Benoit Mandelbrot në 1975 për t'iu referuar strukturave të parregullta, por të ngjashme me të cilat ai ishte i shqetësuar. Lindja e gjeometrisë fraktal zakonisht lidhet me botimin e librit të Mandelbrot "The Fractal Geometria of Nature" në 1977. Punimet e tij përdorën rezultatet shkencore të shkencëtarëve të tjerë që punuan në periudhën 1875-1925 në të njëjtën fushë (Poincaré, Fatou, Julia, Cantor, Hausdorff Por vetëm në kohën tonë ka qenë e mundur të kombinojmë punën e tyre në një sistem të vetëm.
Roli i fraktaleve në grafikën kompjuterike sot është mjaft i madh. Ata vijnë në shpëtim, për shembull, kur është e nevojshme, duke përdorur disa koeficientë, për të përcaktuar linjat dhe sipërfaqet e formave shumë komplekse. Nga pikëpamja e grafikës kompjuterike, gjeometria fraktale është e domosdoshme kur krijohen re artificiale, male dhe sipërfaqe deti. Në fakt, është gjetur një mënyrë për të përfaqësuar lehtësisht objekte komplekse jo-Euklidiane, imazhet e të cilave janë shumë të ngjashme me ato natyrore.
Një nga vetitë kryesore të fraktaleve është vetëngjashmëria. Në rastin më të thjeshtë, një pjesë e vogël e një fraktali përmban informacion për të gjithë fraktalin. Përkufizimi i Mandelbrot për një fraktal është: "Një fraktal është një strukturë e përbërë nga pjesë që janë në njëfarë kuptimi të ngjashme me të tërën."

Ekziston një numër i madh i objekteve matematikore të quajtura fraktale (trekëndëshi i Sierpinskit, fjolla e borës Koch, kurba Peano, grupi Mandelbrot dhe tërheqës të Lorencit). Fraktalet përshkruajnë me saktësi të madhe shumë dukuri fizike dhe formacione të botës reale: malet, retë, rrjedhat e turbullta (vorbulla), rrënjët, degët dhe gjethet e pemëve, enët e gjakut, gjë që nuk i përgjigjet figurave të thjeshta gjeometrike. Për herë të parë, Benoit Mandelbrot foli për natyrën fraktale të botës sonë në veprën e tij kryesore "Gjeometria Fraktale e Natyrës".
Termi fractal u prezantua nga Benoit Mandelbrot në vitin 1977 në veprën e tij themelore Fractals, Form, Chaos and Dimension. Sipas Mandelbrot, fjala fractal vjen nga fjalët latine fractus - fraksionale dhe frangere - për të thyer, gjë që pasqyron thelbin e një fractal si një grup "i thyer", i parregullt.

Klasifikimi i fraktaleve.

Për atë Për të paraqitur të gjithë larminë e fraktaleve, është e përshtatshme të drejtoheni në klasifikimin e tyre të pranuar përgjithësisht. Ekzistojnë tre klasa fraktalesh.

1. Fraktale gjeometrike.

Fraktalet e kësaj klase janë më vizuale. Në rastin dy-dimensional, ato merren duke përdorur një vijë të thyer (ose sipërfaqe në rastin tredimensional), të quajtur gjenerator. Në një hap të algoritmit, secili nga segmentet që përbëjnë vijën e thyer zëvendësohet me poliline-gjenerator në një shkallë të përshtatshme. Si rezultat i përsëritjes së pafund të kësaj procedure, fitohet një fraktal gjeometrik.

Le të shohim një shembull të një prej këtyre objekteve fraktal - kurbës triadike Koch.

Ndërtimi i lakores triadike Koch.

Le të marrim një segment të drejtë me gjatësi 1. Le ta quajmë atë farë. E ndajmë farën në tre pjesë të barabarta 1/3 e gjatë, e hedhim pjesën e mesme dhe e zëvendësojmë me një vijë të thyer prej dy hallkash 1/3 e gjatë.

Ne do të marrim një vijë të thyer të përbërë nga 4 lidhje me një gjatësi totale prej 4/3, kështu që ne thërrasim gjenerata e parë.

Për të kaluar në gjeneratën e ardhshme të kurbës Koch, është e nevojshme të hidhni dhe zëvendësoni pjesën e mesme të secilës lidhje. Prandaj, gjatësia e gjeneratës së dytë do të jetë 16/9, e treta - 64/27. nëse vazhdojmë këtë proces deri në pafundësi, rezultati është një kurbë Koch triadike.

Le të shqyrtojmë tani vetitë e kurbës triadike Koch dhe të zbulojmë pse fraktalet quheshin "përbindësh".

Së pari, kjo kurbë nuk ka gjatësi - siç e kemi parë, me numrin e gjeneratave gjatësia e saj priret në pafundësi.

Së dyti, është e pamundur të ndërtohet një tangjente me këtë kurbë - secila nga pikat e saj është një pikë lakimi në të cilën derivati ​​nuk ekziston - kjo kurbë nuk është e qetë.

Gjatësia dhe butësia janë vetitë themelore të kthesave, të cilat studiohen si nga gjeometria Euklidiane ashtu edhe nga gjeometria e Lobachevsky dhe Riemann. Metodat tradicionale të analizës gjeometrike rezultuan të pazbatueshme për kurbën triadike Koch, kështu që kurba Koch doli të ishte një përbindësh - një "përbindësh" midis banorëve të lëmuar të gjeometrive tradicionale.

Ndërtimi i "dragoit" Harter-Haithway.

Për të marrë një objekt tjetër fraktal, duhet të ndryshoni rregullat e ndërtimit. Le të jetë elementi formues dy segmente të barabarta të lidhura në kënde të drejta. Në gjeneratën zero zëvendësoni segmentin e njësisë me ky element formues në mënyrë që këndi të jetë në krye. Mund të themi se me një zëvendësim të tillë ka një zhvendosje të mesit të lidhjes. Gjatë ndërtimit të gjeneratave të mëvonshme, ndiqet rregulli: lidhja e parë në të majtë zëvendësohet me një element formues në mënyrë që mesi i lidhjes të zhvendoset në të majtë të drejtimit të lëvizjes, dhe kur zëvendësohen lidhjet pasuese, drejtimet e zhvendosja e meseve të segmenteve duhet të alternohet. Figura tregon gjeneratat e para dhe gjeneratën e 11-të të kurbës të ndërtuar sipas parimit të përshkruar më sipër. Një kurbë me n që tenton në pafundësi quhet dragoi Harter-Haithaway.
Në grafikën kompjuterike, përdorimi i fraktaleve gjeometrike është i nevojshëm kur merren imazhe të pemëve dhe shkurreve. Fraktalet gjeometrike dydimensionale përdoren për të krijuar tekstura tre-dimensionale (modele në sipërfaqen e një objekti).

2.Fraktalet algjebrike

Ky është grupi më i madh i fraktaleve. Ato përftohen duke përdorur procese jolineare në hapësira n-dimensionale. Proceset dydimensionale janë më të studiuarat. Kur interpretohet një proces iterativ jolinear si një sistem dinamik diskret, mund të përdoret terminologjia e teorisë së këtyre sistemeve: portreti fazor, procesi i gjendjes së qëndrueshme, tërheqës, etj.
Dihet se sistemet dinamike jolineare kanë disa gjendje të qëndrueshme. Gjendja në të cilën sistemi dinamik gjendet pas një numri të caktuar përsëritjesh varet nga gjendja e tij fillestare. Prandaj, çdo gjendje e qëndrueshme (ose, siç thonë ata, tërheqës) ka një rajon të caktuar të gjendjeve fillestare, nga të cilat sistemi do të bjerë domosdoshmërisht në gjendjet përfundimtare në shqyrtim. Kështu, hapësira fazore e sistemit ndahet në zona të tërheqjes së tërheqësve. Nëse hapësira fazore është një hapësirë ​​dydimensionale, atëherë duke ngjyrosur zonat e tërheqjes me ngjyra të ndryshme, mund të merret një portret fazor me ngjyra i këtij sistemi (procesi përsëritës). Duke ndryshuar algoritmin e përzgjedhjes së ngjyrave, mund të merrni modele komplekse fraktal me modele të çuditshme shumëngjyrësh. Një surprizë për matematikanët ishte aftësia për të gjeneruar struktura shumë komplekse jo të parëndësishme duke përdorur algoritme primitive.

Kompleti Mandelbrot.

Si shembull, merrni parasysh grupin Mandelbrot. Algoritmi për ndërtimin e tij është mjaft i thjeshtë dhe bazohet në një shprehje të thjeshtë përsëritëse: Z = Z * Z + C, Ku Zi Dhe C- variabla komplekse. Përsëritjet kryhen për secilën pikë fillestare nga një rajon drejtkëndor ose katror - një nëngrup i planit kompleks. Procesi përsëritës vazhdon deri në Z nuk do të shkojë përtej rrethit të rrezes 2, qendra e të cilit shtrihet në pikën (0,0), (kjo do të thotë se tërheqësi i sistemit dinamik është në pafundësi), ose pas një numri mjaft të madh përsëritjesh (për shembull , 200-500) Z do të konvergojnë në një pikë të rrethit. Në varësi të numrit të përsëritjeve gjatë të cilave Z mbetur brenda rrethit, ju mund të vendosni ngjyrën e pikës C(Nëse Z mbetet brenda rrethit për një numër mjaft të madh përsëritjesh, procesi i përsëritjes ndalet dhe kjo pikë raster lyhet me ngjyrë të zezë).

3. Fraktale stokastike

Një klasë tjetër e njohur e fraktaleve janë fraktale stokastike, të cilat fitohen nëse disa nga parametrat e tij ndryshohen rastësisht në një proces iterativ. Në këtë rast, objektet që rezultojnë janë shumë të ngjashme me ato natyrore - pemët asimetrike, vijat bregdetare të thyer, etj. Fraktalet stokastike dydimensionale përdoren në modelimin e terrenit dhe sipërfaqes së detit.
Ekzistojnë klasifikime të tjera të fraktaleve, për shembull, ndarja e fraktaleve në deterministe (algjebrike dhe gjeometrike) dhe jo-përcaktuese (stokastike).

Rreth përdorimit të fraktaleve

Para së gjithash, fraktalet janë një fushë e artit të mahnitshëm matematikor, kur me ndihmën e formulave dhe algoritmeve më të thjeshta, fitohen fotografi me bukuri dhe kompleksitet të jashtëzakonshëm! Gjethet, pemët dhe lulet janë shpesh të dukshme në konturet e imazheve të ndërtuara.

Disa nga aplikimet më të fuqishme të fraktaleve qëndrojnë në grafikën kompjuterike. Së pari, ky është kompresim fraktal i imazheve dhe së dyti, ndërtimi i peizazheve, pemëve, bimëve dhe gjenerimi i teksturave fraktal. Fizika dhe mekanika moderne sapo kanë filluar të studiojnë sjelljen e objekteve fraktale. Dhe, sigurisht, fraktalet përdoren drejtpërdrejt në vetë matematikën.
Përparësitë e algoritmeve të kompresimit të imazhit fraktal janë madhësia shumë e vogël e skedarit të paketuar dhe koha e shkurtër e rikuperimit të imazhit. Imazhet e mbushura me fraktale mund të shkallëzohen pa shkaktuar pikselim. Por procesi i kompresimit zgjat shumë dhe ndonjëherë zgjat me orë të tëra. Algoritmi i paketimit me humbje fractal ju lejon të vendosni raportin e kompresimit, të ngjashëm me formatin jpeg. Algoritmi bazohet në kërkimin e pjesëve të mëdha të imazhit që janë të ngjashme me disa pjesë të vogla. Dhe vetëm cila pjesë është e ngjashme me të cilën është shkruar në skedarin e daljes. Gjatë ngjeshjes, zakonisht përdoret një rrjet katror (pjesët janë katrore), gjë që çon në një këndshmëri të lehtë gjatë rivendosjes së imazhit; një rrjet gjashtëkëndor nuk e ka këtë pengesë.
Iterated ka zhvilluar një format të ri imazhi, "Sting", i cili kombinon kompresimin fractal dhe "valë" (siç është jpeg) pa humbje. Formati i ri ju lejon të krijoni imazhe me mundësinë e shkallëzimit të mëvonshëm me cilësi të lartë, dhe vëllimi i skedarëve grafikë është 15-20% e vëllimit të imazheve të pakompresuara.
Tendenca e fraktaleve për t'iu ngjasuar maleve, luleve dhe pemëve është shfrytëzuar nga disa redaktorë grafikë, për shembull, retë fraktale nga studio 3D MAX, male fraktale në World Builder. Pemët fraktale, malet dhe peizazhet e tëra përcaktohen me formula të thjeshta, janë të lehta për t'u programuar dhe nuk ndahen në trekëndësha dhe kube të veçantë kur afrohen.
Nuk mund të injorohet përdorimi i fraktaleve në vetë matematikën. Në teorinë e grupeve, grupi Cantor provon ekzistencën e grupeve të dendura të përsosura askund; në teorinë e masës, funksioni i vetë-afinës "Shkallët e Cantorit" është një shembull i mirë i një funksioni shpërndarjeje të një mase njëjës.
Në mekanikë dhe fizikë, fraktalet përdoren për shkak të vetive unike të përsëritjes së skicave të shumë objekteve natyrore. Fraktalet ju lejojnë të përafroni pemët, sipërfaqet malore dhe çarjet me saktësi më të lartë se përafrimi duke përdorur grupe segmentesh ose poligonesh (me të njëjtën sasi të dhënash të ruajtura). Modelet fraktale, si objektet natyrore, kanë një "vrazhdësi" dhe kjo veti ruhet sado e madhe të jetë zmadhimi i modelit. Prania e një mase uniforme në fraktale lejon që dikush të aplikojë integrimin, teorinë e potencialit dhe t'i përdorë ato në vend të objekteve standarde në ekuacionet e studiuara tashmë.
Me një qasje fraktal, kaosi pushon së qeni çrregullim blu dhe fiton një strukturë të imët. Shkenca fraktale është ende shumë e re dhe ka një të ardhme të madhe përpara. Bukuria e fraktaleve është larg të qenit i shterur dhe do të na japë akoma shumë kryevepra - ato që kënaqin syrin dhe ato që sjellin kënaqësi të vërtetë në mendje.

Rreth ndërtimit të fraktaleve

Metoda e përafrimit të njëpasnjëshme

Duke parë këtë foto, nuk është e vështirë të kuptosh se si mund të ndërtosh një fraktal të ngjashëm (në këtë rast, piramidën Sierpinski). Duhet të marrim një piramidë të rregullt (tetraedron), më pas të presim mesin e saj (oktaedrin), duke rezultuar në katër piramida të vogla. Me secilën prej tyre kryejmë të njëjtin operacion, etj. Ky është një shpjegim disi naiv, por i qartë.

Le të shqyrtojmë thelbin e metodës më rreptësisht. Le të ketë një sistem IFS, d.m.th. sistemi i hartës së kompresimit S=(S 1,...,S m ) S i:R n ->R n (për shembull, për piramidën tonë pasqyrimet duken si S i (x)=1/2*x+o i , ku o i janë kulmet e tetraedrit, i=1,..,4). Pastaj zgjedhim një grup kompakt A 1 në R n (në rastin tonë zgjedhim një katërkëndor). Dhe ne përcaktojmë me induksion sekuencën e bashkësive A k:A k+1 =S 1 (A k ) U...U S m (A k ). Dihet se grupet A k me k në rritje e përafrojnë gjithnjë e më mirë tërheqësin e dëshiruar të sistemit S.

Vini re se secili nga këto përsëritje është një tërheqës sistemi i përsëritur i funksioneve të përsëritura(Termi anglisht Digrafi IFS, RIFS dhe gjithashtu I drejtuar nga grafiku IFS) dhe për këtë arsye ato janë të lehta për t'u ndërtuar duke përdorur programin tonë.

Metoda pikë për pikë ose probabiliste

Kjo është mënyra më e lehtë për t'u zbatuar në një kompjuter. Për thjeshtësi, ne konsiderojmë rastin e një grupi të sheshtë vetë-afine. Pra, le të jetë (S 1,..,S m) një sistem i kontraktimeve afine. Hartëzimi S i paraqitet në formën: S i (x)=A i (x-o i)+o i, ku A i është një matricë fikse me madhësi 2x2 dhe o i është një vektor kolone dydimensionale.

· Le të marrim pikën fikse të hartës së parë S 1 si pikënisje:
x: = o1;
Këtu përfitojmë nga fakti se të gjitha pikat fikse të shtypjes S 1 ,..,S m i përkasin fraktalit. Mund të zgjidhni një pikë arbitrare si pikënisje dhe sekuenca e pikave të krijuara prej saj do të tërhiqet në një fraktal, por më pas do të shfaqen disa pika shtesë në ekran.

· Le të shënojmë pikën aktuale x= (x 1 , x 2) në ekran:
putpixel(x 1,x 2,15);

· Le të zgjedhim rastësisht një numër j nga 1 në m dhe të rillogaritim koordinatat e pikës x:
j:=Random (m)+1;
x:=S j (x);

· Shkojmë në hapin 2, ose, nëse kemi bërë një numër mjaft të madh përsëritjesh, ndalojmë.
Shënim. Nëse raportet e kompresimit të pasqyrave S i janë të ndryshme, atëherë fraktali do të mbushet me pika në mënyrë të pabarabartë. Nëse pasqyrat S i janë të ngjashme, kjo mund të shmanget duke komplikuar pak algoritmin. Për ta bërë këtë, në hapin e tretë të algoritmit, numri j nga 1 në m duhet të zgjidhet me probabilitete p 1 =r 1 s,..,p m =r m s, ku r i shënojë koeficientët e kompresimit të pasqyrave Si, dhe numri s (i quajtur dimensioni i ngjashmërisë) gjendet nga ekuacioni r 1 s +...+r m s =1. Zgjidhja e këtij ekuacioni mund të gjendet, për shembull, me metodën e Njutonit.

Rreth fraktaleve dhe algoritmeve të tyre

Fractal vjen nga mbiemri latin "fractus", dhe në përkthim do të thotë i përbërë nga fragmente, dhe folja përkatëse latine "frangere" do të thotë të thyesh, domethënë të krijosh fragmente të parregullta. Konceptet e gjeometrisë fractal dhe fractal, të cilat u shfaqën në fund të viteve '70, janë vendosur fort midis matematikanëve dhe programuesve që nga mesi i viteve '80. Termi u krijua nga Benoit Mandelbrot në 1975 për t'iu referuar strukturave të parregullta por të ngjashme me të cilat ai ishte i shqetësuar. Lindja e gjeometrisë fraktal zakonisht shoqërohet me botimin e librit të Mandelbrot "The Fractal Geometria of Nature" në 1977. Punimet e tij përdorën rezultatet shkencore të shkencëtarëve të tjerë që punuan në periudhën 1875-1925 në të njëjtën fushë (Poincaré, Fatou, Julia, Cantor, Hausdorff).

Rregullimet

Më lejoni të bëj disa rregullime në algoritmet e propozuara në libër nga H.-O. Peitgen dhe P.H. Richter “The Beauty of Fractals” M. 1993 thjesht për të zhdukur gabimet e shtypit dhe për të lehtësuar kuptimin e proceseve pasi pas studimit të tyre shumë mbetën një mister për mua. Fatkeqësisht, këto algoritme "të kuptueshme" dhe "të thjeshta" udhëheqin një mënyrë jetese tronditëse.

Ndërtimi i fraktaleve bazohet në një funksion të caktuar jolinear të një procesi kompleks me reagim z = > z 2 +c pasi z dhe c -k janë numra kompleks, atëherë z = x + iy , c = p + iq është e nevojshme të zbërthejeni atë në x dhe y në mënyrë që të shkoni në një plan më realist për njeriun e zakonshëm:

x(k+1)=x(k) 2 -y(k) 2 + p,
y(k+1)=2*x(k)*y(k) + q.

Një plan i përbërë nga të gjitha çiftet (x,y ) mund të konsiderohet si për vlera fikse R dhe q, dhe me ato dinamike. Në rastin e parë, duke kaluar nëpër të gjitha pikat (x , y) aeroplanët dhe ngjyrosja e tyre në varësi të numrit të përsëritjeve të funksioneve të nevojshme për të dalë nga procesi përsëritës ose për mos ngjyrosjen e tyre (ngjyra e zezë) kur tejkalohen përsëritjet maksimale të lejueshme, marrim një hartë të grupit Julia. Nëse, përkundrazi, përcaktojmë çiftin fillestar të vlerave (x, y) dhe gjurmojmë fatin e tij koloristik me vlerat dinamike të ndryshimit të parametrave p dhe q, atëherë marrim imazhe të quajtura grupe Mandelbrot.

Për çështjen e algoritmeve për ngjyrosjen e fraktaleve.

Zakonisht trupi i një grupi përfaqësohet si një fushë e zezë, megjithëse është e qartë se ngjyra e zezë mund të zëvendësohet me ndonjë tjetër, por ky është gjithashtu një rezultat pak interesant. Marrja e një imazhi të një grupi të ngjyrosur me të gjitha ngjyrat është një detyrë që nuk mund të zgjidhet duke përdorur operacione ciklike sepse numri i përsëritjeve të grupeve që formojnë trupin është i barabartë me maksimumin e mundshëm dhe është gjithmonë i njëjtë. Është e mundur të ngjyrosni një grup me ngjyra të ndryshme duke përdorur rezultatin e kontrollit të gjendjes së daljes së ciklit (z_magnitude) ose diçka të ngjashme me të, por me operacione të tjera matematikore, si numër ngjyrash.

Aplikimi i një "mikroskopi fraktal"

për të demonstruar dukuritë kufitare.

Tërheqësit janë qendra që udhëheqin luftën për dominim në aeroplan. Një kufi shfaqet midis tërheqësve, duke përfaqësuar një model të lulëzuar. Duke rritur shkallën e shqyrtimit brenda kufijve të grupit, mund të merren modele jo të parëndësishme që pasqyrojnë gjendjen e kaosit determinist - një fenomen i zakonshëm në botën natyrore.

Objektet e studiuara nga gjeografët formojnë një sistem me kufij të organizuar shumë kompleks, dhe për këtë arsye identifikimi i tyre bëhet jo një detyrë e thjeshtë praktike. Komplekset natyrore kanë bërthama tipike që veprojnë si tërheqës që humbasin ndikimin e tyre në territor ndërsa ai largohet.

Duke përdorur një mikroskop fraktal për grupet Mandelbrot dhe Julia, mund të krijohet një ide e proceseve kufitare dhe dukurive që janë po aq komplekse, pavarësisht nga shkalla e shqyrtimit dhe në këtë mënyrë përgatitet perceptimi i specialistit për një takim me një objekt natyror dinamik dhe në dukje kaotik. në hapësirë ​​dhe kohë, për të kuptuar natyrën e gjeometrisë fraktal. Ngjyrat shumëngjyrëshe dhe muzika fraktal do të lënë padyshim një gjurmë të thellë në mendjet e studentëve.

Mijëra botime dhe burime të mëdha në internet u kushtohen fraktaleve, por për shumë specialistë larg shkencës kompjuterike, ky term duket krejtësisht i ri. Fraktalet, si objekte me interes për specialistët e fushave të ndryshme të dijes, duhet të zënë vendin e duhur në kurset e shkencave kompjuterike.

Shembuj

RRJETI SIEPINSKI

Ky është një nga fraktalet që Mandelbrot eksperimentoi kur zhvillonte konceptet e dimensioneve dhe përsëritjeve fraktal. Trekëndëshat e formuar nga lidhja e mesit të një trekëndëshi më të madh janë prerë nga trekëndëshi kryesor, duke formuar një trekëndësh me më shumë vrima. Në këtë rast, iniciatori është trekëndëshi i madh dhe shablloni është operacioni i prerjes së trekëndëshave të ngjashëm me atë më të madhin. Ju gjithashtu mund të merrni një version tre-dimensional të një trekëndëshi duke përdorur një katërkëndësh të zakonshëm dhe duke prerë katërkëndëshat e vegjël. Dimensioni i një fraktali të tillë është ln3/ln2 = 1.584962501. Për të marrë Tapeti Sierpinski, merrni një katror, ​​ndajeni në nëntë katrorë dhe prisni atë të mesit. Ne do të bëjmë të njëjtën gjë me pjesën tjetër, katrorët më të vegjël. Përfundimisht, formohet një rrjet fraktal i sheshtë, që nuk ka zonë, por me lidhje të pafundme. Në formën e tij hapësinore, sfungjeri Sierpinski shndërrohet në një sistem formash nga fundi në fund, në të cilin çdo element nga skaji në skaj zëvendësohet vazhdimisht nga lloji i tij. Kjo strukturë është shumë e ngjashme me një seksion të indit kockor. Një ditë struktura të tilla përsëritëse do të bëhen një element i strukturave të ndërtimit. Statika dhe dinamika e tyre, beson Mandelbrot, meritojnë një studim të ngushtë.

SIERPINSKI FRACTAL

Mos e ngatërroni këtë fraktal me rrjetën Sierpinski. Këto janë dy objekte krejtësisht të ndryshme. Në këtë fraktal, iniciatori dhe gjeneratori janë të njëjtë. Në çdo përsëritje, një kopje më e vogël e iniciatorit shtohet në çdo cep të gjeneratorit, e kështu me radhë. Nëse do të kryheshin një numër i pafund i përsëritjesh gjatë krijimit të këtij fraktal, ai do të zinte të gjithë rrafshin, pa lënë asnjë vrimë të vetme. Prandaj, dimensioni i tij fraktal është ln9/ln3 = 2.0.

KURVE KOCH

Kurba Koch është një nga fraktalet më tipike deterministe. Ajo u shpik në shekullin e nëntëmbëdhjetë nga një matematikan gjerman i quajtur Helge von Koch, i cili, duke studiuar veprën e Georg Kontor dhe Karl Weierstrasse, hasi në përshkrime të disa kthesave të çuditshme me sjellje të pazakontë. Iniciatori është një vijë e drejtë. Gjeneratori është një trekëndësh barabrinjës, anët e të cilit janë të barabarta me një të tretën e gjatësisë së segmentit më të madh. Këta trekëndësha shtohen në mes të secilit segment pa pushim. Në kërkimin e tij, Mandelbrot eksperimentoi gjerësisht me kthesat e Koch, dhe prodhoi figura të tilla si Ishujt Koch, Kryqet e Koch, Flokët e dëborës Koch dhe madje edhe paraqitjet tredimensionale të kurbës Koch duke përdorur një katërkëndor dhe duke shtuar katërkëndëshe më të vegjël në secilën prej faqeve të saj. Kurba Koch ka dimensionin ln4/ln3 = 1.261859507.

FRAKTALI MANDELBROT

Ky NUK është grupi Mandelbrot, të cilin e shihni mjaft shpesh. Kompleti Mandelbrot bazohet në ekuacione jolineare dhe është një fraktal kompleks. Ky është gjithashtu një variant i kurbës Koch, megjithëse ky objekt nuk është i ngjashëm me të. Iniciatori dhe gjeneratori janë gjithashtu të ndryshëm nga ato që përdoren për të krijuar fraktale bazuar në parimin e kurbës Koch, por ideja mbetet e njëjtë. Në vend që të bashkohen trekëndëshat barabrinjës me një segment kurbë, katrorët bashkohen me një katror. Për shkak të faktit se ky fraktal zë saktësisht gjysmën e hapësirës së caktuar në çdo përsëritje, ai ka një dimension të thjeshtë fraktal prej 3/2 = 1,5.

FRACTALS YLY DHE FLEKE DORËS

Të dyja këto objekte nuk janë fraktale klasike dhe nuk janë shpikur nga Mandelbrot apo ndonjë matematikan tjetër i famshëm. Unë thjesht i krijova këto fraktale për interes dhe për të eksperimentuar me programimin. Si iniciatori ashtu edhe gjeneratori këtu janë një figurë e formuar duke lidhur pikat e mesit të anëve me pikat e mesit të anëve të kundërta në një gjashtëkëndësh të rregullt. Për më tepër, unë mund të dyshoj vetëm për dimensionin e këtyre fraktaleve.

DARER PENTAGON

Një fraktal duket si një tufë pesëkëndëshash të shtrydhur së bashku. Në fakt, ai formohet duke përdorur një pesëkëndësh si iniciator dhe trekëndëshat izoscelorë në të cilët raporti i anës më të madhe me anën më të vogël është saktësisht i barabartë me të ashtuquajturin raport të artë (1.618033989 ose 1/(2cos72)) si gjenerator. . Këta trekëndësha priten nga mesi i çdo pesëkëndëshi, duke rezultuar në një formë që duket si 5 pesëkëndësha të vegjël të ngjitur në një të madh. Një variant i këtij fraktali mund të merret duke përdorur një gjashtëkëndësh si iniciator. Ky fraktal quhet Ylli i Davidit dhe është mjaft i ngjashëm me një version gjashtëkëndor të Flokës së dëborës Koch. Dimensioni fraktal i pesëkëndëshit Darer është ln6/ln (1+g), ku g është raporti i gjatësisë së anës më të madhe të trekëndëshit me gjatësinë e asaj më të vogël. Në këtë rast, g është raporti i artë, kështu që dimensioni fraktal është afërsisht 1.86171596. Dimensioni fraktal i Yllit të Davidit ln6/ln3 ose 1.630929754.

KORBA E HILBERTIT

Ky fraktal është shumë i ngjashëm me Fraktalin e Labirintit, me përjashtim të faktit se gjerësia e shkronjës U, e cila është gjeneratori, nuk ndryshon me çdo përsëritje. Sidoqoftë, ndryshe nga Fraktali i Labirintit, kurba e Hilbertit, e quajtur edhe Hotel Hilbert, ka një dimension të vetëm fraktal, që është saktësisht 2.0, pasi me një numër të pafund përsëritjesh, ajo do të zërë të gjithë rrafshin. fractal dhe më pas bëni të njëjtën gjë me një zonë të vogël të asaj zone, të dy zmadhimet do të jenë dukshëm të ndryshme nga njëra-tjetra. Dy imazhet do të jenë shumë të ngjashme në detaje, por nuk do të jenë plotësisht identike. Figura 1. Përafrimi i grupit Mandelbrot Krahasoni, për shembull, fotot e grupit Mandelbrot të paraqitura këtu, njëra prej të cilave është marrë duke zgjeruar një zonë të caktuar të tjetrës. Siç mund ta shihni, ato nuk janë absolutisht identike, megjithëse në të dyja shohim një rreth të zi, nga i cili tentakulat flakëruese shtrihen në drejtime të ndryshme. Këto elemente përsëriten pafundësisht në grupin Mandelbrot në përmasa në rënie. Fraktalet deterministike janë lineare, ndërsa fraktalet komplekse jo. Duke qenë jolineare, këto fraktale krijohen nga ato që Mandelbrot i quajti ekuacione algjebrike jolineare. Një shembull i mirë është procesi Zn+1=ZnI + C, i cili është ekuacioni i përdorur për të ndërtuar grupin Mandelbrot dhe Julia të shkallës së dytë. Zgjidhja e këtyre ekuacioneve matematikore përfshin numra kompleksë dhe imagjinarë. Kur ekuacioni interpretohet grafikisht në rrafshin kompleks, rezultati është një figurë e çuditshme në të cilën linjat e drejta bëhen kthesa dhe efektet e vetëngjashmërisë shfaqen, megjithëse jo pa deformime, në nivele të ndryshme të shkallës. Në të njëjtën kohë, e gjithë tabloja në tërësi është e paparashikueshme dhe shumë kaotike. Siç mund ta shihni duke parë fotot, fraktale komplekse janë me të vërtetë shumë komplekse dhe nuk mund të krijohen pa ndihmën e një kompjuteri. Për të marrë rezultate shumëngjyrëshe, ky kompjuter duhet të ketë një bashkëprocesor të fuqishëm matematikor dhe një monitor me rezolucion të lartë. Ndryshe nga fraktalet deterministe, fraktalet komplekse nuk llogariten në 5-10 përsëritje. Pothuajse çdo pikë në ekranin e kompjuterit është si një fraktal i veçantë. Gjatë përpunimit matematik, çdo pikë trajtohet si një vizatim i veçantë. Çdo pikë korrespondon me një vlerë specifike. Ekuacioni është ndërtuar për çdo pikë dhe kryhet, për shembull, 1000 përsëritje. Për të marrë një imazh relativisht të pashtrembëruar në një periudhë kohore të pranueshme për kompjuterët shtëpiak, është e mundur të kryhen 250 përsëritje për një pikë. Shumica e fraktaleve që shohim sot janë me ngjyra të bukura. Ndoshta imazhet fraktal fitojnë një rëndësi kaq të madhe estetike pikërisht për shkak të skemave të tyre të ngjyrave. Pasi të jetë llogaritur ekuacioni, kompjuteri analizon rezultatet. Nëse rezultatet mbeten të qëndrueshme, ose luhaten rreth një vlere të caktuar, pika zakonisht bëhet e zezë. Nëse vlera në një hap ose në një tjetër priret në pafundësi, pika është pikturuar me një ngjyrë të ndryshme, ndoshta blu ose të kuqe. Gjatë këtij procesi, kompjuteri cakton ngjyra për të gjitha shpejtësitë e lëvizjes. Në mënyrë tipike, pikat që lëvizin shpejt janë me ngjyrë të kuqe, ndërsa ato më të ngadalta janë me ngjyrë të verdhë, e kështu me radhë. Pikat e errëta janë ndoshta më të qëndrueshmet. Fraktalet komplekse janë të ndryshme nga përcaktuese në kuptimin që ato janë pafundësisht komplekse, por në të njëjtën kohë mund të gjenerohen nga një formulë shumë e thjeshtë. Fraktalet përcaktuese nuk kërkojnë formula ose ekuacione. Thjesht merrni pak letër vizatimi dhe mund të ndërtoni një sitë Sierpinski deri në 3 ose 4 përsëritje pa ndonjë vështirësi. Provojeni këtë me shumë Julia! Është më e lehtë për të matur gjatësinë e vijës bregdetare të Anglisë! SET MANDELBROT Fig 2. Kompleti Mandelbrot Kompletet Mandelbrot dhe Julia janë ndoshta dy më të zakonshmet midis fraktaleve komplekse. Ato mund të gjenden në shumë revista shkencore, kopertina librash, kartolina dhe mbrojtëse të ekranit kompjuterik. Kompleti Mandelbrot, i cili u ndërtua nga Benoit Mandelbrot, është ndoshta shoqata e parë që njerëzit kanë kur dëgjojnë fjalën fractal. Ky fraktal, i cili i ngjan një makinerie gërshetimi me zona të ndezura si pemë dhe rrethore të lidhura me të, krijohet nga formula e thjeshtë Zn+1=Zna+C, ku Z dhe C janë numra kompleks dhe a është një numër pozitiv. Seti Mandelbrot, i cili mund të shihet më shpesh, është grupi Mandelbrot i shkallës së dytë, domethënë a = 2. Fakti që grupi Mandelbrot nuk është vetëm Zn+1=ZnІ+C, por një fraktal, treguesi në formulën e të cilit mund të jetë çdo numër pozitiv, ka mashtruar shumë. Në këtë faqe ju shihni një shembull të grupit Mandelbrot për vlera të ndryshme të eksponentit a. Figura 3. Shfaqja e flluskave në a=3.5 Procesi Z=Z*tg (Z+C) është gjithashtu popullor. Duke përfshirë funksionin tangjentë, rezultati është një grup Mandelbrot i rrethuar nga një zonë që i ngjan një mollë. Kur përdorni funksionin kosinus, fitohen efektet e flluskave të ajrit. Me pak fjalë, ka një numër të pafund mënyrash për të konfiguruar grupin Mandelbrot për të prodhuar fotografi të ndryshme të bukura. SHUMË JULIA Çuditërisht, grupet Julia janë formuar duke përdorur të njëjtën formulë si grupi Mandelbrot. Seti Julia u shpik nga matematikani francez Gaston Julia, pas të cilit grupi u emërua. Pyetja e parë që lind pas një njohjeje vizuale me grupet Mandelbrot dhe Julia është "nëse të dy fraktalet krijohen sipas të njëjtës formulë, pse janë kaq të ndryshëm?" Shikoni së pari fotot e setit Julia. Mjaft e çuditshme, ka lloje të ndryshme të grupeve Julia. Kur vizatoni një fraktal duke përdorur pika të ndryshme fillestare (për të filluar procesin e përsëritjes), krijohen imazhe të ndryshme. Kjo vlen vetëm për grupin Julia. Figura 4. Seti Julia Edhe pse nuk mund të shihet në foto, një fraktal Mandelbrot është në fakt shumë fraktale Julia të lidhura së bashku. Çdo pikë (ose koordinatë) e grupit Mandelbrot korrespondon me një fraktal Julia. Kompletet Julia mund të gjenerohen duke përdorur këto pika si vlera fillestare në ekuacionin Z=ZI+C. Por kjo nuk do të thotë që nëse zgjidhni një pikë në fraktalin Mandelbrot dhe e zmadhoni atë, mund të merrni fraktalin Julia. Këto dy pika janë identike, por vetëm në një kuptim matematikor. Nëse e merrni këtë pikë dhe e llogaritni duke përdorur këtë formulë, mund të merrni fraktalin Julia, që korrespondon me një pikë të caktuar të fraktalit Mandelbrot.