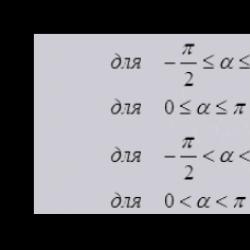The sin, cos, tg, and ctg functions are always accompanied by an arcsine, arccosine, arctangent, and arccotangent. One is a consequence of the other, and pairs of functions are equally important for working with trigonometric expressions.

Consider the drawing of a unit circle, which graphically displays the values ​​of trigonometric functions.

If you calculate arcs OA, arcos OC, arctg DE and arcctg MK, then they will all be equal to the value of the angle α. The formulas below reflect the relationship between the main trigonometric functions and their corresponding arcs.

To understand more about the properties of the arcsine, it is necessary to consider its function. Schedule has the form of an asymmetric curve passing through the center of coordinates.

Arcsine properties:

If we compare graphs sin And arc sin, two trigonometric functions can find common patterns.

Arc cosine

Arccos of the number a is the value of the angle α, the cosine of which is equal to a.

Curve y = arcos x mirrors the plot of arcsin x, with the only difference being that it passes through the point π/2 on the OY axis.

Consider the arccosine function in more detail:

1. The function is defined on the segment [-1; 1].
2. ODZ for arccos - .
3. The graph is entirely located in the I and II quarters, and the function itself is neither even nor odd.
4. Y = 0 for x = 1.
5. The curve decreases along its entire length. Some properties of the arc cosine are the same as the cosine function.

Some properties of the arc cosine are the same as the cosine function.

It is possible that such a “detailed” study of the “arches” will seem superfluous to schoolchildren. However, otherwise, some elementary typical USE tasks can lead students to a dead end.

Exercise 1. Specify the functions shown in the figure.

Answer: rice. 1 - 4, fig. 2 - 1.

In this example, the emphasis is on the little things. Usually, students are very inattentive to the construction of graphs and the appearance of functions. Indeed, why memorize the form of the curve, if it can always be built from calculated points. Do not forget that under test conditions, the time spent on drawing for a simple task will be required to solve more complex tasks.

Arctangent

Arctg the number a is such a value of the angle α that its tangent is equal to a.

If we consider the plot of the arc tangent, we can distinguish the following properties:

1. The graph is infinite and defined on the interval (- ∞; + ∞).
2. Arctangent is an odd function, therefore, arctan (- x) = - arctan x.
3. Y = 0 for x = 0.
4. The curve increases over the entire domain of definition.

Let's give a brief comparative analysis of tg x and arctg x in the form of a table.

Arc tangent

Arcctg of the number a - takes such a value of α from the interval (0; π) that its cotangent is equal to a.

Properties of the arc cotangent function:

1. The function definition interval is infinity.
2. The range of admissible values ​​is the interval (0; π).
3. F(x) is neither even nor odd.
4. Throughout its length, the graph of the function decreases.

Comparing ctg x and arctg x is very simple, you just need to draw two drawings and describe the behavior of the curves.

Task 2. Correlate the graph and the form of the function.

Logically, the graphs show that both functions are increasing. Therefore, both figures display some arctg function. It is known from the properties of the arc tangent that y=0 for x = 0,

Answer: rice. 1 - 1, fig. 2-4.

Trigonometric identities arcsin, arcos, arctg and arcctg

Previously, we have already identified the relationship between arches and the main functions of trigonometry. This dependence can be expressed by a number of formulas that allow expressing, for example, the sine of an argument through its arcsine, arccosine, or vice versa. Knowledge of such identities can be useful in solving specific examples.

There are also ratios for arctg and arcctg:

Another useful pair of formulas sets the value for the sum of the arcsin and arcos and arcctg and arcctg values ​​of the same angle.

Examples of problem solving

Trigonometry tasks can be conditionally divided into four groups: calculate the numerical value of a particular expression, plot a given function, find its domain of definition or ODZ, and perform analytical transformations to solve the example.

When solving the first type of tasks, it is necessary to adhere to the following action plan:

When working with graphs of functions, the main thing is the knowledge of their properties and the appearance of the curve. Tables of identities are needed to solve trigonometric equations and inequalities. The more formulas the student remembers, the easier it is to find the answer to the task.

Suppose in the exam it is necessary to find the answer for an equation of the type:

If you correctly transform the expression and bring it to the desired form, then solving it is very simple and fast. First, let's move arcsin x to the right side of the equation.

If we remember the formula arcsin (sinα) = α, then we can reduce the search for answers to solving a system of two equations:

The constraint on the model x arose, again from the properties of arcsin: ODZ for x [-1; 1]. When a ≠ 0, part of the system is a quadratic equation with roots x1 = 1 and x2 = - 1/a. With a = 0, x will be equal to 1.

This article is about finding the values ​​of the arcsine, arccosine, arctangent and arccotangent given number. First, we will clarify what is called the value of the arcsine, arccosine, arctangent and arccotangent. Next, we get the main values ​​​​of these arc functions, after which we will figure out how the values ​​\u200b\u200bof the arc sine, arc cosine, arc tangent and arc tangent are found from the tables of sines, cosines, tangents and cotangents of Bradys. Finally, let's talk about finding the arcsine of a number when the arccosine, arctangent or arccotangent of this number is known, etc.

Page navigation.

Values ​​for arcsine, arccosine, arctangent, and arccotangent

First, you need to figure out what is value of arcsine, arccosine, arctangent and arccotangent».

Tables of sines and cosines, as well as tangents and cotangents of Bradys, allow you to find the value of the arcsine, arccosine, arctangent and arccotangent of a positive number in degrees with an accuracy of one minute. It is worth mentioning here that finding the values ​​of the arcsine, arccosine, arctangent and arccotangent of negative numbers can be reduced to finding the values ​​of the corresponding arcfunctions of positive numbers by referring to the formulas arcsin, arccos, arctg and arcctg of opposite numbers of the form arcsin(−a)=−arcsin a , arccos (−a)=π−arccos a , arctg(−a)=−arctg a , and arcctg(−a)=π−arcctg a .

Let's deal with finding the values ​​of the arcsine, arccosine, arctangent and arccotangent using the Bradis tables. We will do this with examples.

Suppose we need to find the value of the arcsine 0.2857. We find this value in the table of sines (cases when this value is not in the table, we will analyze below). It corresponds to the sine of 16 degrees 36 minutes. Therefore, the desired value of the arcsine of the number 0.2857 is an angle of 16 degrees 36 minutes.

Often it is necessary to take into account the corrections from the three columns on the right of the table. For example, if we need to find the arcsine of 0.2863. According to the table of sines, this value is obtained as 0.2857 plus a correction of 0.0006, that is, the value of 0.2863 corresponds to a sine of 16 degrees 38 minutes (16 degrees 36 minutes plus 2 minutes of correction).

If the number whose arcsine is of interest to us is not in the table and cannot even be obtained, taking into account the corrections, then in the table you need to find the two values ​​\u200b\u200bof the sines closest to it, between which this number is enclosed. For example, we are looking for the value of the arcsine of the number 0.2861573 . This number is not in the table; with the help of amendments, this number cannot be obtained either. Then we find the two closest values ​​\u200b\u200bof 0.2860 and 0.2863, between which the original number is enclosed, these numbers correspond to the sines of 16 degrees 37 minutes and 16 degrees 38 minutes. The desired value of the arcsine 0.2861573 lies between them, that is, any of these angle values ​​can be taken as an approximate value of the arcsine with an accuracy of 1 minute.

The values ​​of the arc cosine, and the values ​​of the arc tangent and the values ​​of the arc cotangent are absolutely similar (in this case, of course, tables of cosines, tangents and cotangents are used, respectively).

Finding the value of arcsin through arccos, arctg, arcctg, etc.

For example, let's say we know that arcsin a=−π/12 , but we need to find the value of arccos a . We calculate the value of the arccosine we need: arccos a=π/2−arcsin a=π/2−(−π/12)=7π/12.

The situation is much more interesting when, from the known value of the arcsine or arccosine of the number a, it is required to find the value of the arctangent or arccotangent of this number a, or vice versa. Unfortunately, we do not know the formulas that define such relationships. How to be? Let's deal with this with an example.

Let us know that the arc cosine of the number a is equal to π / 10, and we need to calculate the value of the arc tangent of this number a. You can solve the problem as follows: find the number a from the known value of the arc cosine, and then find the arc tangent of this number. To do this, we first need a table of cosines, and then a table of tangents.

The angle π / 10 radians is an angle of 18 degrees, according to the table of cosines we find that the cosine of 18 degrees is approximately equal to 0.9511, then the number a in our example is 0.9511.

It remains to turn to the table of tangents, and with its help find the value of the arc tangent we need 0.9511, it is approximately equal to 43 degrees 34 minutes.

This topic is logically continued by the material of the article evaluate expressions containing arcsin, arccos, arctg, and arcctg.

Bibliography.

• Algebra: Proc. for 9 cells. avg. school / Yu. N. Makarychev, N. G. Mindyuk, K. I. Neshkov, S. B. Suvorova; Ed. S. A. Telyakovsky.- M.: Enlightenment, 1990.- 272 p.: Ill.- ISBN 5-09-002727-7
• Bashmakov M.I. Algebra and the beginning of analysis: Proc. for 10-11 cells. avg. school - 3rd ed. - M.: Enlightenment, 1993. - 351 p.: ill. - ISBN 5-09-004617-4.
• Algebra and the beginning of the analysis: Proc. for 10-11 cells. general education institutions / A. N. Kolmogorov, A. M. Abramov, Yu. P. Dudnitsyn and others; Ed. A. N. Kolmogorova.- 14th ed.- M.: Enlightenment, 2004.- 384 p.: ill.- ISBN 5-09-013651-3.
• I. V. Boikov, L. D. Romanova. Collection of tasks for preparing for the exam, part 1, Penza 2003.
• Bradis V. M. Four-digit mathematical tables: For general education. textbook establishments. - 2nd ed. - M.: Bustard, 1999.- 96 p.: ill. ISBN 5-7107-2667-2

Lesson and presentation on the topic: "Arc tangent. Arc tangent. Tables of arc tangent and arc tangent"

Additional materials
Dear users, do not forget to leave your comments, feedback, suggestions! All materials are checked by an antivirus program.

Manuals and simulators in the online store "Integral" from the company 1C
We solve problems in geometry. Interactive construction tasks for grades 7-10
We solve problems in geometry. Interactive tasks for building in space

What will we study:
1. What is arc tangent?
2. Definition of arc tangent.
3. What is the arc tangent?
4. Definition of arc tangent.
5. Tables of values.
6. Examples.

What is arctangent?

Guys, we have already learned how to solve equations for cosine and sine. Now let's learn how to solve similar equations for tangent and cotangent. Consider the equation tg(x)= 1. To solve this equation, we construct two graphs: y= 1 and y= tg(x). The graphs of our functions have an infinite number of intersection points. The abscissas of these points look like: x= x1 + πk, x1 is the abscissa of the point of intersection of the line y= 1 and the main branch of the function y= tg(x), (-π/2 <x1> π/2). For the number x1, the designation was introduced as the arc tangent. Then the solution of our equation will be written: x= arctg(1) + πk.

Definition of arc tangent

arctg(a) is such a number from the segment [-π/2; π/2], whose tangent is a.

The equation tg(x)= a has a solution: x= arctg(a) + πk, where k is an integer.

Also note: arctg(-a)= -arctg(a).

What is arc tangent?

Let's solve the equation сtg(x)=1. To do this, we will build two graphs: y=1 and y=сtg(x). The graphs of our functions have an infinite number of intersection points. The abscissas of these points look like: x= x1 + πk. x1 is the abscissa of the point of intersection of the line y= 1 and the main branch of the function y= сtg(x), (0 <x1> π).
For the number x1, the notation was introduced as the arc tangent. Then the solution of our equation will be written: x= arcсtg(1) + πk.

Definition of arc tangent

arcctg(a) is a number from the segment whose cotangent is equal to a.

The equation ctg(x)= a has a solution: x= arcctg(a) + πk, where k is an integer.

Also note: arcctg(-a)= π - arcctg(a).

Tables of values ​​of arc tangent and arc tangent

Table of tangent and cotangent values

Table of values ​​of arctangent and arccotangent

Examples

1. Calculate: arctg(-√3/3).
Solution: Let arctg(-√3/3)= x, then tg(x)= -√3/3. By definition –π/2 ≤x≤ π/2. Let's look at the values ​​of the tangent in the table: x= -π/6, because tg(-π/6)= -√3/3 and – π/2 ≤ -π/6 ≤ π/2.
Answer: arctg(-√3/3)= -π/6.

2. Calculate: arctg(1).
Solution: Let arctg(1)= x, then tg(x)= 1. By definition –π/2 ≤ x ≤ π/2. Let's look at the values ​​of the tangent in the table: x= π/4, because tg(π/4)= 1 and – π/2 ≤ π/4 ≤ π/2.
Answer: arctg(1)= π/4.

3. Calculate: arcctg(√3/3).
Solution: Let arcctg(√3/3)= x, then ctg(x)= √3/3. By definition, 0 ≤ x ≤ π. Let's look at the values ​​of the cotangent in the table: x= π/3, because ctg(π/3)= √3/3 and 0 ≤ π/3 ≤ π.
Answer: arcctg(√3/3) = π/3.

4. Calculate: arcctg(0).
Solution: Let arcctg(0)= x, then ctg(x) = 0. By definition, 0 ≤ x ≤ π. Let's look at the values ​​of the cotangent in the table: x= π/2, because ctg(π/2)= 0 and 0 ≤ π/2 ≤ π.
Answer: arcctg(0) = π/2.

5. Solve the equation: tg(x)= -√3/3.
Solution: Let's use the definition and get: x= arctg(-√3/3) + πk. Let's use the formula arctg(-a)= -arctg(a): arctg(-√3/3)= – arctg(√3/3)= – π/6; then x= – π/6 + πk.
Answer: x= = - π/6 + πk.

6. Solve the equation: tg(x)= 0.
Solution: Let's use the definition and get: x= arctg(0) + πk. arctan(0)= 0, we substitute the solution into the formula: x= 0 + πk.
Answer: x= πk.

7. Solve the equation: tg(x) = 1.5.
Solution: Let's use the definition and get: x= arctg(1.5) + πk. There is no arctangent value for this value in the table, then we will leave the answer in this form.
Answer: x= arctg(1.5) + πk.

8. Solve the equation: ctg(x)= -√3/3.
Solution: Let's use the formula: ctg(x)= 1/tg(x); ctg(x)= -√3/3 =1/tg(x) => tg(x)= -√3. Let's use the definition and get: x= arctg (-√3) + πk. arctg(-√3)= –arctg(√3)= –π/3, then x= -π/3 + πk.
Answer: x= - π/3 + πk.

9. Solve the equation: ctg(x)= 0.
Solution: Let's use the formula: ctg(x)= cos(x)/sin(x). Then we need to find the values ​​of x for which cos(x)=0, we get that x= π/2+ πk.
Answer: x= π/2 + πk.

10. Solve the equation: ctg(x)= 2.
Solution: Let's use the definition and get: x= arcсtg(2) + πk. There is no arc tangent value for this value in the table, then we will leave the answer in this form. Answer: x= arctg(2) + πk.

Tasks for independent solution

What is arcsine, arccosine? What is arc tangent, arc tangent?

Attention!
There are additional
material in Special Section 555.
For those who strongly "not very..."
And for those who "very much...")

To concepts arcsine, arccosine, arctangent, arccotangent the student population is wary. He does not understand these terms and, therefore, does not trust this glorious family.) But in vain. These are very simple concepts. Which, by the way, make life much easier for a knowledgeable person when solving trigonometric equations!

Confused about simplicity? In vain.) Right here and now you will be convinced of this.

Of course, for understanding, it would be nice to know what sine, cosine, tangent and cotangent are. Yes, their table values ​​for some angles ... At least in the most general terms. Then there will be no problems here either.

So, we are surprised, but remember: arcsine, arccosine, arctangent and arctangent are just some angles. No more, no less. There is an angle, say 30°. And there is an angle arcsin0.4. Or arctg(-1.3). There are all kinds of angles.) You can simply write angles in different ways. You can write the angle in degrees or radians. Or you can - through its sine, cosine, tangent and cotangent ...

What does the expression mean

arcsin 0.4?

This is the angle whose sine is 0.4! Yes Yes. This is the meaning of the arcsine. I repeat specifically: arcsin 0.4 is an angle whose sine is 0.4.

And that's it.

To keep this simple thought in my head for a long time, I will even give a breakdown of this terrible term - arcsine:

arc sin 0,4
corner, whose sine equals 0.4

As it is written, so it is heard.) Almost. Console arc means arc(word arch know?), because ancient people used arcs instead of corners, but this does not change the essence of the matter. Remember this elementary decoding of a mathematical term! Moreover, for the arc cosine, arc tangent and arc tangent, the decoding differs only in the name of the function.

What is arccos 0.8?
This is an angle whose cosine is 0.8.

What is arctan(-1,3) ?
This is an angle whose tangent is -1.3.

What is arcctg 12 ?
This is an angle whose cotangent is 12.

Such an elementary decoding allows, by the way, to avoid epic blunders.) For example, the expression arccos1,8 looks quite solid. Let's start decoding: arccos1,8 is an angle whose cosine is equal to 1.8... Hop-hop!? 1.8!? Cosine cannot be greater than one!

Right. The expression arccos1,8 does not make sense. And writing such an expression in some answer will greatly amuse the verifier.)

Elementary, as you can see.) Each angle has its own personal sine and cosine. And almost everyone has their own tangent and cotangent. Therefore, knowing the trigonometric function, you can write down the angle itself. For this, arcsines, arccosines, arctangents and arccotangents are intended. Further, I will call this whole family a diminutive - arches. to type less.)

Attention! Elementary verbal and conscious deciphering the arches allows you to calmly and confidently solve a variety of tasks. And in unusual tasks only she saves.

Is it possible to switch from arches to ordinary degrees or radians?- I hear a cautious question.)

Why not!? Easily. You can go there and back. Moreover, it is sometimes necessary to do so. Arches are a simple thing, but without them it’s somehow calmer, right?)

For example: what is arcsin 0.5?

Let's look at the decryption: arcsin 0.5 is the angle whose sine is 0.5. Now turn on your head (or Google)) and remember which angle has a sine of 0.5? The sine is 0.5 y angle of 30 degrees. That's all there is to it: arcsin 0.5 is a 30° angle. You can safely write:

arcsin 0.5 = 30°

Or, more solidly, in terms of radians:

That's it, you can forget about the arcsine and work on with the usual degrees or radians.

If you realized what is arcsine, arccosine ... What is arctangent, arccotangent ... Then you can easily deal with, for example, such a monster.)

An ignorant person will recoil in horror, yes ...) And a knowledgeable remember the decryption: the arcsine is the angle whose sine is ... Well, and so on. If a knowledgeable person also knows the table of sines ... The table of cosines. A table of tangents and cotangents, then there are no problems at all!

It is enough to consider that:

I will decipher, i.e. translate the formula into words: angle whose tangent is 1 (arctg1) is a 45° angle. Or, which is the same, Pi/4. Similarly:

and that's all... We replace all the arches with values ​​in radians, everything is reduced, it remains to calculate how much 1 + 1 will be. It will be 2.) Which is the correct answer.

This is how you can (and should) move from arcsines, arccosines, arctangents and arctangents to ordinary degrees and radians. This greatly simplifies scary examples!

Often, in such examples, inside the arches are negative values. Like, arctg(-1.3), or, for example, arccos(-0.8)... It's not a problem. Here are some simple formulas for going from negative to positive:

You need, say, to determine the value of an expression:

You can solve this using a trigonometric circle, but you don't want to draw it. Well, okay. Going from negative values ​​inside the arc cosine to positive according to the second formula:

Inside the arccosine on the right already positive meaning. What

you just have to know. It remains to substitute the radians instead of the arc cosine and calculate the answer:

That's all.

Restrictions on arcsine, arccosine, arctangent, arccotangent.

Is there a problem with examples 7 - 9? Well, yes, there is some trick there.)

All of these examples, from 1st to 9th, are carefully sorted out on the shelves in Section 555. What, how and why. With all the secret traps and tricks. Plus ways to dramatically simplify the solution. By the way, this section contains a lot of useful information and practical tips on trigonometry in general. And not only in trigonometry. Helps a lot.

If you like this site...

By the way, I have a couple more interesting sites for you.)

You can practice solving examples and find out your level. Testing with instant verification. Learning - with interest!)

you can get acquainted with functions and derivatives.