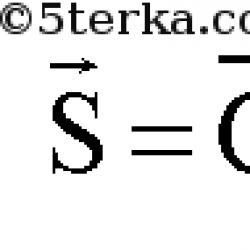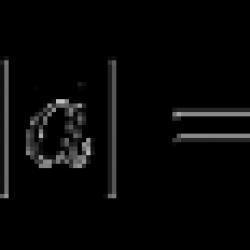Let's find the length of the vector by its coordinates (in a rectangular coordinate system), by the coordinates of the points of the beginning and end of the vector, and by the cosine theorem (2 vectors and the angle between them are given).

Vector is a directed line segment. The length of this segment determines the numerical value of the vector and is called vector length or vector modulus.

1. Calculating the length of a vector from its coordinates

If the vector coordinates are given in a flat (two-dimensional) rectangular coordinate system, i.e. a x and a y are known, then the length of the vector can be found by the formula

In the case of a vector in space, a third coordinate is added

In MS EXCEL expression =ROOT(SUMSQ(B8:B9)) allows you to calculate the modulus of the vector (it is assumed that the vector coordinators are entered in the cells B8:B9, see example file ).

The SUMSQ() function returns the sum of the squares of the arguments, i.e. in this case, equivalent to the formula =B8*B8+B9*B9 .

The example file also calculates the length of the vector in space.

An alternative formula is the expression =ROOT(SUMPRODUCT(B8:B9,B8:B9)).

2. Finding the length of a vector through the coordinates of points

If the vector is given through the coordinates of its start and end points, then the formula will be different =ROOT(SUMDIFF(C28:C29,B28:B29))

The formula assumes that the coordinates of the start and end points are entered in the ranges C28:C29 And B28:B29 respectively.

Function SUMMQVAR() in Returns the sum of the squared differences of the corresponding values ​​in two arrays.

In fact, the formula first calculates the coordinates of the vector (the difference between the corresponding coordinates of the points), then calculates the sum of their squares.

3. Finding the length of a vector using the cosine theorem

If you want to find the length of a vector using the cosine theorem, then 2 vectors are usually given (their modules and the angle between them).

Find the length of the vector with using the formula =ROOT(SUMQ(B43:C43)-2*B43*C43*COS(B45))

In cells B43:B43 contains the lengths of the vectors a and b, and the cell B45 - the angle between them in radians (in fractions of the number PI() ).

If the angle is given in degrees, then the formula will be slightly different. =ROOT(B43*B43+C43*C43-2*B43*C43*COS(B46*PI()/180))

Note: for clarity, in a cell with an angle value in degrees, you can use , see, for example, the article

vector modulus- the magnitude of the vector - [L.G. Sumenko. English Russian Dictionary of Information Technologies. M .: GP TsNIIS, 2003.] Topics information technology in general Synonyms vector value EN absolute value of a vector ...

vector modulus- vektoriaus modulis statusas T sritis fizika atitikmenys: angl. absolute value of vector vok. Vectorbetrag, m rus. vector length, f; vector modulus, m pranc. module d’un vecteur, m … Fizikos terminų žodynas

- (from Latin modulus "small measure"): Wiktionary has an article "modulus" Mo ... Wikipedia

Module (from Latin modulus "small measure") is a component, separable or at least mentally separated from the general. A modular thing is usually called a thing consisting of clearly defined parts, which can often be removed or added without destroying the thing ... ... Wikipedia

The absolute value or modulus of a real or complex number x is the distance from x to the origin. More precisely: The absolute value of a real number x is a non-negative number denoted by |x| and defined as follows: ... ... Wikipedia

wave vector modulus- - [L.G. Sumenko. English Russian Dictionary of Information Technologies. M .: GP TsNIIS, 2003.] Topics information technology in general EN magnitude of propagation vector ... Technical Translator's Handbook

envelope code vector convolver module- - [L.G. Sumenko. English Russian Dictionary of Information Technologies. M.: GP TsNIIS, 2003.] Topics information technology in general EN shape codevector convolution module ... Technical Translator's Handbook

The modulus of a complex number is the length of the vector corresponding to this number: . The modulus of a complex number z is usually denoted by | z | or r. Let and be real numbers such that a complex number (usual notation). Then Numbers ... Wikipedia

Module in mathematics, 1) M. (or absolute value) of a complex number z = x + iy is the number ═ (the root is taken with a plus sign). When representing a complex number z in trigonometric form z \u003d r (cos j + i sin j), the real number r is ... ... Great Soviet Encyclopedia

Abelian group with an operator ring. M. is a generalization of a (linear) vector space over a field K for the case when K is replaced by some ring. Let a ring A be given. The additive Abelian group Mnas. left A module, if defined... ... Mathematical Encyclopedia

Characterized by magnitude and direction. For example, in geometry and in the natural sciences, a vector is a directed line segment in Euclidean space (or on a plane).

It is one of the fundamental concepts of linear algebra. When using the most general definition, vectors turn out to be almost all objects studied in linear algebra, including matrices, tensors, however, if these objects are present in the surrounding context, a vector is understood, respectively, as a row vector or a column vector, a tensor of the first rank. The properties of operations on vectors are studied in vector calculus.

Notation [ | ]

The vector represented by the set n (\displaystyle n) elements (component) a 1 , a 2 , … , a n (\displaystyle a_(1),a_(2),\ldots ,a_(n)) denoted in the following ways:

To emphasize that it is a vector (and not a scalar), use an overline, overhead arrow, bold or gothic font:

Vector addition is almost always denoted by a plus sign:

Multiplication by a number is simply written next to it, without a special sign, for example:

and the number is usually written on the left.

There are no generally accepted vector designations; bold type, a dash or arrow above a letter, the Gothic alphabet, etc. are used.

In geometry [ | ]

In geometry, vectors are understood as directed segments. This interpretation is often used in computer graphics when building lightmaps using surface normals. You can also use vectors to find the areas of various shapes, such as triangles and parallelograms, as well as the volumes of bodies: tetrahedron and parallelepiped.
Sometimes a direction is identified with a vector.

A vector in geometry is naturally associated with transfer (parallel transfer), which obviously clarifies the origin of its name (lat. vector, carrier). Indeed, any directed segment uniquely defines some kind of parallel translation of a plane or space, and vice versa, a parallel translation uniquely defines a single directed segment (unambiguously - if we consider all directed segments of the same direction and length to be equal - that is, consider them as free vectors) .

The interpretation of a vector as a translation allows us to introduce the operation of vector addition in a natural and intuitively obvious way - as a composition (successive application) of two (or several) translations; the same applies to the operation of multiplying a vector by a number.

In linear algebra[ | ]

General definition[ | ]

The most general definition of a vector is given by means of general algebra:

• Denote F (\displaystyle (\mathfrak (F)))(Gothic F) some field with many elements F (\displaystyle F), additive operation + (\displaystyle +), multiplicative operation ∗ (\displaystyle*), and the corresponding neutral elements : additive unit and multiplicative unit 1 (\displaystyle 1).
• Denote V (\displaystyle (\mathfrak (V)))(Gothic V) some Abelian group with a set of elements V (\displaystyle V), additive operation + (\displaystyle +) and, accordingly, with the additive unit 0 (\displaystyle\mathbf(0) ).

In other words, let F = ⟨F; + , ∗ ⟩ (\displaystyle (\mathfrak (F))=\langle F;+,*\rangle ) And V = ⟨V; + ⟩ (\displaystyle (\mathfrak (V))=\langle V;+\rangle ).

If there is an operation F × V → V (\displaystyle F\times V\to V), such that for any a , b ∈ F (\displaystyle a,b\in F) and for any x , y ∈ V (\displaystyle \mathbf (x) ,\mathbf (y) \in V) the following relations are fulfilled:

Vector as a sequence[ | ]

Vector- (sequence, tuple) homogeneous elements. This is the most general definition in the sense that there may be no conventional vector operations given at all, there may be fewer of them, or they may not satisfy the usual linear space axioms. It is in this form that a vector is understood in programming, where, as a rule, it is denoted by an identifier name with square brackets (for example, object). The list of properties models the accepted in

The length of the vector a → will be denoted by a → . This notation is similar to the modulus of a number, so the length of a vector is also called the modulus of a vector.

To find the length of a vector on the plane by its coordinates, it is required to consider a rectangular Cartesian coordinate system O x y . Let it contain some vector a → with coordinates a x ; a y . We introduce a formula for finding the length (modulus) of the vector a → in terms of the coordinates a x and a y .

Set aside the vector O A → = a → from the origin. Let's define the corresponding projections of the point A onto the coordinate axes as A x and A y . Now consider a rectangle O A x A A y with diagonal O A .

From the Pythagorean theorem follows the equality O A 2 = O A x 2 + O A y 2 , whence O A = O A x 2 + O A y 2 . From the already known definition of the coordinates of a vector in a rectangular Cartesian coordinate system, we obtain that O A x 2 = a x 2 and O A y 2 = a y 2 , and by construction, the length of O A is equal to the length of the vector O A → , therefore, O A → = O A x 2 + O A y 2.

Hence it turns out that formula for finding the length of a vector a → = a x ; a y has the corresponding form: a → = a x 2 + a y 2 .

If the vector a → is given as an expansion in coordinate vectors a → = a x i → + a y j → , then its length can be calculated using the same formula a → = a x 2 + a y 2 , in this case the coefficients a x and a y are as the coordinates of the vector a → in the given coordinate system.

Example 1

Calculate the length of the vector a → = 7 ; e , given in a rectangular coordinate system.

Solution

To find the length of a vector, we will use the formula for finding the length of a vector by coordinates a → = a x 2 + a y 2: a → = 7 2 + e 2 = 49 + e

Answer: a → = 49 + e .

Formula for finding the length of a vector a → = a x ; a y ; a z by its coordinates in the Cartesian coordinate system Oxyz in space, is derived similarly to the formula for the case on the plane (see figure below)

In this case, O A 2 \u003d O A x 2 + O A y 2 + O A z 2 (since OA is the diagonal of a rectangular parallelepiped), hence O A \u003d O A x 2 + O A y 2 + O A z 2. From the definition of the coordinates of the vector, we can write the following equalities O A x = a x ; O A y = a y ; O A z = a z ; , and the length of OA is equal to the length of the vector we are looking for, therefore, O A → = O A x 2 + O A y 2 + O A z 2 .

It follows that the length of the vector a → = a x ; a y ; a z is equal to a → = a x 2 + a y 2 + a z 2 .

Example 2

Calculate the length of the vector a → = 4 i → - 3 j → + 5 k → , where i → , j → , k → are the unit vectors of the rectangular coordinate system.

Solution

Given a decomposition of a vector a → = 4 · i → - 3 · j → + 5 · k → , its coordinates are a → = 4 , - 3 , 5 . Using the formula above, we get a → = a x 2 + a y 2 + a z 2 = 4 2 + (- 3) 2 + 5 2 = 5 2 .

Answer: a → = 5 2 .

The length of a vector in terms of the coordinates of its start and end points

Above, formulas were derived that allow you to find the length of a vector by its coordinates. We have considered cases on the plane and in three-dimensional space. Let's use them to find the coordinates of the vector by the coordinates of its start and end points.

So, given points with given coordinates A (a x; a y) and B (b x; b y), hence the vector A B → has coordinates (b x - a x; b y - a y), which means that its length can be determined by the formula: A B → = ( b x - a x) 2 + (b y - a y) 2

And if points with given coordinates A (a x; a y; a z) and B (b x; b y; b z) in three-dimensional space are given, then the length of the vector A B → can be calculated by the formula

A B → = (b x - a x) 2 + (b y - a y) 2 + (b z - a z) 2

Example 3

Find the length of the vector A B → if in a rectangular coordinate system A 1 , 3 , B - 3 , 1 .

Solution

Using the formula for finding the vector length from the coordinates of the start and end points on the plane, we get A B → = (b x - a x) 2 + (b y - a y) 2: A B → = (- 3 - 1) 2 + (1 - 3) 2 = 20 - 2 3 .

The second solution implies the application of these formulas in turn: A B → = (- 3 - 1; 1 - 3) = (- 4; 1 - 3) ; A B → = (- 4) 2 + (1 - 3) 2 = 20 - 2 3 . -

Answer: A B → = 20 - 2 3 .

Example 4

Determine for what values ​​the length of the vector A B → equals 30 if A (0 , 1 , 2) ; B (5 , 2 , λ 2) .

Solution

First, let's write the length of the vector A B → according to the formula: A B → = (b x - a x) 2 + (b y - a y) 2 + (b z - a z) 2 = (5 - 0) 2 + (2 - 1) 2 + (λ 2 - 2) 2 = 26 + (λ 2 - 2) 2

Then we equate the resulting expression to 30, from here we find the desired λ:

26 + (λ 2 - 2) 2 = 30 26 + (λ 2 - 2) 2 = 30 (λ 2 - 2) 2 = 4 λ 2 - 2 = 2 and l and λ 2 - 2 = - 2 λ 1 = - 2 , λ 2 = 2 , λ 3 = 0 .

Answer: λ 1 \u003d - 2, λ 2 \u003d 2, λ 3 \u003d 0.

Finding the length of a vector using the law of cosines

Alas, the coordinates of a vector are not always known in tasks, so let's consider other ways to find the length of a vector.

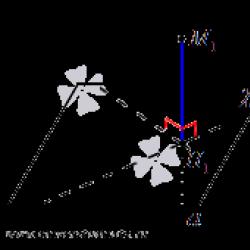
Let the lengths of two vectors A B → , A C → and the angle between them (or the cosine of the angle) be given, and it is required to find the length of the vector B C → or C B → . In this case, you should use the cosine theorem in the triangle △ A B C , calculate the length of the side B C , which is equal to the desired length of the vector.

Let's consider such a case in the following example.

Example 5

The lengths of the vectors A B → and A C → are equal to 3 and 7, respectively, and the angle between them is equal to π 3 . Calculate the length of the vector B C → .

Solution

The length of the vector B C → in this case is equal to the length of the side B C of the triangle △ A B C . The lengths of the sides A B and A C of the triangle are known from the condition (they are equal to the lengths of the corresponding vectors), the angle between them is also known, so we can use the cosine theorem: B C 2 = A B 2 + A C 2 - 2 A B A C cos ∠ (A B , → A C →) = 3 2 + 7 2 - 2 3 7 cos π 3 = 37 ⇒ B C = 37 Thus, B C → = 37 .

Answer: B C → = 37 .

So, to find the length of a vector by coordinates, there are the following formulas a → = a x 2 + a y 2 or a → = a x 2 + a y 2 + a z 2, according to the coordinates of the points of the beginning and end of the vector A B → = (b x - a x) 2 + ( b y - a y) 2 or A B → = (b x - a x) 2 + (b y - a y) 2 + (b z - a z) 2, in some cases the cosine theorem should be used.

If you notice a mistake in the text, please highlight it and press Ctrl+Enter