При изменении числа частиц в системе и необходимая для описания свойств открытых систем (с перем. числом частиц).

X. п. m i i -го компонента многокомпонентной системы равен частной производной от любого из термодинамич. потенциалов по кол-ву (числу частиц) этого компонента при пост. значениях остальных термодинамич. переменных, определяющих данный термодинамич. потенциал, напр. m i = (дF/дN i) T,V,N (F -свободная энергия, Т -темп-ра, V -объём, j i ). Т. о., в системах с перем. числом частиц в выражение для дифференциала, напр. dF , следует добавить величину :

где р - давление, S -энтропия. Наиб. просто X. п. связан с термодинамич. потенциалом G (см. Гиббса энергия): . Для однокомпонентной системы X. п. m = G/N ,

т. е. представляет собой энергию Гиббса, отнесённую к одной частице. Вследствие аддитивности G , кроме давления и темп-ры, X. п. зависит только от концентраций отд. компонентов, но не от числа частиц в каждом компоненте. В простейшем случае идеальных газов m i зависит только от концентрации i -го компонента:

где -полное число частиц, m ~ i -X. п. чистого i -го

компонента. Часто величины m i удобно использовать в качестве независимых термодинамич. переменных вместо N i . В переменных Т, V , m i состояние системы характеризует термодинамич. потенциал

X. п. является термодинамич. параметром в большом каноническом распределении Гиббса для систем с перем. числом частиц. В качестве нормировочной постоянной X. п. входит в распределения Больцмана, Бозе - Эйнштейна и Ферми - Дирака для частиц идеальных газов (см. Статистическая физика ).В системах, к к-рым применима статистика Больцмана или Бозе - Эйнштейна, X. п. всегда отрицателен. Для ферми-газа X. п. при нулевой темп-ре положителен и определяет граничную ферми-энергию (см. Ферми-поверхность )и вырождения температуру . Если

полное число частиц в системе не фиксировано, а должно определяться из условия термодинамич. равновесия, как, напр., для фононов в твёрдом теле или для фотонов в случае равновесного теплового , то равновесие характеризуется равенством нулю X. п.

Понятие X. п. позволяет сформулировать условия равновесия термодинамического . Одно из условий состоит в том, что X. п. любого компонента одинаков в разл. фазах и в разных местах одной фазы. Это обусловлено возможностью перераспределения частиц, приводящего к выравниванию X. п. Для систем в пространственно неоднородном внеш. поле равновесие означает, что

где m i 0 - X. п. в отсутствие поля, U i (r) -потенц. энергия частиц i -го компонента во внеш. поле. Для газа в поле тяжести это условие приводит к барометрич. ф-ле для газа. В случае заряж. частиц в электрич. поле (напр., в полупроводниках) величину m i наз. э л е к т р о х им и ч е с к и м п о т е н ц и а л о м, оставляя название X. п. за m i 0 . Равенство значений X. п. для частиц одного компонента, находящихся в разных фазах, определяет условия равновесия при фазовых переходах (

Термодинамика фазовых переходов. Определения

Рассмотрим термодинамику систем, в которых могут иметь место фазовые переходы. Термодинамическая система, которая может обмениваться веществом с окружающей средой, называется открытой .

Термодинамическая система называется однородной или гомогенной , если в каждой малой её части физические свойства вещества и интенсивные термодинамические параметры одинаковы или меняются в пространстве непрерывным образом.

Термодинамические системы, в которых физические свойства вещества и интенсивные параметры меняются скачкообразно на некоторых поверхностях внутри системы, называются гетерогенными . Примером гетерогенной системы является кипящая жидкость.

Области в гетерогенной системе с однородными или непрерывно изменяющимися свойствами и параметрами называются фазами . При равновесии гетерогенной системы в отсутствие внешних полей интенсивные параметры в пределах каждой фазы постоянны.

Но в различных фазах эти интенсивные параметры не обязаны быть одинаковыми. Гомогенная система является, таким образом, однофазной.

Каждая из фаз в общем случае может представлять собой гомогенную смесь химически чистых веществ, между которыми возможны химические реакции. Химически чистые вещества в смеси называются компонентами . Фазы в общем случае могут обмениваться не только энергией в форме работы или теплоты, но и веществом. Превращение вещества из одного фазового состояния в другое называется фазовым переходом .

Пусть однокомпонентная однофазная ТД система является открытой, причём только вещество, составляющее систему, может проникать через оболочку. И пусть система является равновесной.

Изменение внутренней энергии такой системы будет происходить не только вследствие подвода теплоты и совершения над ней работы, но также и вследствие изменения её массы. Вещество, проникающее через оболочку, несёт присущую ему энергию. Тогда уравнения Гиббса для каждого из четырёх термодинамических потенциалов (5.3) и (5.5) следует дополнить ещё одним слагаемым, пропорциональным изменению массы системы, т.е.

Величина μ , определяемая частными производными

носит название химического потенциала и имеет смысл изменения энергии термодинамической системы при изменении её массы на единицу при поддержании постоянной той или иной пары независимых параметров системы.

Найдём связь химического потенциала с другими потенциалами системы. Для этого рассмотрим в (4.12) четвёртое из выражений. Свободную энергию Гиббса Φ, энтропию S и объём системы V запишем через их удельные величины:

Заменяя дифференциал свободной энергии Гиббса его выражением и перегруппировав слагаемые, получим:

Согласно (4.5) для M = const = 1 кг , откуда, ввиду произвольности дифференциала массы dM , находим:

т.е. химический потенциал вещества есть его удельная свободная энергия Гиббса.

4.6. Условия термодинамического равновесия многофазных систем . Правило фаз Гиббса

Рассмотрим однокомпонентную систему , состоящую из двух взаимодействующих фаз. Пусть каждая из фаз находится в своём внутреннем равновесии, т.е. каждая из них характеризуется своим набором параметров. Изучим вопрос о равновесии между фазами. Для этого заключим всю систему в изолирующую оболочку (рис.4.1). Тогда при малом изменении состояния каждой из фаз (подсистем) можно записать для них термодинамические тождества в соответствии с (4.1)

(4.15)

В силу аддитивности экстенсивных величин , замкнутости системы и обратимости процесса имеем

т.е. после суммирования равенств (4.5) получаем:

В силу произвольности дифференциалов , множители в скобках при этих дифференциалах должны быть равны нулю, откуда получаем условия термодинамического равновесия искомой системы:

(4.16)

Химический потенциал по определению сам является функцией естественной пары переменных , таким образом, условие равновесия фаз может быть записано в виде

Вид функций от T и p в общем случае различен для каждой из фаз, поэтому условие (4.17) не является тождеством. Это есть алгебраическое уравнение, связывающее температуру и давление в равновесной системе, состоящей из двух сосуществующих взаимодействующих фаз, между которыми имеет место обмен теплотой, работой и веществом.

Таким образом, в двухфазной однокомпонентной системе температура и давление однозначно связаны. Объём же системы может принимать произвольное значение в зависимости от соотношения между массами фаз. Состояние равновесия двухфазной системы называется состоянием насыщения, а равные для фаз температура и давление - параметрами насыщения T s , p s .

Рассмотрим равновесие трёхфазной однокомпонентной системы . В данном случае:

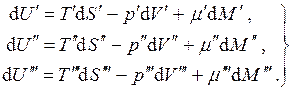(4.18)

Но для замкнутой системы:

с учётом чего, складывая уравнения (4.8), получаем:

Так как все дифференциалы здесь независимы и значения их произвольны, находим условия равновесия:

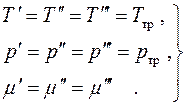(4.19)

Химическое равновесие, т.е. равенство химических потенциалов фаз, может быть записано в виде двух алгебраических уравнений

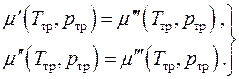(4.20)

Это есть система двух уравнений с двумя неизвестными . Равновесная однокомпонентная система может существовать одновременно в виде трёх фаз только при строго определённых значениях давления и температуры. Такое состояние системы называется тройной точкой .

Для равновесной четырёхфазной однокомпонентной системы:

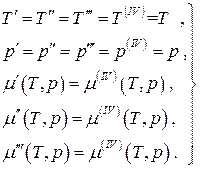(4.21)

систему трёх уравнений с двумя неизвестными. Такая система уравнений является несовместной за исключением случая, когда любые два из них пропорциональны друг другу, т.е. когда две из четырёх фаз фактически неразличимы, а это уже будет трёхфазная система. Таким образом, в равновесной однокомпонентной системе возможно одновременное сосуществование не более, чем трёх фаз. Если равновесная термодинамическая система является многокомпонентной, то число одновременно сосуществующих фаз может быть больше трёх, а именно

где n есть число компонентов системы. Этот результат носит название правила фаз Гиббса .

ПЛАН ЛЕКЦИИ:

1. Организационная часть лекции: принимается рапорт о готовности курсантов к занятию, отмечаются в журнале отсутствующие (время 3-5 мин.).

2. Введение к разделу «Тепломассообмен».

Вопросы лекции:

Механизмы теплопереноса.

· Температурное поле.

· Температурный градиент.

· Основной закон теплопроводности.

· Коэффициент теплопроводности.

· Дифференциальное уравнение теплопроводности.

· Краевые условия.

3. Заключение.

К следующему занятию курсанты должны:

ЗНАТЬ: дифференциальное уравнение теплопроводности; определения коэффициентов тепло- и температуропроводности.

УМЕТЬ: применять краевые условия при решении задач на уравнение Фурье.

ИМЕТЬ ПРЕДСТАВЛЕНИЕ: о механизмах переноса тепла в телах различного строения и агрегатного состояния.

4. Задания на самоподготовку:

_____________/ профессор каф. физики и теплообмена, д.ф.-м.н., П.В. Скрипов

Лекция рассмотрена и одобрена на заседании кафедры

Протокол №_______ от «_____»_____________ 2011 г.

Заведующий кафедрой физики и теплообмена

профессор, д.т.н. __________________ / Н.М. Барбин

«_____»______________ 2011 г.

Свободная энергия системы (энергия Гиббса G и энергия Гельмгольца F ) зависит от внешних условий:

Эта зависимость является полной для простейших систем, состоящих из одного компонента.

Термодинамическая система может состоять как из одного, так и из нескольких компонентов. Очевидно, что величина свободной энергии многокомпонентной системы будет зависеть как от внешних условий (Т , р , или V ), так и от природы и количества веществ, составляющих систему, т. е. свободная энергия, как и любая термодинамическая функция, является экстенсивным свойством системы. В случае, если состав системы изменяется во времени (т.е. в системе протекает химическая реакция), необходимо учесть влияние изменения состава на величину свободной энергии системы.

Рассмотрим термодинамическую систему, состоящую из k компонентов. Пусть n 1 , n 2 , …, n k – число моль 1-го, 2-го, …, k -го компонентов. Тогда свободная энергия Гиббса является функцией следующих переменных:

G = f (p , T , n 1 , n 2 , …, n k )

Продифференцируем по всем переменным:

(2.1)

Введем обозначение:

………………….

,

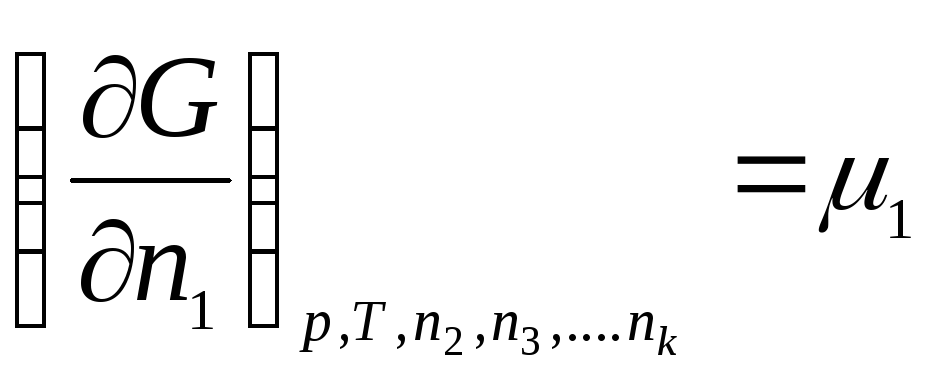
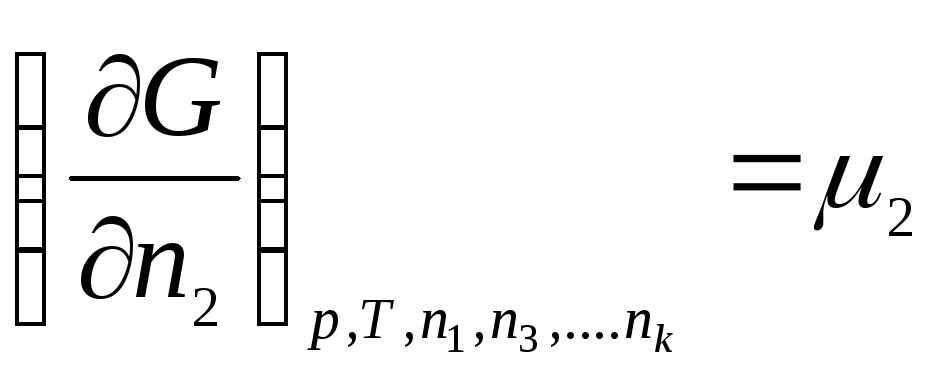
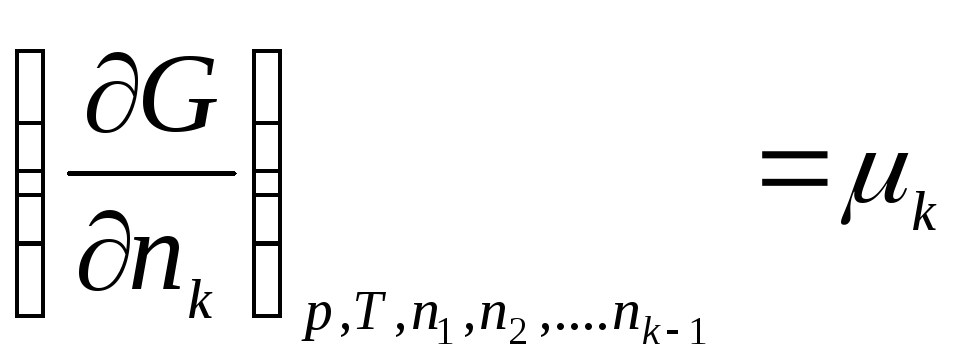где μ 1 , μ 2 , …, μ k – химические потенциалы 1-го, 2-го, …, k -го компонентов соответственно.

В общем виде

.

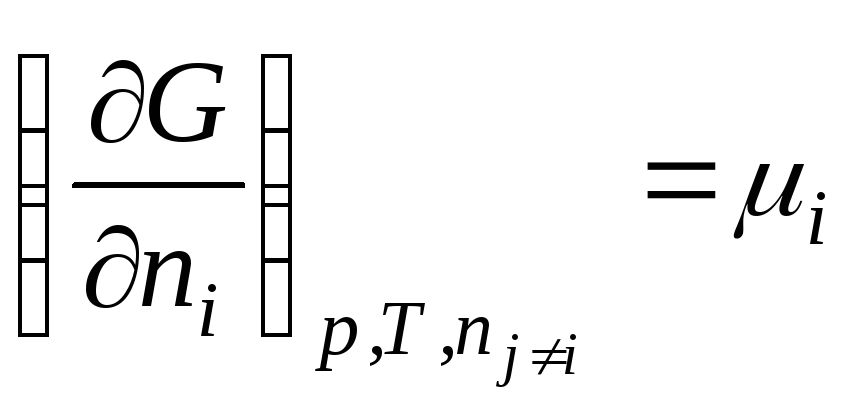Аналогичное выражение получаем для свободной энергии Гельмгольца:

F = f (V , T , n 1 , n 2 , …, n k )

.

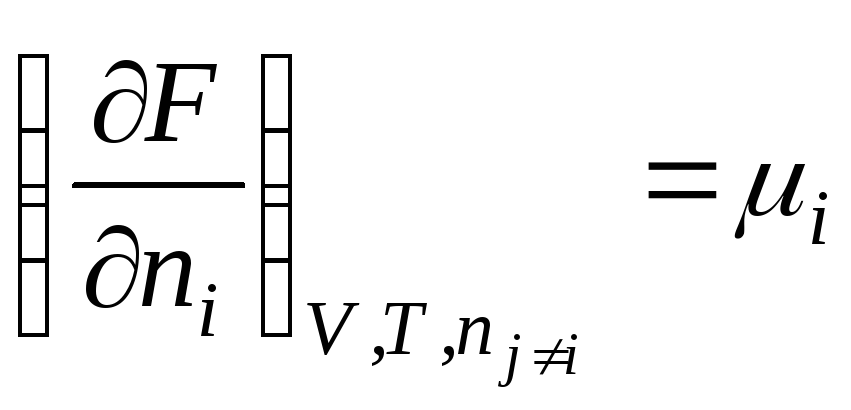Таким образом, химический потенциал – это частная производная от свободной энергии по количеству моль i -го компонента при постоянстве соответствующих внешних параметрах и числе моль всех остальных компонентов. Таким образом, химический потенциал является парциальной мольной энергией Гиббса (при р , Т = const ):

.

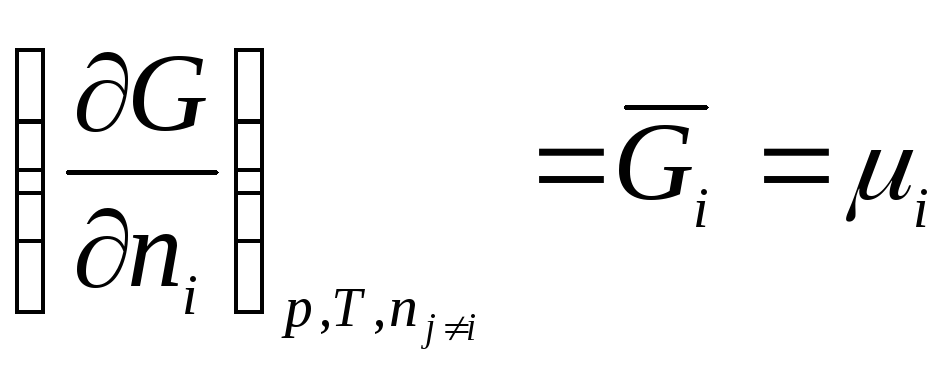Свободная энергия – это общее свойство системы, химический потенциал характеризует свойства отдельного компонента, входящего в систему. Химический потенциал является интенсивным свойством системы, т.к. не зависит от массы системы.

При р, Т = const уравнение (2.1) имеет вид:

. (2.2)

В этом случае изменение энергии Гиббса, то есть полезная работа системы, обусловлена только изменением состава системы в результате протекания химической реакции или вследствие обмена веществом между системой и окружающей средой.

Уравнение (2.2) выражает взаимосвязь между общим свойством системы и свойствами каждого ее компонента. Приняв, что химический потенциал является постоянной величиной, проинтегрируем уравнение (2.2):

.

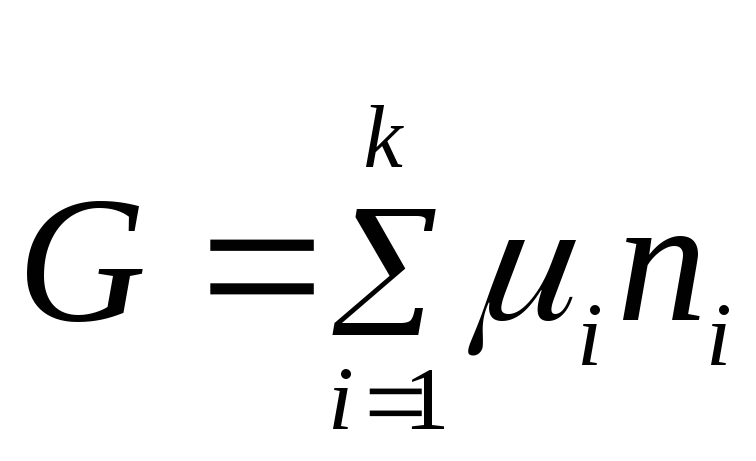Константа интегрирования равна нулю, поскольку, если все n i = 0, энергия Гиббса также равна нулю.

Для индивидуального вещества

,

т.е. химический потенциал индивидуального вещества равен мольной энергии Гиббса.

При равновесии dG = 0 и уравнение (2.1) принимает вид:

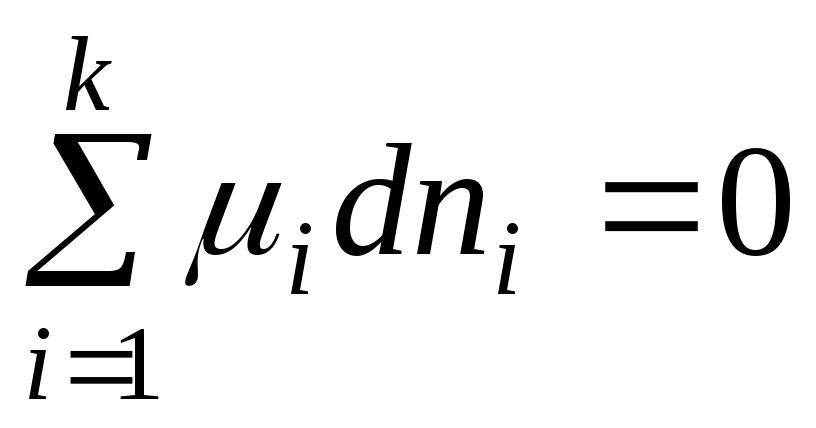. (2.3)

Полученное уравнение является общим условием равновесия в системе с переменным составом при р , Т = const .

Химический потенциал индивидуального идеального газа.

Рассмотрим термодинамическую систему, представляющую собой идеальный газ. Химический потенциал идеального газа равен:

,

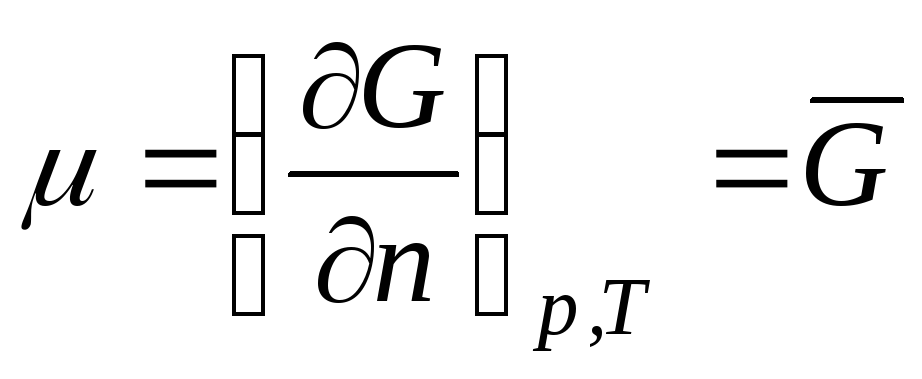где – мольная энергия Гиббса (изобарный потенциал 1 моль идеального газа).

,

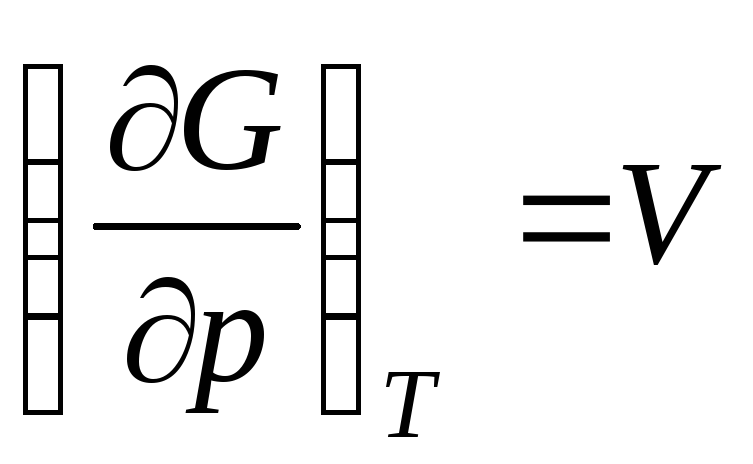то

,

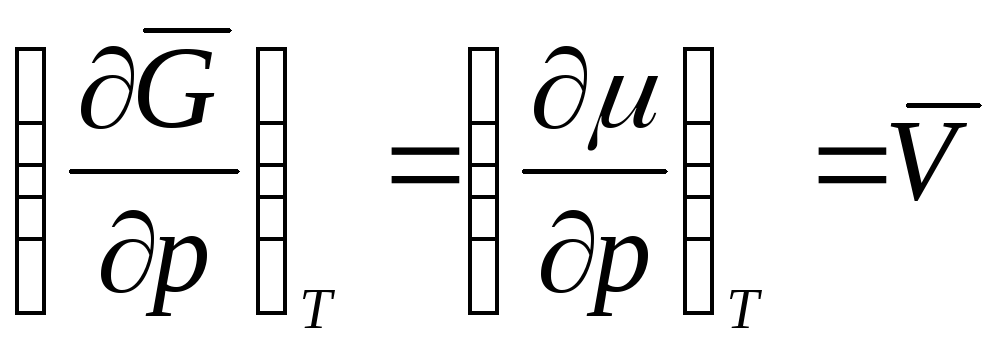где – мольный объем идеального газа (объем 1 моль газа).

Если процесс протекает при Т = const , частную производную можно заменить полной. Тогда

Уравнение состояния 1 моль идеального газа:

;

,

Проинтегрируем в интервале от р 0 до р :

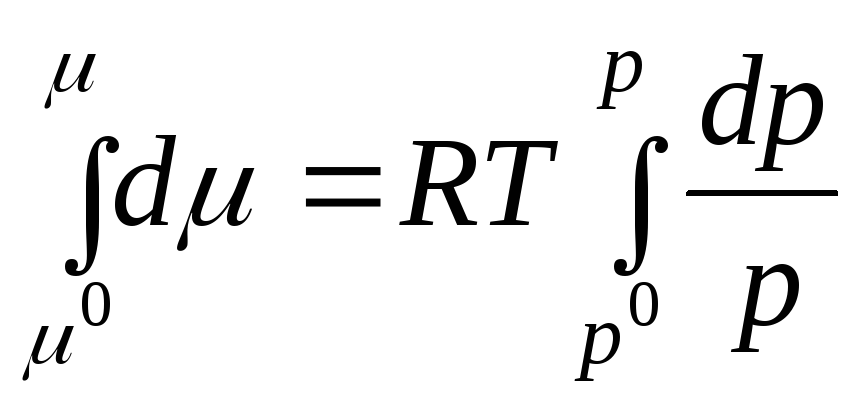
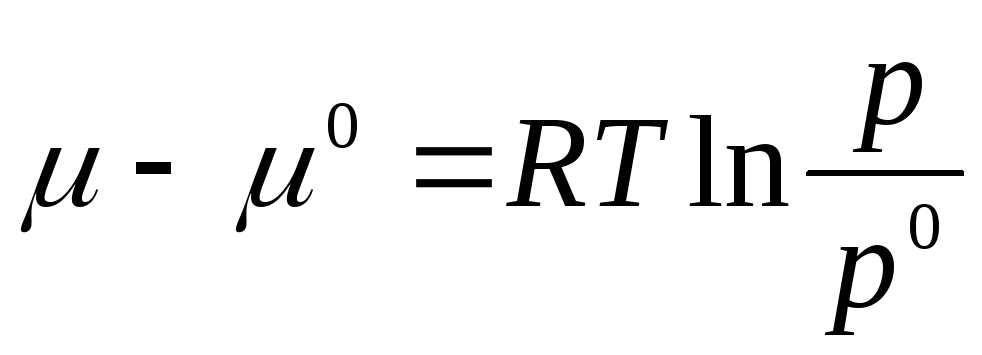
где μ 0 , р 0 – химический потенциал и давление идеального газа в стандартном состоянии.

За стандартное состояние принято состояние идеального газа при р 0 = 1 атм.

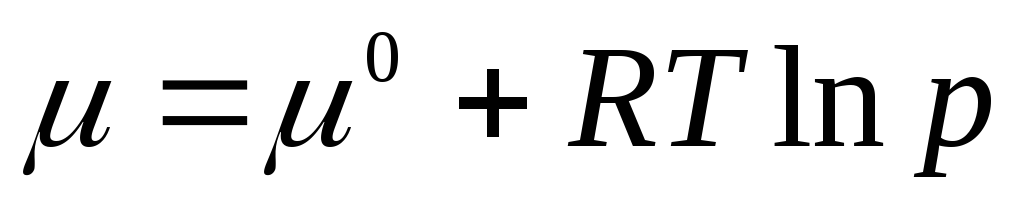. (2.3)

Стандартный химический потенциал – это химический потенциал при давлении газа 1 атм. Химический потенциал в стандартном состоянии μ 0 зависит только от температуры и не зависит от давления, т.е. μ 0 = f (T ). Из уравнения (2.3) видно, что под знаком логарифма стоит безразмерная величина, равная отношению давления р к стандартному давлению р 0 = 1 атм.

Поскольку μ = , можно записать

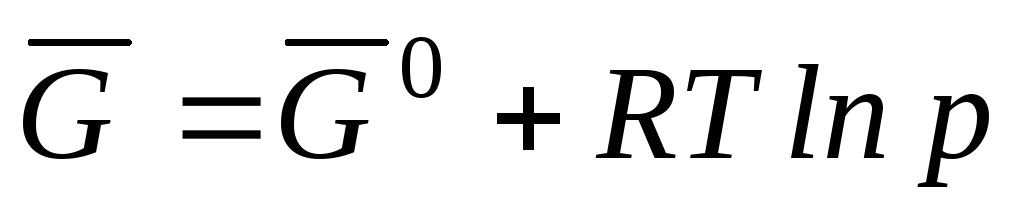
где

– стандартная мольная энергия Гиббса.

Химический потенциал компонента идеальных растворов.

Если общее давление газовой смеси невелико, то каждый газ будет оказывать свое собственное давление, причем такое, как если бы он один занимал весь объем. Это давление называется парциальным. Полное наблюдаемое давление р равно сумме парциальных давлений каждого газа (закон Дальтона):

.

Химический потенциал компонента смеси идеальных газов равен:

,

где р i – парциальное давление газа.

Выражая парциальное давление газа р i через общее давление и мольную долю газа x i , получают выражение для зависимости химического потенциала i -го компонента от мольной доли:

где – химический потенциал идеального газа приx i = 1 (т.е. в индивидуальном состоянии) при давлении р и температуре Т ; зависит и от температуры, и от давления.

Для идеальных жидких растворов применимо уравнение

,

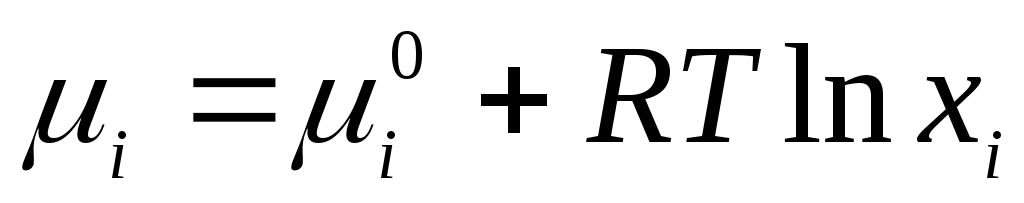где 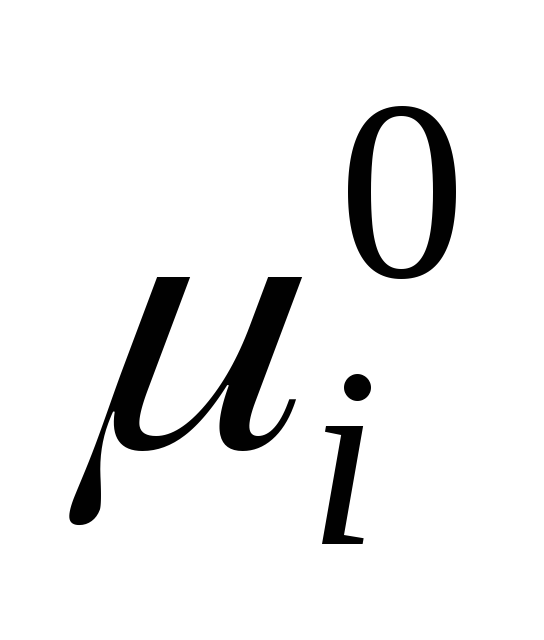– стандартный химический потенциал индивидуального компонента в жидком состоянии (

) зависит от температуры и давления;x i – мольная доля компонента.

Химический потенциал компонента реальных растворов .

Для реальных растворов все рассмотренные зависимости неприменимы. Химический потенциал компонента реального газового раствора рассчитывается по методу Льюиса. При этом для сохранения формы термодинамических уравнений вместо парциального давления в них вводят фиктивную величину f i , которая называется парциальной фугитивностью, или летучестью . Тогда

,

где – химический потенциал компонента реальной газовой смеси в стандартном состоянии.

Отношение летучести к парциальному давлению реального газового раствора называется коэффициентом летучести:

;

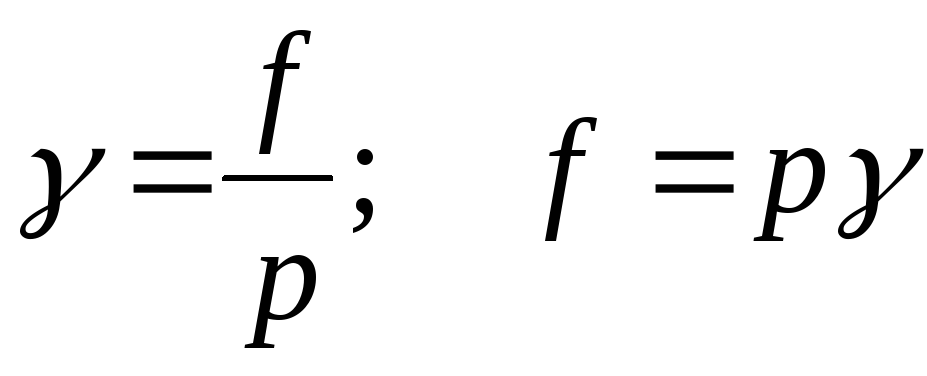Аналогично, для жидких реальных растворов действительную концентрацию заменяют соответствующей фиктивной величиной – активностью а i :

,

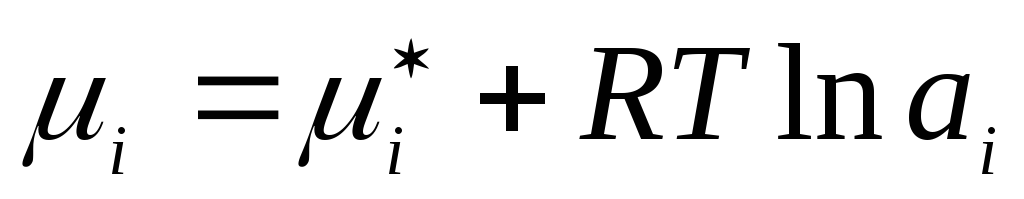где – химический потенциал компонента реального жидкого раствора в стандартном состоянии.

Активность связана с концентрацией через коэффициент активности:

,

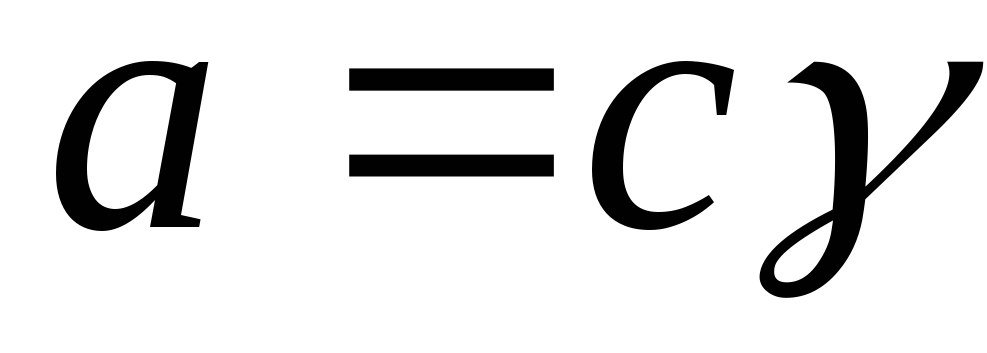где γ i – коэффициент активности.

В зависимости от способа выражения концентрации раствора различают рациональный, молярный и моляльный коэффициенты активности:

Коэффициент активности зависит от концентрации раствора. В бесконечно разбавленных растворах γ → 1, а i и f i → c i и p i соответственно.

Перепишем уравнение для химического потенциала в виде

,

следовательно, термодинамическая активность – это работа переноса 1 моль i -го компонента из стандартного раствора в данный реальный раствор.

Существует два основных способа выбора стандартного состояния – симметричный и несимметричный.

Симметричный способ. Выбирается одинаковое стандартное состояние для растворителя и растворенного вещества – состояние чистого компонента при температуре раствора. Тогда в стандартном состоянии x i = 1, a i = 1 и γ i = 1. Данный способ чаще применяется для растворов неэлектролитов.

Несимметричный способ. Выбирается различное стандартное состояние для растворителя и растворенного вещества. Для растворителя – как и в симметричном способе: x i → 1, a i → 1 и γ i → 1. Для растворенного вещества за стандартное состояние выбирается состояние вещества в бесконечно разбавленном растворе: x i → 0, a i → x i и γ i → 1. Способ наиболее часто используется в термодинамике растворов электролитов.