1. Să luăm un triunghi obișnuit.
2. Decupăm un triunghi din el, ale cărui vârfuri se află la mijlocul laturilor celui original. Ca rezultat, obținem trei triunghiuri pe plan, a căror aria fiecăruia este de patru ori mai mică decât aria celui original.
3. Efectuăm manipulările anterioare cu triunghiurile rezultate.

Procesul arată astfel:

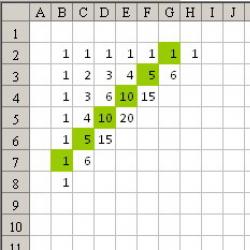
1. Interesant, dacă în triunghiul lui Pascal toate numerele impare sunt colorate într-o culoare și numerele pare alta, atunci se formează un triunghi Sierpinski.

Să profităm de acest fapt. Numai în Excel este mai convenabil să folosiți nu forma clasică (linie cu rând) a triunghiului lui Pascal, ci aceasta:

Aici coeficienții binomi se scriu în diagonală, în primul rând completat și prima coloană de unitate completată, iar în rest suma elementelor de sus și din stânga.

Să trecem la construcție. Pentru noi este suficient să notăm nu coeficienții, ci doar paritatea lor.

Mai întâi, să facem dimensiunea celulelor în Excel, de exemplu 7 pe 7 pixeli.

Să stăm în celula B2, apoi selectați zona B2:DY129 - pentru a face acest lucru, apăsați Ctrl + G și scrieți B2:DY129 în câmpul de legătură.

Acum, în bara de formule scriem =DACĂ(SAU(RÂND()=2, COLONA ()=2),1,REM(A2+B1,2))
și apăsați Ctrl + Enter pentru a umple întreaga zonă selectată cu o formulă similară.

Să mergem Meniul - Formatarea condițională iar pentru valoarea 1 indicăm culoarea celulei.

Ca rezultat obținem:

Trebuie remarcat faptul că triunghiul Sierpinski este obținut printr-un fel de mers aleatoriu în avion. Și anume:

1. Să fixăm 3 vârfuri ale triunghiului pe plan și să luăm un alt punct.
2. Obținem primul punct ca punct de mijloc al segmentului dintre accidental vârful și punctul selectat de la pasul 1.
3. Obținem al doilea punct ca punct de mijloc al segmentului dintre accidental vârful selectat și primul punct.
4. Repetăm ​​procesul de multe ori.

Puteți folosi această macrocomandă:

Sub macrocomandă publică()

Dim arRange(1 - 3) As Range
Dim tekRow ca întreg
Dim tekColumn ca întreg
Dim i ca întreg
Dim it As Integer

tekRow = Int(1000 * Rnd) + 1
tekColumn = Int(200 * Rnd) + 1

Set arRange(1) = Cells(1, 1)
Set arRange(2) = Cells(50, 250)
Set arRange(3) = Cells(200, 20)

Celulele.Clear

Pentru i = 1 până la 20000
iT = (Int(1000 * Rnd) Mod 3) + 1
tekRow = Int((tekRow + arRange(iT).Row) / 2)
tekColumn = Int((tekColumn + arRange(iT).Column) / 2)
Celule(tekRow, tekColumn).Interior.ColorIndex = 5
Următorul

End Sub

triunghiul Sierpinski- un fractal, unul dintre analogii bidimensionali ai mulțimii Cantor, propus de matematicianul polonez Waclaw Sierpinski în 1915. Cunoscut și sub numele de „Șervețelul” lui Sierpinski.

triunghiul Sierpinski

Constructie

Metoda iterativă

Construcția triunghiului Sierpinski

Punctele medii ale laturilor unui triunghi echilateral sunt conectate prin segmente. Primești 4 triunghiuri noi. Interiorul triunghiului din mijloc este îndepărtat din triunghiul original. Se dovedește mult T 1 (\displaystyle T_(1)), constând din cele 3 triunghiuri „primul rang” rămase. Făcând exact același lucru cu fiecare dintre triunghiurile de primul rang, obținem mulțimea T 2 (\displaystyle T_(2)), format din 9 triunghiuri echilaterale de rangul doi. Continuând acest proces la nesfârșit, obținem o succesiune infinită T 0 ⊃ T 1 ⊃ ⋯ ⊃ T n ⊃ … (\displaystyle T_(0)\supset T_(1)\supset \dots \supset T_(n)\supset \dots ), a cărui intersecție a membrilor este un triunghi Sierpinski.

Metoda haosului

1. Sunt specificate coordonatele atractorilor - vârfurile triunghiului original T 0 (\displaystyle T_(0)). 2. Spațiul probabilității (0 ; 1) (\displaystyle (0;1)) este împărțit în 3 părți egale, fiecare din care corespunde unui atractor. 3. Este specificat un anumit punct de plecare P 0 (\displaystyle P_(0)), situată în interiorul triunghiului T 0 (\displaystyle T_(0)). 4. Începutul ciclului de construire a punctelor aparținând mulțimii triunghiului Sierpinski. 1. Se generează un număr aleatoriu n ∈ (0 ; 1) (\displaystyle n\in (0;1)). 2. Atractorul activ devine vârful în al cărui subspațiu probabilistic a căzut numărul generat. 3. Se construiește un punct P i (\displaystyle P_(i)) cu coordonate noi: x i = x i − 1 + x A 2 ; y i = y i - 1 + y A 2 (\displaystyle x_(i)=(\frac (x_(i-1)+x_(A))(2));y_(i)=(\frac (y_(i)) -1)+y_(A))(2))), Unde: x i - 1 , y i - 1 (\displaystyle x_(i-1),y_(i-1))- coordonatele punctului anterior P i - 1 (\displaystyle P_(i-1)); x A , y A (\displaystyle x_(A),y_(A))- coordonatele punctului atractor activ. 5. Reveniți la începutul ciclului.

Proprietăți

Construire prin metoda iterativă

Construcție folosind metoda haosului

Note

Legături

Sistemul L

Sistemul L sau sistemul Lindenmayer este un sistem de rescriere paralelă și un tip de gramatică formală. Sistemul L constă dintr-un alfabet de simboluri care pot fi folosite pentru a crea șiruri, un set de reguli generatoare care specifică regulile de înlocuire pentru fiecare simbol, un șir inițial („axiomă”) de la care începe construcția și un mecanism pentru translatarea șirului generat în structuri geometrice. Sistemele L au fost propuse și dezvoltate în 1968 de Aristide Lindenmayer, un biolog și botanist maghiar la Universitatea din Utrecht. Lindenmayer a folosit sisteme L pentru a descrie comportamentul celulelor plantelor și a modela procesul de dezvoltare a plantelor. Sistemele L au fost, de asemenea, folosite pentru a modela morfologia diferitelor organisme și pot fi folosite pentru a genera fractali auto-similari, cum ar fi sistemele de funcții iterabile.

Rachetă (limbaj de programare)

Racket (fostă PLTScheme) este un limbaj de programare cu uz general multi-paradigmă aparținând familiei Lisp/Scheme. Oferă un mediu pentru programarea orientată pe limbaj - unul dintre scopurile racketului este crearea, dezvoltarea și implementarea limbajelor de programare. Limbajul este folosit în diverse contexte: ca limbaj de scripting, ca limbaj de uz general, în predarea informaticii, în cercetarea științifică.

Platforma oferă utilizatorului o implementare a limbajului Racket, inclusiv un sistem de rulare dezvoltat, diverse biblioteci, un compilator JIT etc., precum și mediul de dezvoltare DrRacket (cunoscut anterior ca DrScheme) scris în Racket. Acest cadru software este utilizat în cursul ProgramByDesign al MIT. Limbajul de bază Racket are un sistem macro puternic care vă permite să creați limbaje de programare încorporate și specifice domeniului, construcții de limbaj (de exemplu, clase și module) și dialecte Racket cu semantică diferită.

Sistemul este un software gratuit și open source distribuit în condiții LGPL. Extensiile și pachetele scrise de comunitate sunt disponibile pe PLAneT, distribuția web a sistemului.

Algoritm de compresie fractală

Compresia imaginii fractale este un algoritm de compresie a imaginii cu pierderi bazat pe aplicarea unor sisteme de funcții iterate (de obicei transformări afine) la imagini. Acest algoritm este cunoscut pentru faptul că în unele cazuri permite obținerea unor rapoarte de compresie foarte mari cu o calitate vizuală acceptabilă pentru fotografii reale ale obiectelor naturale. Din cauza situației dificile cu brevetarea, algoritmul nu a fost utilizat pe scară largă.

Tigla despărțitoare

Rep-tila este un concept de geometrie mozaic, o figură care poate fi tăiată în copii mai mici ale figurii în sine. În 2012, matematicianul englez Lee Salous a propus în Mathematics Magazine o generalizare a plăcilor de împărțire numită set de plăci auto-tiling.

Regula finală de împărțire

În matematică, regula supremă a subdiviziunii este un mod recursiv de a împărți un poligon și alte forme bidimensionale în bucăți din ce în ce mai mici. Regulile de subdiviziune în acest sens sunt o generalizare a fractalilor. În loc să repeți același model iar și iar, există schimbări subtile la fiecare pas, permițând structuri mai bogate, păstrând în același timp stilul fractal elegant. Regulile de subdiviziune sunt folosite în arhitectură, biologie și informatică, precum și în studiul varietăților hiperbolice. Înlocuirea plăcilor este un tip de regulă de subdiviziune bine studiat.

curba Peano

Curba Peano este un nume general pentru curbele parametrice a căror imagine conține un pătrat (sau, mai general, regiuni deschise ale spațiului). Un alt nume este o curbă de umplere a spațiului.

Numită după Giuseppe Peano (1858-1932), descoperitorul acestui tip de curbă, curba Peano este numele dat curbei specifice pe care a găsit-o Peano.

curba Sierpinski

curbe Sierpinski este o secvență definită recursiv de curbe fractale plane închise continue descoperite de Waclaw Sierpinski. Curba din limită la umple complet pătratul unității, deci curba limită, numită și curba Sierpinski, este un exemplu de curbe de umplere a spațiului.

Deoarece curba Sierpinski umple spațiul, dimensiunea sa Hausdorff (în limita la n → ∞ (\displaystyle n\rightarrow \infty )) este egal cu 2 (\displaystyle 2).
Lungimea curbei euclidiene

egal cu l n = 2 3 (1 + 2) 2 n − 1 3 (2 − 2) 1 2 n (\displaystyle l_(n)=(2 \over 3)(1+(\sqrt (2)))2^( n)-(1 \peste 3)(2-(\sqrt (2)))(1 \peste 2^(n))),

adică este în creștere exponenţial De n (\displaystyle n), iar limita la n → ∞ (\displaystyle n\rightarrow \infty ) zona regiunii delimitată de curbă S n (\displaystyle S_(n)), este 5/12 (\displaystyle 5/12) pătrat (în metrica euclidiană).

Logaritm

Logaritmul unui număr b (\displaystyle b) bazat pe a (\displaystyle a) (din greaca veche. λόγος "cuvânt; atitudine" + ἀριθμός „număr”) este definit ca un indicator al puterii la care trebuie ridicată baza a (\displaystyle a) pentru a obține numărul b (\displaystyle b). Desemnare: log a ⁡ b (\displaystyle \log _(a)b), pronunțat: „ logaritm b (\displaystyle b) bazat pe a (\displaystyle a) ».

Din definiție rezultă acea constatare x = log a ⁡ b (\displaystyle x=\log _(a)b) este echivalent cu rezolvarea ecuației a x = b (\displaystyle a^(x)=b). De exemplu, log 2 ⁡ 8 = 3 (\displaystyle \log _(2)8=3), deoarece 2 3 = 8 (\displaystyle 2^(3)=8).

Calcularea logaritmului se numește prin logaritm. Numerele a , b (\displaystyle a,b) cel mai adesea reale, dar există și o teorie a logaritmilor complecși.

Logaritmii au proprietăți unice care au determinat utilizarea lor pe scară largă pentru a simplifica semnificativ calculele care necesită forță de muncă. Când treceți „în lumea logaritmilor”, înmulțirea este înlocuită cu o adunare mult mai simplă, împărțirea este înlocuită cu scădere, iar exponențiația și extragerea rădăcinii sunt transformate, respectiv, în înmulțire și împărțire cu exponent. Laplace a spus că inventarea logaritmilor, „prin scurtarea muncii astronomului, i-a dublat viața”.

Definiția logaritmilor și un tabel al valorilor acestora (pentru funcțiile trigonometrice) au fost publicate pentru prima dată în 1614 de către matematicianul scoțian John Napier. Tabelele logaritmice, extinse și rafinate de alți matematicieni, au fost utilizate pe scară largă pentru calcule științifice și de inginerie timp de mai bine de trei secole, până la apariția calculatoarelor electronice și a calculatoarelor.

De-a lungul timpului, a devenit clar că funcția logaritmică y = log a ⁡ x (\displaystyle y=\log _(a)x) este de neînlocuit în multe alte domenii ale activității umane: rezolvarea ecuațiilor diferențiale, clasificarea valorilor cantităților (de exemplu, frecvența și intensitatea sunetului), aproximarea diferitelor dependențe, teoria informațiilor, teoria probabilității etc. Această funcție este una dintre cele elementare, este inversul funcţiei exponenţiale. Cei mai des utilizați sunt logaritmii reali cu baze 2 (\displaystyle 2)(binar), e (\displaystyle e) (logaritm natural) și 10 (\displaystyle 10)(zecimal).

Nanotehnologie bazată pe ADN

Nanotehnologia ADN este dezvoltarea și producerea de structuri artificiale din acizi nucleici pentru uz tehnologic. În acest domeniu științific, acizii nucleici sunt folosiți nu ca purtători de informații genetice în celulele vii, ci ca material pentru nevoile de inginerie non-biologică a nanomaterialelor.

Tehnologia folosește reguli stricte pentru împerecherea de baze a acizilor nucleici, care permit numai unor părți ale catenelor cu secvențe de baze complementare să fie legate între ele pentru a forma o structură puternică și rigidă cu dublu helix. Din aceste reguli, devine posibil să se construiască secvențe de baze care vor fi asamblate selectiv pentru a forma structuri țintă complexe cu forme și proprietăți la scară nanometrică reglate precis. Majoritatea materialelor sunt realizate folosind ADN, dar au fost construite și structuri care încorporează alți acizi nucleici precum ARN și acizi nucleici peptidici (PNA), permițând ca domeniul tehnologic să fie numit „nanotehnologie pe bază de nucleotide”.

Conceptul de bază al nanotehnologiei bazate pe ADN a fost propus pentru prima dată la începutul anilor 1980 de către Nadrian Seaman, iar acest domeniu de cercetare a început să atragă un interes larg la mijlocul anilor 2000. Cercetătorii care lucrează în acest domeniu emergent al tehnologiei au creat structuri statice, cum ar fi rețele cristaline bi- și tridimensionale, nanotuburi, poliedre și alte forme libere, precum și structuri funcționale precum mașini moleculare și calculatoare ADN.

Pentru a asambla aceste structuri sunt utilizate o varietate de tehnici, inclusiv structurarea plăcilor, în care plăcile sunt asamblate din structuri mai mici, structuri pliabile create folosind tehnica origami ADN și structuri rearanjate dinamic create folosind tehnici de deplasare a firelor. Domeniul de cercetare începe să fie folosit ca instrument de rezolvare a problemelor științifice de bază în domeniile biologiei structurale și biofizicii, inclusiv probleme aplicate de cristalografie și spectroscopie pentru determinarea structurii proteinelor. De asemenea, sunt în curs de desfășurare cercetări pentru potențiale aplicații în electronica moleculară scalabilă și nanomedicină.

Logaritmul natural

Logaritmul natural este logaritmul la bază e, Unde e (\displaystyle e)- o constantă irațională egală cu aproximativ 2,72. Se notează ca ln ⁡ x (\displaystyle \ln x), log e ⁡ x (\displaystyle \log _(e)x) sau uneori doar log ⁡ x (\displaystyle \log x), dacă baza e (\displaystyle e) subînțeles. De obicei numărul x (\displaystyle x) sub semnul logaritmului este real, dar acest concept poate fi extins la numere complexe.

Din definiție rezultă că dependența logaritmică este funcția inversă pentru exponențial y = e x (\displaystyle y=e^(x)), prin urmare graficele lor sunt simetrice față de bisectoarea primului și al treilea cadran (vezi figura din dreapta). Ca și funcția exponențială, și funcția logaritmică aparține categoriei funcțiilor transcendentale.

Logaritmii naturali sunt utili pentru rezolvarea ecuațiilor algebrice în care necunoscutul este prezent ca exponent și sunt indispensabili în analiza matematică. De exemplu, logaritmii sunt utilizați pentru a găsi constanta de dezintegrare pentru un timp de înjumătățire cunoscut sau pentru a găsi timpul de dezintegrare în rezolvarea problemelor de radioactivitate. Ele joacă un rol important în multe domenii ale matematicii și științelor aplicate și sunt utilizate în finanțe pentru a rezolva multe probleme, inclusiv găsirea interesului compus.

Dimensiunea Lebesgue

Dimensiunea Lebesgue sau dimensiune topologică- dimensiune definită de acoperiri, cel mai important invariant al spațiului topologic. Dimensiunea Lebesgue a spațiului X (\displaystyle X) de obicei notate dim ⁡ X (\displaystyle \dim X).

Recursiune

Recursiunea este o definiție, descriere, imagine a unui obiect sau proces în cadrul acestui obiect sau proces însuși, adică o situație în care un obiect face parte din el însuși. Termenul „recursiune” este folosit în diverse domenii de specialitate ale cunoașterii - de la lingvistică la logică, dar este folosit cel mai pe scară largă în matematică și informatică.

Sierpinski, Waclaw

Wacław Franciszek Sierpiński, într-o altă transcriere - Sierpiński (poloneză: Wacław Franciszek Sierpiński; 14 martie 1882, Varșovia - 21 octombrie 1969, ibid.) - matematician și profesor polonez, cunoscut pentru lucrările sale despre teoria mulțimilor, axioma alegerii, ipoteza continuumului, teoria numerelor, teoria funcțiilor și topologia. Autor a 724 de articole și 50 de cărți.

Tetraedru (Bottrop)

Tetraedrul (germană: Tetraeder) este o structură de oțel sub formă de tetraedru cu lungimea marginii de 60 m, susținută de patru suporturi de beton de 9 metri, folosită ca punte de observație, în orașul Bottrop (Renania de Nord-Westfalia) . Tetraedrul este situat deasupra mormanei de deșeuri Beckstraße (germană: Beckstraße) a minei Prosper-Haniel (de: Bergwerk Prosper-Haniel) la o altitudine de 105 m deasupra nivelului mării. De pe puntea de observație de sus puteți vedea vederi ale orașelor Bottrop, Essen, Oberhausen, Gladbeck. Cu o vizibilitate bună, raza de vizionare ajunge la 40 km și vă permite chiar să distingeți turnul de televiziune Rheinturm din Düsseldorf.

Tetraedrul Bottrop este punctul tematic al proiectului regional „Calea culturii industriale” din regiunea Ruhr.

triunghiul lui Pascal

Triunghiul lui Pascal este un tabel infinit de coeficienți binomi având formă triunghiulară. În acest triunghi, există unele în partea de sus și pe laterale. Fiecare număr este egal cu suma celor două numere de deasupra lui. Liniile triunghiului sunt simetrice față de axa verticală. Numit după Blaise Pascal. Numerele care alcătuiesc triunghiul lui Pascal apar în mod natural în algebră, combinatorică, teoria probabilităților, analiza matematică și teoria numerelor.

Fractal

Fractal (lat. fractus - zdrobit, spart, spart) este o mulțime care are proprietatea auto-asemănării (un obiect care coincide exact sau aproximativ cu o parte din sine, adică întregul are aceeași formă cu unul sau mai multe părți). În matematică, fractalii sunt înțeleși ca mulțimi de puncte din spațiul euclidian care au o dimensiune metrică fracțională (în sensul lui Minkowski sau Hausdorff), sau o dimensiune metrică diferită de cea topologică, deci ar trebui să se distingă de alte figuri geometrice limitate de un număr finit de legături. Figurile auto-asemănătoare care se repetă de un număr finit de ori se numesc prefractali.

Primele exemple de mulțimi autosimilare cu proprietăți neobișnuite au apărut în secolul al XIX-lea ca urmare a studiului funcțiilor continue nediferențiabile (de exemplu, funcția Bolzano, funcția Weierstrass, mulțimea Cantor). Termenul „fractal” a fost introdus de Benoit Mandelbrot în 1975 și a devenit cunoscut pe scară largă odată cu publicarea cărții sale „Fractal Geometry of Nature” în 1977. Fractalii au câștigat o popularitate deosebită odată cu dezvoltarea tehnologiilor informatice, ceea ce a făcut posibilă vizualizarea eficientă a acestor structuri.

Cuvântul „fractal” este folosit nu numai ca termen matematic. Un fractal poate fi numit un obiect care are cel puțin una dintre următoarele proprietăți:

Are o structură non-trivială la toate scările. Acest lucru este în contrast cu figurile obișnuite (cum ar fi un cerc, o elipsă, un grafic al unei funcții netede): dacă luați în considerare un mic fragment dintr-o figură obișnuită la o scară foarte mare, acesta va arăta ca un fragment de linie dreaptă. Pentru un fractal, creșterea scării nu duce la o simplificare a structurii, adică la toate scările puteți vedea o imagine la fel de complexă.

Este auto-similar sau aproximativ auto-similar.

Are o dimensiune metrică fracționată sau o dimensiune metrică care o depășește pe cea topologică Multe obiecte din natură au proprietăți fractale, de exemplu: coaste, nori, coroane de copaci, fulgi de nea, sistemul circulator, alveole.

Dimensiune fractală

Dimensiune fractală(Dimensiunea fractală engleză) - una dintre modalitățile de a determina dimensiunea unui set în spațiu metric. Dimensiune fractală n-multimea dimensionala poate fi definita folosind formula:

D = − lim ε → 0 ln ⁡ (N ε) ln ⁡ (ε) (\displaystyle D=-\lim \limits _(\varepsilon \to 0)(\frac (\ln(N_(\varepsilon ))) (\ln(\varepsilon)))), Unde N ε (\displaystyle N_(\varepsilon ))- număr minim n- „bile” dimensionale de rază ε (\displaystyle \varepsilon), necesar pentru acoperirea setului.

Dimensiunea fractală poate lua o valoare numerică non-întreg.

Ideea de bază a dimensiunii fracturate are o istorie lungă în domeniul matematicii, dar termenul în sine a fost inventat de Benoit Mandelbrot în 1967 în articolul său despre auto-asemănarea, în care a descris dimensiunea fracțională. În acest articol, Mandelbrot s-a referit la lucrările anterioare ale lui Lewis Fry Richardson, care descriu ideea contraintuitivă că lungimea măsurată a unei linii de țărm depinde de lungimea unui baston de măsurare (vezi Figura 1). Urmând această idee, dimensiunea fractală a unei linii de coastă corespunde raportului dintre numărul de poli (la o anumită scară) necesar pentru a măsura lungimea liniei de coastă la scara aleasă a polului. Există mai multe definiții matematice formale [⇨] ale dimensiunii fractale care se bazează pe acest concept de bază al schimbării unui element cu o schimbare de scară.

Un exemplu elementar este dimensiunea fractală a fulgului de zăpadă Koch. Dimensiunea sa topologică este 1, dar nu este nicidecum o curbă rectificabilă, deoarece lungimea curbei dintre oricare două puncte ale unui fulg de zăpadă Koch este infinită. Nicio parte a unei curbe, oricât de mică, nu este un segment de linie dreaptă. Mai degrabă, fulgul de zăpadă al lui Koch constă dintr-un număr infinit de segmente conectate în unghiuri diferite. Dimensiunea fractală a unei curbe poate fi explicată intuitiv sugerând că o linie fractală este un obiect prea detaliat (detaliat) pentru a fi unidimensional, dar nu suficient de complex pentru a fi bidimensional. Prin urmare, dimensiunea sa este mai bine descrisă nu prin dimensiunea topologică obișnuită 1, ci prin dimensiunea sa fractală, egală în acest caz cu un număr situat în intervalul dintre 1 și 2.

Artă fractală

Arta fractală este o formă de artă algoritmică creată prin calculul obiectelor fractale și prin prezentarea rezultatelor calculelor ca imagini statice, animații și fișiere media generate automat. Arta fractală a început la mijlocul anilor 1980. Este un gen de artă computerizată și artă digitală care face parte din arta new media. În același timp, arta fractală este una dintre domeniile așa-numitei „arte științifice”.

Arta fractală este rareori creată manual. Este de obicei creat indirect de software care generează fractali prin trei pași: setarea parametrilor software-ului fractal corespunzător; efectuarea de calcule eventual lungi; și evaluări ale produselor. În unele cazuri, alte programe grafice sunt folosite pentru a procesa în continuare imaginile generate. Imaginile non-fractale pot fi incluse și într-o operă de artă. Setul Julia și Setul Mandelbrot sunt considerate icoane ale artei fractale.

Caracteristici
Cei mai simpli fractali

Pentru a-l obține, trebuie să luați un triunghi (echilateral) cu interior, să desenați linii de mijloc în el și să aruncați pe cel central dintre cele patru triunghiuri mici formate. Apoi trebuie să repetați aceiași pași cu fiecare dintre cele trei triunghiuri rămase etc. Imaginea arată primii trei pași, iar în demonstrația flash puteți exersa și obține pași până la al zecelea.

Aruncarea triunghiurilor centrale nu este singura modalitate de a ajunge la un triunghi Sierpinski. Vă puteți deplasa „în direcția opusă”: luați un triunghi inițial „gol”, apoi completați triunghiul format din liniile de mijloc din el, apoi faceți același lucru în fiecare dintre cele trei triunghiuri de colț etc. La început, figurile vor fie foarte diferite, dar cu Pe măsură ce numărul de iterații crește, acestea vor deveni din ce în ce mai asemănătoare între ele, iar în limită vor coincide.

Următorul mod de a obține un triunghi Sierpinski este și mai asemănător cu schema obișnuită de construire a fractalilor geometrici prin înlocuirea părților următoarei iterații cu un fragment la scară. Aici, la fiecare pas, segmentele care alcătuiesc linia întreruptă sunt înlocuite cu o linie întreruptă de trei legături (ea însăși se obține în prima iterație). Trebuie să așezați această linie întreruptă alternativ la dreapta și apoi la stânga. Se poate observa că deja a opta iterație este foarte aproape de fractal și, cu cât merge mai departe, cu atât linia se va apropia de el.

Dar asta nu este tot. Se dovedește că triunghiul Sierpinski este obținut ca urmare a uneia dintre varietățile de mers aleatoriu a unui punct pe un plan. Această metodă se numește „jocul haos”. Cu ajutorul lui, puteți construi și alți fractali.

Esența „jocului” este aceasta. Un triunghi regulat este fixat pe un plan A 1 A 2 A 3. Marcați orice punct de plecare B 0 . Apoi selectați aleatoriu unul dintre cele trei vârfuri ale triunghiului și marcați punctul B 1 - mijlocul unui segment cu capete la acest vârf și la B 0 (în figura din dreapta, vârful a fost selectat aleatoriu A 1). Același lucru se repetă cu un punct B 1 pentru a obține B 2. Apoi primesc punctele B 3 , B 4 etc. Important este ca punctul să „sare” aleatoriu, adică de fiecare dată când vârful triunghiului este ales aleatoriu, indiferent de ceea ce s-a ales în pașii anteriori. Este uimitor că dacă marchezi puncte dintr-o secvență B i, atunci triunghiul Sierpinski va începe în curând să apară. Mai jos este ce se întâmplă când sunt marcate 100, 500 și 2500 de puncte.

Unele proprietăți

Opțiuni

Covor (pătrat, șervețel) de Sierpinski. Versiunea pătrată a fost descrisă de Wacław Sierpinski în 1916. El a reușit să demonstreze că orice curbă care poate fi trasată pe un plan fără auto-intersecții este homeomorfă pentru un subset al acestui pătrat cu gauri. Ca un triunghi, un pătrat poate fi făcut din diferite modele. În dreapta este metoda clasică: împărțirea pătratului în 9 părți și aruncarea părții centrale. Apoi se repetă același lucru pentru restul de 8 pătrate etc.

Asemenea unui triunghi, un pătrat are zonă zero. Dimensiunea fractală a unui covor Sierpinski este egală cu log 3 8, calculată în mod similar cu dimensiunea unui triunghi.

Piramida Sierpinski. Unul dintre analogii tridimensionali ai triunghiului Sierpinski. Este construit într-un mod similar, ținând cont de tridimensionalitatea a ceea ce se întâmplă: 5 copii ale piramidei inițiale, comprimate de două ori, alcătuiesc prima iterație, cele 5 copii ale sale vor alcătui a doua iterație etc. Fractalul dimensiunea este egală cu log 2 5. Figura are volum zero (la fiecare pas se aruncă jumătate din volum), dar în același timp aria suprafeței este păstrată de la iterație la iterație, iar pentru fractal este aceeași ca și pentru piramida initiala.

buretele lui Menger. Generalizarea covorului Sierpinski în spațiu tridimensional. Pentru a construi un burete, aveți nevoie de o repetiție nesfârșită a procedurii: fiecare dintre cuburile care alcătuiesc iterația este împărțit în 27 de cuburi de trei ori mai mici, din care cel central și cei 6 vecini ai săi sunt aruncați afară. Adică, fiecare cub generează 20 de noi, de trei ori mai mici. Prin urmare, dimensiunea fractalului este log 3 20. Acest fractal este o curbă universală: orice curbă din spațiul tridimensional este homeomorfă pentru un anumit subset al buretelui. Buretele are volum zero (deoarece la fiecare pas se inmulteste cu 20/27), dar are o suprafata infinit de mare.

L
linia Oman:

N – numărul de segmente, dimensiune A.

D – „gradul de îndoire”

N=(1/a)D; S=N*a; S=(1/a)D-1

LA
Riva Koch

2) N=4L=1/3S(4)=4/3

N=16 L=1/9S(16)=16/9

Dimensiune fractală:

D=lg4 /lg3=1,26...

Dimensiunea fractală a unui set

Volumul fractalului din sa încorporarea spațiului este întotdeauna zero. Totuși, poate fi diferit de zero într-un spațiu de dimensiune inferioară. Pentru a determina dimensiunea acestui spațiu D, hai să spargem totul n-spațiu dimensional în cuburi mici cu lungimea muchiei ε și volum ε n- Fig. 1. Lăsa N(ε ) este numărul minim de cuburi care împreună acoperă complet mulțimea fractală, apoi prin definiție

Existența acestei limite înseamnă că volumul fractal este finit D-spaţiu dimensional: cu mic ε

şi spre deosebire de dimensiunea obişnuită D poate fi o valoare fracțională, ceea ce este cel mai adesea pentru seturile fractale.

Evident, pentru seturile obișnuite această definiție duce la rezultate binecunoscute. Deci pentru mulțime N puncte izolate pe care le avem N(ε ) =N prin urmare

Pentru un segment, o linie netedă de lungime este suficientă L:N(ε ) =L/ε prin urmare D= 1. Pentru site S suprafata bidimensionala: N(ε ) =S/ε 2 și D= 2 etc.

Algoritm recursiv pentru construirea de fractali constructivi.

1. triunghiul Sierpinski

triunghiul Sierpinski

triunghiul Sierpinski- un fractal, unul dintre analogii bidimensionali ai setului Cantor propus de matematicianul polonez Sierpinski în 1915. Cunoscut și sub numele de „grilă” sau „șervețel” Sierpinski.

Constructie

Se ia un triunghi echilateral solid, iar în primul pas interiorul triunghiului din mijloc este îndepărtat din centru. La a doua etapă, cele trei triunghiuri din mijloc sunt îndepărtate din cele trei triunghiuri rămase etc. După repetarea nesfârșită a acestei proceduri, rămâne o submulțime a triunghiului solid - triunghiul Sierpinski.

Construcția triunghiului Sierpinski

Triunghiul Sierpinski poate fi obținut și folosind următorul algoritm:

Luați trei puncte pe plan și desenați un triunghi.

Selectați aleatoriu orice punct din interiorul triunghiului și mutați jumătate din distanța de la acest punct la oricare dintre cele trei vârfuri ale triunghiului.

Marcați poziția curentă.

Repetați de la pasul 2.

Conceptele de geometrie fractală și fractală, care au apărut la sfârșitul anilor '70, au devenit ferm stabilite în rândul matematicienilor și programatorilor încă de la mijlocul anilor '80. Cuvântul fractal este derivat din latinescul fractus și înseamnă format din fragmente. A fost propus de Benoit Mandelbrot în 1975 pentru a se referi la structurile neregulate, dar auto-asemănătoare de care era preocupat. Nașterea geometriei fractale este de obicei asociată cu publicarea cărții lui Mandelbrot „The Fractal Geometry of Nature” în 1977. Lucrările sale au folosit rezultatele științifice ale altor oameni de știință care au lucrat în perioada 1875-1925 în același domeniu (Poincaré, Fatou, Julia, Cantor, Hausdorff Dar numai în vremea noastră a fost posibilă combinarea muncii lor într-un singur sistem.
Rolul fractalilor în grafica computerizată astăzi este destul de mare. Aceștia vin în ajutor, de exemplu, atunci când este necesar, folosind mai mulți coeficienți, să definească linii și suprafețe de forme foarte complexe. Din punctul de vedere al graficii pe computer, geometria fractală este indispensabilă atunci când se generează nori artificiali, munți și suprafețe maritime. De fapt, s-a găsit o modalitate de a reprezenta cu ușurință obiecte complexe non-euclidiene, ale căror imagini sunt foarte asemănătoare cu cele naturale.
Una dintre principalele proprietăți ale fractalilor este auto-asemănarea. În cel mai simplu caz, o mică parte a unui fractal conține informații despre întregul fractal. Definiția lui Mandelbrot a unui fractal este: „Un fractal este o structură formată din părți care sunt într-un anumit sens similare cu întregul”.

Există un număr mare de obiecte matematice numite fractali (triunghiul Sierpinski, fulg de zăpadă Koch, curba Peano, set Mandelbrot și atractori Lorentz). Fractalii descriu cu mare acuratețe multe fenomene fizice și formațiuni ale lumii reale: munți, nori, curgeri turbulente (vortex), rădăcini, ramuri și frunze de copaci, vase de sânge, ceea ce este departe de a corespunde unor simple figuri geometrice. Pentru prima dată, Benoit Mandelbrot a vorbit despre natura fractală a lumii noastre în lucrarea sa fundamentală „Geometria fractală a naturii”.
Termenul fractal a fost introdus de Benoit Mandelbrot în 1977 în lucrarea sa fundamentală Fractals, Form, Chaos and Dimension. Potrivit lui Mandelbrot, cuvântul fractal provine din cuvintele latine fractus - fracțional și frangere - a rupe, care reflectă esența unui fractal ca un set „rupt”, neregulat.

Clasificarea fractalilor.

Pentru asta Pentru a prezenta întreaga varietate de fractali, este convenabil să se recurgă la clasificarea lor general acceptată. Există trei clase de fractali.

1. Fractali geometrici.

Fractalii din această clasă sunt cei mai vizuali. În cazul bidimensional, acestea sunt obținute folosind o linie întreruptă (sau suprafață în cazul tridimensional), numită generator. Într-un pas al algoritmului, fiecare dintre segmentele care alcătuiesc linia întreruptă este înlocuit cu polilinie-generator la o scară adecvată. Ca urmare a repetării nesfârșite a acestei proceduri, se obține un fractal geometric.

Să ne uităm la un exemplu al unuia dintre aceste obiecte fractale - curba Koch triadică.

Construcția curbei Koch triadice.

Să luăm un segment drept de lungime 1. Să-i spunem sămânță. Să împărțim sămânța în trei părți egale de 1/3 lungime, să aruncăm partea de mijloc și să o înlocuim cu o linie întreruptă de două verigi de 1/3 lungime.

Vom obține o linie întreruptă formată din 4 legături cu o lungime totală de 4/3, așa că sunăm prima generatie.

Pentru a trece la următoarea generație a curbei Koch, este necesar să aruncați și să înlocuiți partea de mijloc a fiecărei legături. În consecință, lungimea celei de-a doua generații va fi de 16/9, a treia – 64/27. dacă continuăm acest proces la infinit, rezultatul este o curbă Koch triadică.

Să luăm acum în considerare proprietățile curbei Koch triadice și să aflăm de ce fractalii au fost numiți „monstri”.

În primul rând, această curbă nu are lungime - după cum am văzut, cu numărul de generații lungimea ei tinde spre infinit.

În al doilea rând, este imposibil să construiți o tangentă la această curbă - fiecare dintre punctele sale este un punct de inflexiune în care derivata nu există - această curbă nu este netedă.

Lungimea și netezimea sunt proprietățile fundamentale ale curbelor, care sunt studiate atât de geometria euclidiană, cât și de geometria lui Lobachevsky și Riemann. Metodele tradiționale de analiză geometrică s-au dovedit a fi inaplicabile curbei Koch triadice, astfel încât curba Koch s-a dovedit a fi un monstru - un „monstru” printre locuitorii netezi ai geometriilor tradiționale.

Construcția „balaurului” Harter-Haithway.

Pentru a obține un alt obiect fractal, trebuie să schimbați regulile de construcție. Fie ca elementul de formare să fie două segmente egale conectate în unghi drept. În generația zero înlocuiți segmentul unitar cu acest element de formare astfel încât colțul să fie deasupra. Putem spune că cu o astfel de înlocuire are loc o deplasare a mijlocului legăturii. La construirea generațiilor ulterioare, se respectă regula: prima verigă din stânga este înlocuită cu un element de formare, astfel încât mijlocul legăturii să fie deplasat la stânga direcției de mișcare, iar la înlocuirea legăturilor ulterioare, direcțiile de deplasarea mijlocului segmentelor trebuie alternată. Figura prezintă primele câteva generații și a 11-a generație a curbei construite conform principiului descris mai sus. O curbă cu n care tinde spre infinit se numește dragonul Harter-Haithway.
În grafica computerizată, utilizarea fractalilor geometrici este necesară atunci când se obține imagini cu copaci și tufișuri. Fractalii geometrici bidimensionali sunt folosiți pentru a crea texturi tridimensionale (modele pe suprafața unui obiect).

2.Fractali algebrici

Acesta este cel mai mare grup de fractali. Ele sunt obținute folosind procese neliniare în spații n-dimensionale. Procesele bidimensionale sunt cele mai studiate. Atunci când interpretăm un proces iterativ neliniar ca un sistem dinamic discret, se poate folosi terminologia teoriei acestor sisteme: portret de fază, proces în stare staționară, atractor etc.
Se știe că sistemele dinamice neliniare au mai multe stări stabile. Starea în care se află sistemul dinamic după un anumit număr de iterații depinde de starea sa inițială. Prin urmare, fiecare stare stabilă (sau, după cum se spune, atractor) are o anumită regiune de stări inițiale, din care sistemul va cădea în mod necesar în stările finale luate în considerare. Astfel, spațiul de fază al sistemului este împărțit în zone de atracție a atractorilor. Dacă spațiul de fază este un spațiu bidimensional, atunci prin colorarea zonelor de atracție cu culori diferite se poate obține un portret de fază color al acestui sistem (proces iterativ). Schimbând algoritmul de selecție a culorii, puteți obține modele fractale complexe cu modele multicolore bizare. O surpriză pentru matematicieni a fost capacitatea de a genera structuri non-triviale foarte complexe folosind algoritmi primitivi.

Set Mandelbrot.

Ca exemplu, luați în considerare mulțimea Mandelbrot. Algoritmul pentru construcția sa este destul de simplu și se bazează pe o expresie iterativă simplă: Z = Z * Z + C, Unde ZiȘi C- variabile complexe. Iterațiile sunt efectuate pentru fiecare punct de plecare dintr-o regiune dreptunghiulară sau pătrată - un subset al planului complex. Procesul iterativ continuă până când Z nu va depăși cercul cu raza 2, al cărui centru se află în punctul (0,0), (aceasta înseamnă că atractorul sistemului dinamic este la infinit) sau după un număr suficient de mare de iterații (de exemplu , 200-500) Z va converge într-un anumit punct al cercului. În funcţie de numărul de iteraţii în timpul cărora Z rămas în interiorul cercului, puteți seta culoarea punctului C(Dacă Z rămâne în interiorul cercului pentru un număr suficient de mare de iterații, procesul de iterație se oprește și acest punct raster este vopsit în negru).

3. Fractali stocastici

O altă clasă binecunoscută de fractali sunt fractalii stocastici, care se obțin dacă unii dintre parametrii săi sunt modificați aleatoriu într-un proces iterativ. În acest caz, obiectele rezultate sunt foarte asemănătoare cu cele naturale - copaci asimetrici, coaste accidentate etc. Fractalii stocastici bidimensionali sunt utilizați în modelarea terenului și a suprafeței mării.
Există și alte clasificări ale fractalilor, de exemplu, împărțirea fractalilor în determiniști (algebrici și geometrici) și nedeterminiști (stochastici).

Despre utilizarea fractalilor

În primul rând, fractalii sunt un domeniu al artei matematice uimitoare, când cu ajutorul celor mai simple formule și algoritmi se obțin imagini de o frumusețe și o complexitate extraordinară! Frunzele, copacii și florile sunt adesea vizibile în contururile imaginilor construite.

Unele dintre cele mai puternice aplicații ale fractalilor se află în grafica computerizată. În primul rând, aceasta este compresia fractală a imaginilor și, în al doilea rând, construcția de peisaje, copaci, plante și generarea de texturi fractale. Fizica și mecanica modernă abia încep să studieze comportamentul obiectelor fractale. Și, desigur, fractalii sunt folosiți direct în matematică în sine.
Avantajele algoritmilor de compresie a imaginilor fractale sunt dimensiunea foarte mică a fișierului împachetat și timpul scurt de recuperare a imaginii. Imaginile fractale împachetate pot fi scalate fără a provoca pixelări. Dar procesul de compresie durează mult și uneori durează ore întregi. Algoritmul de ambalare cu pierderi fractale vă permite să setați raportul de compresie, similar cu formatul jpeg. Algoritmul se bazează pe căutarea unor bucăți mari din imagine care sunt similare cu unele bucăți mici. Și numai piesa care este similară cu care este scrisă în fișierul de ieșire. La comprimare se folosește de obicei o grilă pătrată (piesele sunt pătrate), ceea ce duce la o ușoară angularitate la restaurarea imaginii; o grilă hexagonală nu are acest dezavantaj.
Iterated a dezvoltat un nou format de imagine, „Sting”, care combină compresia fractală și „wave” (cum ar fi jpeg) fără pierderi. Noul format vă permite să creați imagini cu posibilitatea de scalare ulterioară de înaltă calitate, iar volumul fișierelor grafice este de 15-20% din volumul imaginilor necomprimate.
Tendința fractalilor de a semăna cu munți, flori și copaci este exploatată de unii editori grafici, de exemplu, norii fractali din studioul 3D MAX, munții fractali din World Builder. Arborii fractali, munții și peisajele întregi sunt definite prin formule simple, sunt ușor de programat și nu se rup în triunghiuri și cuburi separate atunci când sunt abordate.
Nu se poate ignora utilizarea fractalilor în matematică în sine. În teoria mulțimilor, mulțimea Cantor dovedește existența unor mulțimi perfecte nicăieri dense; în teoria măsurării, funcția autoafină „Scara lui Cantor” este un bun exemplu de funcție de distribuție a unei măsuri singulare.
În mecanică și fizică, fractalii sunt folosiți datorită proprietății lor unice de a repeta contururile multor obiecte naturale. Fractalii vă permit să aproximați copacii, suprafețele de munte și crăpăturile cu o precizie mai mare decât aproximările folosind seturi de segmente sau poligoane (cu aceeași cantitate de date stocate). Modelele fractale, ca și obiectele naturale, au o „rugozitate”, iar această proprietate este păstrată indiferent de cât de mare este mărirea modelului. Prezența unei măsuri uniforme pe fractali permite să se aplice integrarea, teoria potențialului și să le folosească în locul obiectelor standard în ecuațiile deja studiate.
Cu o abordare fractală, haosul încetează să mai fie dezordine albastră și capătă o structură fină. Știința fractală este încă foarte tânără și are un viitor mare în față. Frumusețea fractalilor este departe de a fi epuizată și încă ne va oferi multe capodopere - cele care încântă ochiul și cele care aduc adevărată plăcere minții.

Despre construirea de fractali

Metoda aproximării succesive

Privind această imagine, nu este dificil să înțelegeți cum puteți construi un fractal auto-similar (în acest caz, piramida Sierpinski). Trebuie să luăm o piramidă obișnuită (tetraedru), apoi să-i tăiem mijlocul (octaedru), rezultând patru piramide mici. Cu fiecare dintre ele executam aceeasi operatie etc. Aceasta este o explicație oarecum naivă, dar clară.

Să luăm în considerare esența metodei mai strict. Să existe un sistem IFS, de ex. sistem de cartografiere prin compresie S=(S 1 ,...,S m ) S i:R n ->R n (de exemplu, pentru piramida noastră mapările arată ca S i (x )=1/2*x+o i , unde o i sunt vârfurile tetraedrului, i=1,..,4). Apoi alegem o mulțime compactă A 1 în R n (în cazul nostru alegem un tetraedru). Și determinăm prin inducție șirul mulțimilor A k:A k+1 =S 1 (A k ) U...U S m (A k ). Se știe că mulțimile A k cu k crescând aproximează din ce în ce mai bine atractorul dorit al sistemului S.

Rețineți că fiecare dintre aceste iterații este un atractor sistem recurent de funcții iterate(termen englez Digraf IFS, RIFS Si deasemenea Dirijate grafic IFS) și, prin urmare, sunt ușor de construit folosind programul nostru.

Metodă punct cu punct sau probabilistică

Aceasta este cea mai simplă metodă de implementat pe un computer. Pentru simplitate, luăm în considerare cazul unui set plat autoafin. Deci, fie (S 1,..,S m) un sistem de contracții afine. Mapările S i sunt reprezentabile sub forma: S i (x)=A i (x-o i)+o i, unde A i este o matrice fixă ​​de dimensiune 2x2 și o i este un vector coloană bidimensional.

· Să luăm ca punct de plecare punctul fix al primei mapări S 1:
x : = o1;
Aici profităm de faptul că toate punctele fixe de compresie S 1 ,..,S m aparțin fractalului. Puteți selecta un punct arbitrar ca punct de plecare și secvența de puncte generată de acesta va fi desenată într-un fractal, dar apoi mai multe puncte suplimentare vor apărea pe ecran.

· Să marchem punctul curent x= (x 1 ,x 2) pe ecran:
putpixel(x 1 ,x 2 ,15);

· Să alegem la întâmplare un număr j de la 1 la m și să recalculăm coordonatele punctului x:
j:=aleatoriu (m)+1;
x:=S j (x);

· Trecem la pasul 2 sau, dacă am făcut un număr suficient de mare de iterații, ne oprim.
Notă. Dacă rapoartele de compresie ale mapărilor S i sunt diferite, atunci fractalul va fi umplut cu puncte inegal. Dacă mapările S i sunt similare, acest lucru poate fi evitat complicând ușor algoritmul. Pentru aceasta, la pasul 3 al algoritmului, numărul j de la 1 la m trebuie ales cu probabilități p 1 =r 1 s,..,p m =r m s, unde r i reprezintă coeficienții de compresie ai mapărilor Si, și numărul s (numit dimensiunea asemănării) se găsește din ecuația r 1 s +...+r m s =1. Soluția acestei ecuații poate fi găsită, de exemplu, prin metoda lui Newton.

Despre fractali și algoritmii lor

Fractal provine de la adjectivul latin „fractus”, iar în traducere înseamnă format din fragmente, iar verbul latin corespunzător „frangere” înseamnă a rupe, adică a crea fragmente neregulate. Conceptele de geometrie fractală și fractală, care au apărut la sfârșitul anilor '70, au devenit ferm stabilite în rândul matematicienilor și programatorilor încă de la mijlocul anilor '80. Termenul a fost inventat de Benoit Mandelbrot în 1975 pentru a se referi la structurile neregulate, dar auto-asemănătoare cu care era preocupat. Nașterea geometriei fractale este de obicei asociată cu publicarea cărții lui Mandelbrot „Geometria fractală a naturii” în 1977. Lucrările sale au folosit rezultatele științifice ale altor oameni de știință care au lucrat în perioada 1875-1925 în același domeniu (Poincaré, Fatou, Julia, Cantor, Hausdorff).

Ajustări

Permiteți-mi să fac câteva ajustări la algoritmii propuși în cartea lui H.-O. Peitgen și P.H. Richter „The Beauty of Fractals” M. 1993 pur și simplu pentru a eradica greșelile de scriere și a facilita înțelegerea proceselor, deoarece, după ce le-am studiat, multe au rămas un mister pentru mine. Din păcate, acești algoritmi „de înțeles” și „simpli” duc un stil de viață zguduitor.

Construcția fractalilor se bazează pe o anumită funcție neliniară a unui proces complex cu feedback z = > z 2 +c deoarece z și c -k sunt numere complexe, atunci z = x + iy , c = p + iq este necesar să se descompuneți-l în x și y pentru a merge într-un plan mai realist pentru omul de rând:

x(k+1)=x(k) 2 -y(k) 2 + p,
y(k+1)=2*x(k)*y(k) + q.

Un plan format din toate perechile (x,y ) poate fi considerat ca pentru valori fixe R și q, și cu cele dinamice. În primul caz, parcurgând toate punctele (x ,y) planuri și colorarea acestora în funcție de numărul de repetări de funcție necesare ieșirii din procesul iterativ sau necolorarea lor (culoare neagră) când se depășesc repetările maxime admise, obținem o mapare a mulțimii Julia. Dacă, dimpotrivă, determinăm perechea inițială de valori (x,y) și urmărim soarta ei coloristică cu valorile variabile dinamice ale parametrilor p și q, atunci obținem imagini numite mulțimi Mandelbrot.

Pe problema algoritmilor pentru colorarea fractalilor.

De obicei corpul unui set este reprezentat ca un câmp negru, deși este evident că culoarea neagră poate fi înlocuită cu oricare alta, dar acesta este și un rezultat puțin interesant. Obținerea unei imagini a unui set colorat în toate culorile este o sarcină care nu poate fi rezolvată folosind operații ciclice deoarece numărul de iterații ale mulțimilor care formează corpul este egal cu maximul posibil și este întotdeauna același. Este posibil să colorați un set în culori diferite folosind rezultatul verificării condiției de ieșire a buclei (z_magnitude) sau ceva similar cu acesta, dar cu alte operații matematice, ca număr de culoare.

Aplicarea unui „microscop fractal”

pentru a demonstra fenomene de limită.

Atractorii sunt centre care conduc lupta pentru dominație în avion. Între atractori apare o graniță, reprezentând un model înflorit. Prin creșterea scării de considerație în limitele mulțimii, se pot obține modele non-triviale care reflectă starea de haos determinist - un fenomen comun în lumea naturală.

Obiectele studiate de geografi formează un sistem cu granițe foarte complex organizate și, prin urmare, identificarea lor nu devine o sarcină practică simplă. Complexele naturale au nuclee de tipicitate care acționează ca atractori care își pierd influența asupra teritoriului pe măsură ce acesta se îndepărtează.

Folosind un microscop fractal pentru seturile Mandelbrot și Julia, se poate forma o idee despre procesele și fenomenele limită care sunt la fel de complexe, indiferent de scara de considerare și, astfel, pregătește percepția specialistului pentru o întâlnire cu un obiect natural dinamic și aparent haotic. în spațiu și timp, pentru o înțelegere a naturii geometriei fractale. Culorile multicolore și muzica fractală vor lăsa cu siguranță o amprentă profundă în mintea elevilor.

Mii de publicații și resurse vaste de internet sunt dedicate fractalilor, dar pentru mulți specialiști departe de informatică, acest termen pare cu totul nou. Fractalii, ca obiecte de interes pentru specialiști în diverse domenii ale cunoașterii, ar trebui să primească un loc cuvenit în cursurile de informatică.

Exemple

SIEPINSKI GRID

Acesta este unul dintre fractalii cu care Mandelbrot a experimentat atunci când a dezvoltat conceptele de dimensiuni și iterații fractale. Triunghiurile formate prin conectarea punctelor medii ale unui triunghi mai mare sunt tăiate din triunghiul principal, formând un triunghi cu mai multe găuri. În acest caz, inițiatorul este triunghiul mare, iar șablonul este operația de tăiere a triunghiurilor similare cu cel mai mare. De asemenea, puteți obține o versiune tridimensională a unui triunghi folosind un tetraedru obișnuit și tăind tetraedre mici. Dimensiunea unui astfel de fractal este ln3/ln2 = 1,584962501. A obtine covor Sierpinski, luați un pătrat, împărțiți-l în nouă pătrate și tăiați-l pe cel din mijloc. La fel vom face și cu restul, pătrate mai mici. În cele din urmă, se formează o rețea fractală plată, fără zonă, dar cu conexiuni infinite. În forma sa spațială, buretele Sierpinski este transformat într-un sistem de forme end-to-end, în care fiecare element end-to-end este înlocuit constant cu propriul său fel. Această structură este foarte asemănătoare cu o secțiune de țesut osos. Într-o zi, astfel de structuri care se repetă vor deveni un element al structurilor de construcție. Statica și dinamica lor, crede Mandelbrot, merită studiate îndeaproape.

FRACTAL SIERPINSKI

Nu confundați acest fractal cu rețeaua Sierpinski. Acestea sunt două obiecte complet diferite. În acest fractal, inițiatorul și generatorul sunt la fel. La fiecare iterație, o copie mai mică a inițiatorului este adăugată în fiecare colț al generatorului și așa mai departe. Dacă s-ar efectua un număr infinit de iterații la crearea acestui fractal, acesta ar ocupa întregul plan, fără a lăsa o singură gaură. Prin urmare, dimensiunea sa fractală este ln9/ln3 = 2,0.

CURBA KOCH

Curba Koch este unul dintre cei mai tipici fractali determiniști. A fost inventat în secolul al XIX-lea de un matematician german pe nume Helge von Koch, care, în timp ce studia lucrările lui Georg Kontor și Karl Weierstrasse, a dat peste descrieri ale unor curbe ciudate cu un comportament neobișnuit. Inițiatorul este o linie dreaptă. Generatorul este un triunghi echilateral, ale cărui laturi sunt egale cu o treime din lungimea segmentului mai mare. Aceste triunghiuri sunt adăugate la mijlocul fiecărui segment din nou și din nou. În cercetările sale, Mandelbrot a experimentat intens cu curbele Koch și a produs figuri precum Insulele Koch, Crucile Koch, Fulgii de zăpadă Koch și chiar reprezentări tridimensionale ale curbei Koch, folosind un tetraedru și adăugând tetraedre mai mici la fiecare dintre fețele sale. Curba Koch are dimensiunea ln4/ln3 = 1,261859507.

FRACTAL MANDELBROT

Acesta NU este setul Mandelbrot, pe care îl vedeți destul de des. Mulțimea Mandelbrot se bazează pe ecuații neliniare și este un fractal complex. Aceasta este, de asemenea, o variantă a curbei Koch, deși acest obiect nu este similar cu acesta. Inițiatorul și generatorul sunt, de asemenea, diferite de cele folosite pentru a crea fractali bazați pe principiul curbei Koch, dar ideea rămâne aceeași.În loc să unească triunghiuri echilaterale cu un segment de curbă, pătratele sunt unite cu un pătrat. Datorită faptului că acest fractal ocupă exact jumătate din spațiul alocat la fiecare iterație, are o dimensiune fractală simplă de 3/2 = 1,5.

FRACTALELE STEA ȘI FULGUL DE ZĂpadă

Ambele obiecte nu sunt fractali clasici și nu au fost inventate de Mandelbrot sau de orice alt matematician celebru. Tocmai am creat acești fractali din interes și pentru a experimenta programarea. Atât inițiatorul, cât și generatorul de aici sunt o figură formată prin conectarea punctelor de mijloc ale laturilor cu punctele de mijloc ale laturilor opuse într-un hexagon obișnuit. Mai mult, nu pot decât să bănuiesc dimensiunea acestor fractali.

PENTAGON MAI ÎNDRAZĂT

Un fractal arată ca o grămadă de pentagoane strânse împreună. De fapt, se formează prin utilizarea unui pentagon ca inițiator și a triunghiurilor isoscele în care raportul dintre latura mai mare și latura mai mică este exact egal cu așa-numitul raport de aur (1,618033989 sau 1/(2cos72)) ca generator. . Aceste triunghiuri sunt tăiate de la mijlocul fiecărui pentagon, rezultând o formă care arată ca 5 pentagoane mici lipite de unul mare. O variantă a acestui fractal poate fi obținută prin utilizarea unui hexagon ca inițiator. Acest fractal se numește Steaua lui David și este destul de asemănător cu o versiune hexagonală a fulgului de zăpadă Koch. Dimensiunea fractală a pentagonului Darer este ln6/ln (1+g), unde g este raportul dintre lungimea laturii mai mari a triunghiului și lungimea celei mai mici. În acest caz, g este raportul de aur, deci dimensiunea fractală este de aproximativ 1,86171596. Dimensiunea fractală a Stelei lui David ln6/ln3 sau 1,630929754.

CURBA HILBERT

Acest fractal este foarte asemănător cu Fractalul Labirint, cu excepția faptului că lățimea literei U, care este generatorul, nu se schimbă cu fiecare iterație. Cu toate acestea, spre deosebire de Fractalul Labirint, curba Hilbert, numită și Hotelul Hilbert, are o singură dimensiune fractală, care este exact 2,0, deoarece cu un număr infinit de iterații, va ocupa întregul plan. fractal și apoi faceți același lucru cu o zonă mică din acea zonă, cele două măriri vor fi semnificativ diferite una de cealaltă. Cele două imagini vor fi foarte asemănătoare în detaliu, dar nu vor fi complet identice. Figura 1. Aproximarea mulțimii Mandelbrot Comparați, de exemplu, imaginile setului Mandelbrot prezentate aici, dintre care una a fost obținută prin mărirea unei anumite zone a celeilalte. După cum puteți vedea, ele nu sunt absolut identice, deși pe ambele vedem un cerc negru, din care tentaculele în flăcări se extind în direcții diferite. Aceste elemente se repetă la nesfârșit în setul Mandelbrot în proporții descrescătoare. Fractalii determiniști sunt liniari, în timp ce fractalii complexi nu sunt. Fiind neliniari, acești fractali sunt generați de ceea ce Mandelbrot a numit ecuații algebrice neliniare. Un bun exemplu este procesul Zn+1=ZnI + C, care este ecuația folosită pentru a construi mulțimea Mandelbrot și Julia de gradul doi. Rezolvarea acestor ecuații matematice implică numere complexe și imaginare. Când ecuația este interpretată grafic în plan complex, rezultă o figură ciudată în care liniile drepte devin curbe și apar efecte de auto-asemănare, deși nu fără deformații, la diferite niveluri de scară. În același timp, întreaga imagine în ansamblu este imprevizibilă și foarte haotică. După cum puteți vedea uitându-vă la imagini, fractalii complexi sunt într-adevăr foarte complexi și nu pot fi creați fără ajutorul unui computer. Pentru a obține rezultate pline de culoare, acest computer trebuie să aibă un coprocesor matematic puternic și un monitor de înaltă rezoluție. Spre deosebire de fractalii determiniști, fractalii complecși nu sunt calculati în 5-10 iterații. Aproape fiecare punct de pe ecranul unui computer este ca un fractal separat. În timpul procesării matematice, fiecare punct este tratat ca un desen separat. Fiecare punct corespunde unei anumite valori. Ecuația este încorporată pentru fiecare punct și se efectuează, de exemplu, 1000 de iterații. Pentru a obține o imagine relativ nedistorsionată într-o perioadă de timp acceptabilă pentru computerele de acasă, este posibil să se efectueze 250 de iterații pentru un punct. Majoritatea fractalilor pe care îi vedem astăzi sunt frumos colorați. Poate că imaginile fractale capătă o semnificație estetică atât de mare tocmai datorită schemelor lor de culori. După ce ecuația este calculată, computerul analizează rezultatele. Dacă rezultatele rămân stabile sau fluctuează în jurul unei anumite valori, punctul devine de obicei negru. Dacă valoarea la un pas sau altul tinde spre infinit, punctul este vopsit într-o culoare diferită, poate albastru sau roșu. În timpul acestui proces, computerul atribuie culori tuturor vitezelor de mișcare. De obicei, punctele care se mișcă rapid sunt colorate în roșu, în timp ce cele mai lente sunt colorate în galben și așa mai departe. Petele întunecate sunt probabil cele mai stabile. Fractalii complexi sunt diferiti de determinatîn sensul că sunt infinit de complexe, dar în același timp pot fi generate printr-o formulă foarte simplă. Fractalii determiniști nu necesită formule sau ecuații. Luați doar niște hârtie de desen și puteți construi o sită Sierpinski de până la 3 sau 4 iterații fără nicio dificultate. Încearcă asta cu multă Julia! Este mai ușor să măsori lungimea coastei Angliei! SET MANDELBROT Fig 2. Mulțimea Mandelbrot Seturile Mandelbrot și Julia sunt probabil cele mai comune dintre fractalii complecși. Acestea pot fi găsite în multe reviste științifice, coperți de cărți, cărți poștale și economizor de ecran de computer. Setul Mandelbrot, care a fost construit de Benoit Mandelbrot, este probabil prima asociere pe care oamenii o au atunci când aud cuvântul fractal. Acest fractal, care seamănă cu o mașină de cardare cu zone circulare și asemănătoare arborilor în flăcări atașate la el, este generat de formula simplă Zn+1=Zna+C, unde Z și C sunt numere complexe și a este un număr pozitiv. Mulțimea Mandelbrot, care poate fi văzută cel mai adesea, este mulțimea Mandelbrot de gradul 2, adică a = 2. Faptul că mulțimea Mandelbrot nu este doar Zn+1=ZnІ+C, ci un fractal, al cărui indicator în formula poate fi orice număr pozitiv, i-a indus în eroare pe mulți. Pe această pagină vedeți un exemplu de set Mandelbrot pentru diferite valori ale exponentului a. Figura 3. Aspectul bulelor la a=3,5 Procesul Z=Z*tg (Z+C) este de asemenea popular. Prin includerea funcției tangente, rezultatul este un set Mandelbrot înconjurat de o zonă asemănătoare unui măr. Când se utilizează funcția cosinus, se obțin efecte de bule de aer. Pe scurt, există un număr infinit de moduri de a configura setul Mandelbrot pentru a produce diferite imagini frumoase. MULTE JULIA În mod surprinzător, mulțimile Julia sunt formate folosind aceeași formulă ca și mulțimea Mandelbrot. Setul Julia a fost inventat de matematicianul francez Gaston Julia, după care a fost numit setul. Prima întrebare care apare după o cunoaștere vizuală cu mulțimile Mandelbrot și Julia este „dacă ambii fractali sunt generați conform aceleiași formule, de ce sunt atât de diferiți?” Priviți mai întâi pozele cu setul Julia. Destul de ciudat, există diferite tipuri de seturi Julia. Când desenați un fractal folosind diferite puncte de plecare (pentru a începe procesul de iterație), sunt generate imagini diferite. Acest lucru se aplică numai setului Julia. Figura 4. Setul Julia Deși nu poate fi văzut în imagine, un fractal Mandelbrot este de fapt mulți fractali Julia conectați împreună. Fiecare punct (sau coordonată) al mulțimii Mandelbrot corespunde unui fractal Julia. Seturile Julia pot fi generate folosind aceste puncte ca valori inițiale în ecuația Z=ZI+C. Dar acest lucru nu înseamnă că, dacă selectați un punct pe fractalul Mandelbrot și îl măriți, puteți obține fractalul Julia. Aceste două puncte sunt identice, dar numai în sens matematic. Dacă luați acest punct și îl calculați folosind această formulă, puteți obține fractalul Julia, corespunzător unui anumit punct al fractalului Mandelbrot.