Зависимость разности потенциалов от расстояния. Разность потенциалов, энергия заряда в электрическом поле. Потенциал
В предыдущем параграфе мы обсуждали основную характеристику электрического поля – его напряжённость. Как следует из самого определения – это силовая характеристика, а значит векторная. В ряде случаев более удобными являются скалярные характеристики, которые, оказывается, тоже можно ввести для электростатического поля – разность потенциалов и потенциал. При этом мы будем опираться на важное фундаментальное свойство сил, действующих на заряд в электростатическом поле – их консервативность.
Напомним, что консервативными называются силы, работа которых не зависит от формы траектории движения тела. Работа таких сил определяется лишь координатами начальной и конечной точек перемещения. Опираясь на наши знания свойств его силовых характеристик электростатического поля, созданного произвольной системой зарядов, можно было бы провести подробное доказательство равенства работ при движении заряда между любыми двумя его точками. Но мы несколько сократим эту процедуру, вспомнив теорему «о консервативности центральных сил», доказанную нами в разделе механика.
Неподвижный точечный заряд является источником «поля центральных сил» – это прямо следует из формулировки основного закона электростатики – закона Кулона. Из принципа суперпозиции электрических полей следует, что работа при перемещении пробного заряда в поле любой системы покоящихся зарядов является алгебраической суммой работ в поле каждого из зарядов в отдельности. А значит поле таких сил («кулоновских сил»*)) также является полем сил консервативных. Это и требовалось доказать.
Таким образом, работа сил электростатического поля **) по перемещению точечного (пробного) заряда между двумя точками характеризует это поле. Но она зависит и от величины пробного заряда q 0 . Об этом говорит опыт, но это понятно и, исходя из наших знаний о «кулоновских» силах. Ведь они пропорциональны заряду q 0 в каждой точке траектории 1®2 (исходя из закона Кулона), а работа пропорциональна силе. Чтобы охарактеризовать поле и только поле можно поделить работу на величину пробного заряда. То, что получится и есть «разность потенциалов». Приведём определение этого важного понятия:
(Опр .) Разностью потенциалов между точками электростатического поля 1 и 2 называется отношение работы поля по перемещению пробного заряда из точки 1 в точку 2 к величине этого заряда :
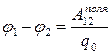 . (3.1)
. (3.1)
В системе СИ единица измерения разности потенциалов называется 1 вольт (1 В = 1 Дж/Кл). Если мы научимся каким-либо образом определять разность потенциалов j 1 –j 2 для поля системы покоящихся зарядов (теоретически или экспериментально), то это позволит находить работу поля по перемещению любого точечного заряда q в этом поле:
![]() . (3.2)
. (3.2)
Таким образом, разность потенциалов это энергетическая характеристика электрического поля, поскольку связана непосредственно с понятием работы.
В механике мы вводили для консервативных сил (сейчас мы, скажем: «полей консервативных сил») понятие «потенциальная энергия». При этом мы руководствовались следующим принципом: «работа сил поля равна убыли потенциальной энергии». Формализуем этот принцип в аналитической записи:
Здесь U 1 и U 2 – потенциальная энергия в «начальном» («1») и «конечном» («2») состояниях системы соответственно. В обсуждаемом случае поля системы неподвижных зарядов – это энергия точечного заряда q в положении «1» (с координатами {x 1 ,y 1 ,z 1 }) и положении «2» (с координатами {x 2 ,y 2 ,z 2 }) электростатического поля. Т.е. потенциальная энергия заряда в этом поле – скалярная функция координат точек поля U = U(x ,y ,z ) (или ). Сравнивая (3.2) и (3.3), видим – удобно считать, что разность потенциалов представляет собой разность значений ещё одной скалярной функции координат точек поля j (x,y,z ). Она связана с функцией U(x ,y ,z ) (потенциальной энергией) простым соотношением: U(x ,y ,z ) = q ×j (x,y,z ). Или, поскольку
говорят, что она «численно равна потенциальной энергии единичного положительного заряда» в данной точке поля. И называется эта величина j «потенциал» данной точки электростатического поля.
Самое важное заключается в том, как найти эту функцию для поля конкретной системы зарядов? Какова процедура действий?
Прежде всего, придётся договориться об условиях нормировки*): надо выбрать точку Р 0 , в которой потенциал пробного заряда будем полагать равным нулю . Чаще всего такую точку выбирают «бесконечно» удалённой, там где поле отсутствует **). Для этого надо найти «удельную» работу поля –т.е. работу, отнесённую к величине переносимого пробного заряда (или, как нередко говорят, «по перемещению единичного положительного» заряда) из данной точки поля Р (x ,y ,z ) в точку нормировки Р 0 . В аналитической форме это определение потенциала можно записать так:
(Опр. ) j Р (x ,y ,z ) = . (3.5)
Нельзя ли выразить вновь введённые нами величины – разность потенциалов и потенциал через силовую характеристику, которую мы уже научились рассчитывать по заданному расположению зарядов в пространстве? Конечно можно. Запишем цепочку хорошо понятных нам равенств:
 .
.
Выпишем последнее равенство ещё раз
 . (3.6)
. (3.6)
Оно даёт «рецепт» поиска разности потенциалов по известной функции напряжённости. Аналогично для потенциала:
И окончательно для потенциала произвольной точки поля Р с координатами (x ,y ,z ):
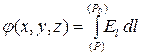 . (3.7)
. (3.7)
· Потенциал поля точечного заряда
Опираясь на процедуру расчёта потенциала, получим выражение для случая поля точечного заряда. Это очень важно для дальнейших расчётов потенциала поля системы произвольно расположенных в пространстве зарядов.
2. Выбор траектории. Пусть произвольная точка Р (x ,y ,z ) находится на расстоянии r от заряда-источника. Поскольку результат не зависит от формы траектории для расчёта криволинейного интеграла вида (3.7) выберем простейшую радиально направленную прямую из данной точки поля вдоль силовой линии и «уходящую в бесконечность».
3. Расчёт . В соответствии с определением потенциала выполним расчёт «удельной» работы поля созданного точечным зарядом q по переносу пробного заряда вдоль выбранной траектории. Нижеприводимая цепочка равенств, надеемся, выглядит достаточно «прозрачно». Однако дадим к ней всё же минимальный комментарий. Прежде всего, отметим, что в силу нашего выбора траектории в виде радиально направленного от заряда луча можно обозначения E l и dl (произвольная кривая «L ») поменять на E r и dr (полярная ось «r »). Более того, поскольку вектор направлен радиально, для любого малого перемещения вдоль траектории проекция вектора напряжённости равна просто модулю этого вектора E (r ). В итоге и мы можем сделать важный шаг в нашем расчёте – совершить переход от криволинейного интеграла к обычному определённому:
 .*)
.*)
Теперь после подстановки выражения для модуля напряжённости поля точечного заряда (3.5) нам остаётся всего лишь математическая «рутина»:
Выпишем результат ещё раз, дополнив его учётом возможного наличия газообразной или жидкой однородной диэлектрической среды с проницаемостью e , заполняющей всё окружающее точечный заряд пространство:
 . (3.8)
. (3.8)
Потенциал поля точечного заряда, как видим, убывает с расстоянием по закону 1/r .
· Эквипотенциальные поверхности
При обсуждении силовой характеристики электростатического поля мы убедились в плодотворности понятия силовых линий (линий напряжённости). Для энергетической характеристики поля – потенциала – полезно также ввести дополнительную иллюстративную характеристику – систему «эквипотенциальных поверхностей». Из самого названия ясно («экви» означает «равный»), что это поверхности постоянного потенциала, которые характеризуют способность сил поля совершать работу при перемещении заряда. Вдоль таких поверхностей работа, очевидно, вообще не совершается. Она максимальна по направлениям, по которым максимальна густота (плотность) расположения эквипотенциальных поверхностей. В этих местах максимальна и напряжённость поля. Нетрудно сообразить, какова и взаимная ориентация силовых линий и эквипотенциальных поверхностей в местах их пересечений: они взаимно перпендикулярны . Ведь при любом малом перемещении вдоль эквипотенциальной поверхности элементарная работа равна нулю, а это возможно только в случае, если равна нулю касательная составляющая вектора напряжённости, т.е. он направлен строго по нормали к поверхности. Ниже мы приводим цепочку соответствующих этим словам, надеемся, довольно очевидных равенств:

Вместе с рис. 3. … они доказывают, по сути, уже сформулированное утверждение: силовые линии пересекают (или «подходят к …») эквипотенциальные поверхности под прямым углом !
Приведём картину эквипотенциальных поверхностей (и силовых линий тоже) для некоторых простейших уже хорошо нам знакомых случаев электростатического поля: а ) поле точечного заряда; б ) поле двух одинаковых по модулю разноимённых точечных зарядов; в ) поле между двумя разноимённо заряженными плоскопараллельными большими (по сравнению с расстоянием между ними) пластинами – см. рис. 3.1.
Обратимся
теперь к сферическому (точечному) заряду.
Выше показано, что напряжённость
электрического поля, созданного
равномерно распределённым по сфере
зарядом Q
,
не зависит от радиуса сферы. Представим,
что на некотором расстоянии
r
от
центра сферы находится пробный заряд q
.
Напряжённость поля в точке, где находится
заряд, 
На
рисунке изображён график зависимости
силы электростатического взаимодействия
между точечными зарядами от расстояния
между ними. Чтобы найти работу
электрического поля при перемещении
пробного заряда q
с
расстояния r
до
расстоянияR
,
разобьём этот промежуток
точками r
1 , r
2 ,..., r
п
на
равные отрезки. Средняя сила, действующая
на заряд q
в
пределах отрезка [rr
1 ],
равна ![]()
Работа этой силы на этом участке:
![]()
Аналогичные выражения для работы получатся для всех других участков. Поэтому полная работа:
Одинаковые слагаемые с противоположными знаками уничтожаются, и окончательно получаем:
– работа
поля над зарядом ![]()
– разность
потенциалов ![]()
Теперь, чтобы найти потенциал точки поля относительно бесконечности, устремляем R к бесконечности и окончательно получаем:
Итак, потенциал поля точечного заряда обратно пропорционален расстоянию до заряда.
24. Потенциальная энергия заряда в поле системы зарядов. Принцип суперпозиции для потенциалов. Принцип суперпозиции для потенциалов
Любое как угодно сложное электростатическое поле можно представить в виде суперпозиции полей точечных зарядов. Каждое такое поле в выбранной точке имеет определённый потенциал. Поскольку потенциал является скалярной величиной, результирующий потенциал поля всех точечных зарядов есть алгебраическая сумма потенциалов 1 , 2 , 3 , … полей отдельных зарядов: = 1 + 2 + 3 + ... Это соотношение является прямым следствием принципа суперпозиции электрических полей.
Потенциальная энергия заряда в электрическом поле. Продолжим сравнение гравитационного взаимодействия тел и электростатического взаимодействия зарядов. Тело массой m в поле тяжести Земли обладает потенциальной энергией. Работа силы тяжести равна изменению потенциальной энергии, взятому с противоположным знаком:
A = - (W p2 - W p1 ) = mgh .
(Здесь и далее мы будем обозначать энергию буквой W .) Точно так же, как тело массой m в поле силы тяжести обладает потенциальной энергией, пропорциональной массе тела, электрический заряд в электростатическом поле обладает потенциальной энергией W p , пропорциональной заряду q . Работа сил электростатического поля А равна изменению потенциальной энергии заряда в электрическом поле, взятому с противоположным знаком:
A = - (W p2 - W p1 ) . (40.1)
25. Разность потенциалов. Эквипотенциальные поверхности
Эквипотенциальная поверхность – поверхность, каждая точка которой имеет одинаковый потенциал.
Как следует из связи работы и потенциалов:
при переносе заряда вдоль эквипотенциальных поверхностей электрическое поле работы не совершает, так как .
Работа при ненулевой силе равна нулю только в том случае, если вектор силы перпендикулярен вектору перемещения. Из этого следует, что линии напряженности перпендикулярны эквипотенциальным поверхностям. Примерами эквипотенциальных поверхностей служат сферы для поля точечного заряда и параллельные плоскости для однородных полей (рис. 3).

Разность потенциалов (напряжение) между двумя точками равна отношению работы поля при перемещении заряда из начальной точки в конечную к модулю этого заряда: U = φ 1 - φ 2 = -Δφ = A / q, A = -(W п2 - W п1) = -q(φ 2 - φ 1) = -qΔφ
Разность потенциалов измеряется в вольтах (В = Дж / Кл) Связь между напряжённостью электростатического поля и разностью потенциалов: E x = Δφ / Δx Напряжённость электростатического поля направлена в сторону убывания потенциала. Измеряется в вольтах, делённых на метры (В / м)
§ 15. ПОТЕНЦИАЛ. ЭНЕРГИЯ СИСТЕМЫ ЭЛЕКТРИЧЕСКИХ ЗАРЯДОВ. РАБОТА ПО ПЕРЕМЕЩЕНИЮ ЗАРЯДА В ПОЛЕ
Основные формулы
Потенциал электрического поля есть величина, равная отношению потенциальной энергии точечного положительного заряда, помещенную в данную точку поля, к этому заряду;
=П/Q ,
или потенциал электрического поля есть величина, равная отношению работы сил поля по перемещению точечного положительного заряда из данной точки поля в бесконечность к этому заряду:
=A / Q .
Потенциал электрического поля в бесконечности условно принят равным нулю.
Отметим, что при перемещении заряда в электрическом поле работа A в.с внешних сил равна по модулю работеA с.п сил поля и противоположна ей по знаку:
A в.с = – A с.п .
Потенциал электрического поля, создаваемый точечным зарядом Q на расстоянииr от заряда,
Потенциал электрического поля, создаваемого металлической, несущей заряд Q сферой радиусомR , на расстоянии гот центра сферы:
внутри сферы
(r
<R
)
 ;
;
на поверхности сферы (r =R )
 ;
;
вне сферы (r
>
R
)
 .
.
Во всех приведенных для потенциала заряженной сферы формулах есть диэлектрическая проницаемость однородного безграничного диэлектрика, окружающего сферу.
Потенциал электрического поля, созданного системой п точечных зарядов, в данной точке в соответствии с принципом суперпозиции электрических полей равен алгебраическойсуммепотенциалов 1 , 2 , ... , n , создаваемых отдельными точечными зарядамиQ 1 ,Q 2 , ...,Q n :
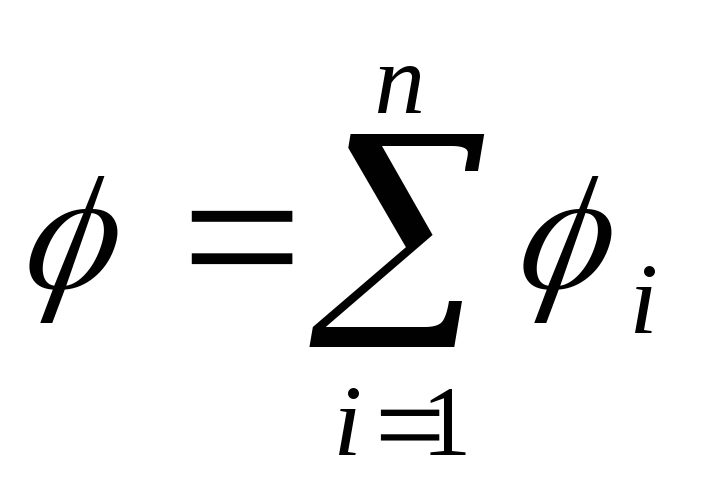
Энергия W взаимодействия системы точечных зарядовQ 1 ,Q 2 , ...,Q n определяется работой, которую эта система зарядов может совершить при удаленииих относительно друг друга в бесконечность, и выражается формулой
 ,
,
где i - потенциал поля, создаваемого всемип– 1 зарядами (за исключением 1-го) в точке, где расположен зарядQ i .
Потенциал связан с напряженностью электрического поля соотношением
Е = –grad.
В случае электрического поля, обладающего сферической симметрией, эта связь выражается формулой
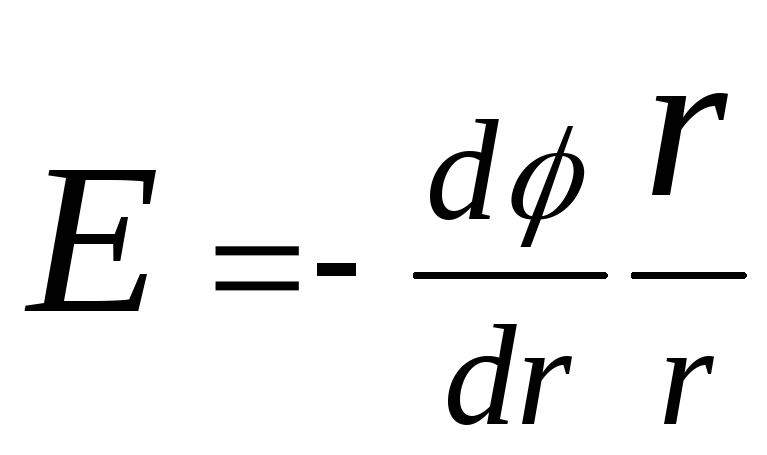 ,
,
или в скалярной форме
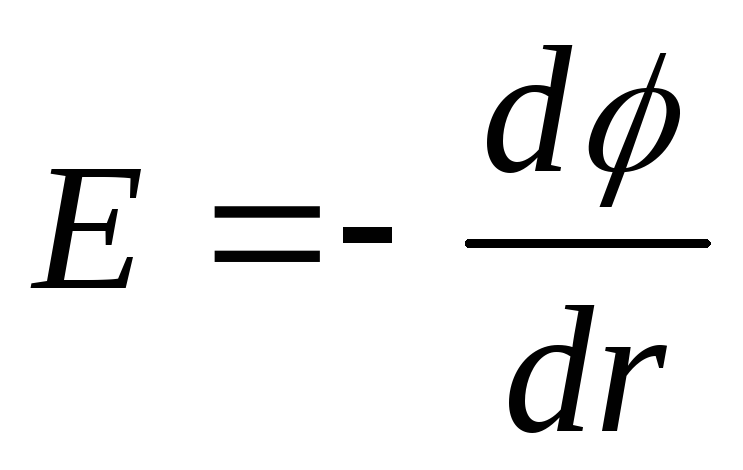 ,
,
а в случае однородного поля, т. е. поля, напряженность которого в каждой точке его одинакова как по модулю, так и по направлению,
E =( 1 – 2 ,)/d ,
где 1 и 2 - потенциалы точек двух эквипотенциальных поверхностей;d - расстояние между этими поверхностями вдоль электрической силовой линии.
Работа, совершаемая электрическим полем при перемещении точечного заряда Q из одной точки поля, имеющей потенциал 1 , в другую, имеющую потенциал 2 ,
A
=Q
( 1
- 2
),
или
 ,
,
где E l - проекция вектора напряженностиЕ на направление перемещения;dl - перемещение.
В случае однородного поля последняя формула принимает вид
A = QElcos ,
где l - перемещение;- угол между направлениями вектораЕ и перемещенияl .
Примеры решения задач
Пример 1. Положительные зарядыQ 1 =3 мкКл иQ 2 =20 нКл находятся в вакууме на расстоянииr 1 =l,5 м друг от друга. Определить работуA , которую надо совершить, чтобы сблизить заряды до расстоянияr 2 =1 м.
Решение. Положим, что первый зарядQ 1 остается неподвижным, а второйQ 2 под действием внешних сил перемещается в поле, созданном зарядомQ 1 , приближаясь к нему с расстоянияr 1 =t,5 м доr 2 =1 м.
Работа А" внешней силы по перемещению зарядаQ из однойточки поля с потенциалом 1 в другую, потенциал которой 2 , равна по модулю и противоположна по знаку работеА сил поля по перемещению заряда между теми же точками:
А"= -А.
Работа А сил поля по перемещению зарядаA =Q ( 1 - 2 ). Тогда работаА" внешних сил может быть записана в виде
A " = –Q ( 1 - 2 )=Q ( 2 - 1 ). (1)
Потенциалы точек начала и конца пути выразятся формулами
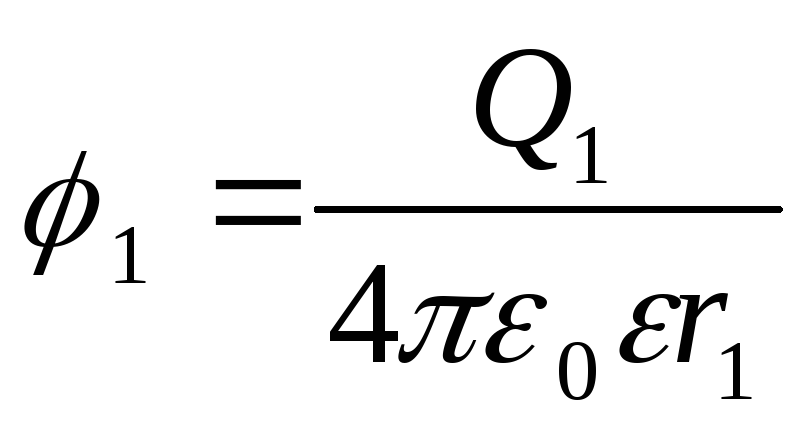 ;
;
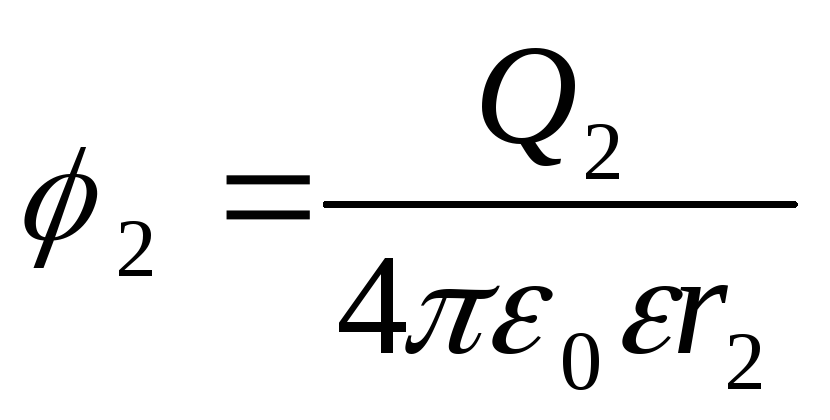 .
.
Подставляя выражения 1 и 2 в формулу (1) и учитывая, что для данного случая переносимый зарядQ =Q 2 , получим
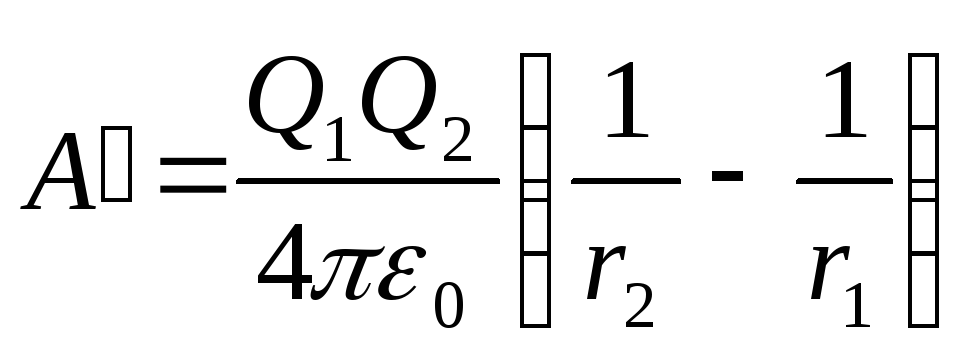 . (2)
. (2)
Если учесть, что 1/(4 0 )=910 9 м/Ф, то после подстановки значений величин в формулу (2) и вычисления найдем
A "=180 мкДж.
Пример 2. Найти работуА поля по перемещению зарядаQ =10 нКл из точки1 в точку2 (рис. 15.1), находящиеся между двумя разноименно заряженными с поверхностной плотностью=0,4 мкКл/м 2 бесконечными параллельными плоскостями, расстояниеl между которыми равно 3 см.
Р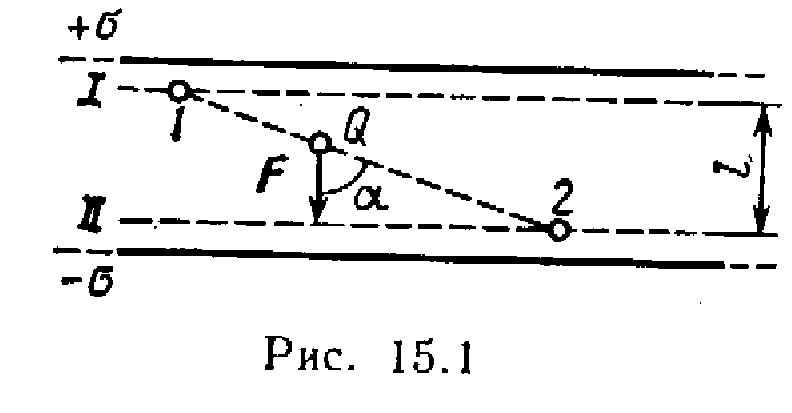 ешение.
Возможны два способа решения задачи.
ешение.
Возможны два способа решения задачи.
1-й способ. Работу сил поля по перемещению заряда Q из точки1 поля с потенциалом 1 в точку2 поля с потенциалом 2 найдем по формуле
A =Q ( 1 - 2 ). (1)
Для определения потенциалов в точках 1 и2 проведем через эти точки эквипотенциальные поверхностиIиII. Эти поверхности будут плоскостями, так как поле между двумя равномерно заряженными бесконечными параллельными плоскостями однородно. Для такого поля справедливо соотношение
1 - 2 =El , (2)
где Е - напряженность поля;l - расстояние между эквипотенциальными поверхностями.
Напряженность поля между параллельными бесконечными разноименно заряженными плоскостями E =/ 0 . Подставив это выражениеЕ в формулу (2) и затем выражение 1 - 2 в формулу (1), получим
A = Q ( / 0 ) l .
2-й способ. Так как поле однородно, то сила, действующая на зарядQ , при его перемещении постоянна. Поэтому работу перемещения заряда из точки1 в точку2 можно подсчитать по формуле
A =F r cos, (3)
где F - сила, действующая на заряд;r - модуль перемещения зарядаQ из точки1 в точку2; - угол между направлениями перемещения и силы. Но F = QE = Q ( / 0 ). Подставив это выражениеF в равенство (3), а также заметив, чтоr cos=l , получим
A =Q (/ 0 )l . (4)
Таким образом, оба решения приводят к одному и тому же результату.
Подставив в выражение (4) значение величин Q , , 0 иl , найдем
A =13,6 мкДж.
Пример 3.
По
тонкой нити, изогнутой по дуге окружности
радиусомR
,
равномерно распределен заряд с линейной
плотностью=10 нКл/м.
Определить напряженностьЕ
и
потенциалэлектрического поля, создаваемого таким
р аспределенным
зарядом в точкеО
, совпадающей с
центром кривизны дуги. Длинаl
нити составляет 1/3 длины окружности и
равна 15 см.
аспределенным
зарядом в точкеО
, совпадающей с
центром кривизны дуги. Длинаl
нити составляет 1/3 длины окружности и
равна 15 см.
Решение. Выберем оси координат так, чтобы начало координат совпадало с центром кривизны дуги, а осьу была симметрично расположена относительно концов дуги (рис. 15.2). На нити выделим элемент длиныdl . ЗарядdQ =dl , находящийся на выделенном участке, можно считать точечным.
Определим напряженность электрического поля в точке О . Для этого найдем сначала напряженностьdE поля, создаваемого зарядомdQ :
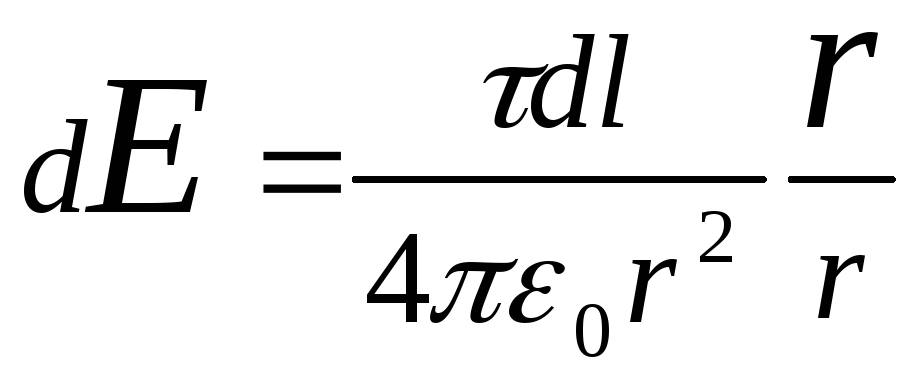 ,
,
где r -радиус-вектор, направленный от элементаdl к точке, напряженность в которой вычисляется. Выразим вектор dE через проекцииdE x c иdE y на оси координат:
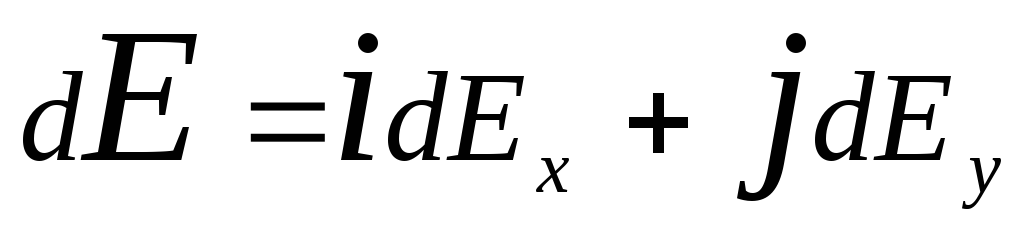 ,
,
где i иj - единичные векторы направлений (орты).
Напряженность Е найдем интегрированием:
 .
.
Интегрирование
ведется вдоль дуги длины l
.
В силу симметрии интеграл
 равен нулю. Тогда
равен нулю. Тогда
 , (1)
, (1)
где
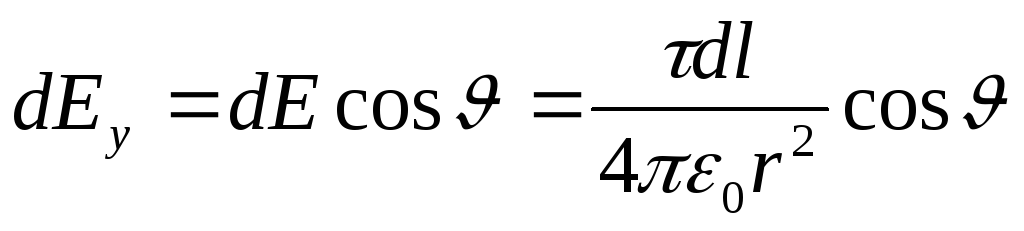 .
Так какr
=R
=constиdl
=R
d.
то
.
Так какr
=R
=constиdl
=R
d.
то
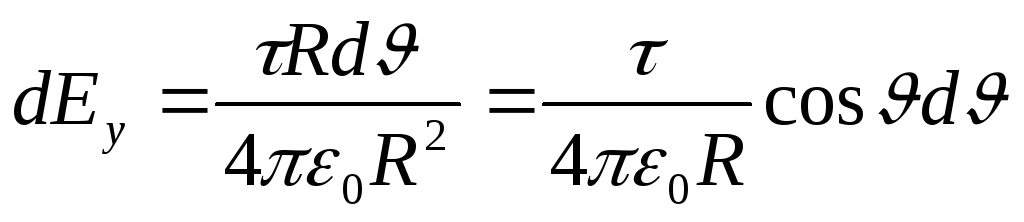
Подставим найденное выражение dE y в (1) и, приняв во внимание симметричное расположение дуги относительно осиОу, пределы интегрирования возьмем от 0 до/3, а результат удвоим;
 .
.
Подставив указанные пределы и выразив R через длину дуги(3 l = 2r ), получим
 .
.
Из этой формулы видно, что вектор Е совпадает с положительным направлением осиОу Подставив значениеиl в последнюю формулу и сделав вычисления, найдем
E =2,18 кВ/м.
Определим потенциал электрического поля в точке О . Найдем сначала потенциалd, создаваемый точечным зарядомdQ в точкеО:

Заменим r наR и произведем интегрирование:
 .Так
как l
=2
R
/3,
то
.Так
как l
=2
R
/3,
то
=/(6 0 ).
Произведя вычисления по этой формуле, получим
Пример 4 . Электрическое поле создана длинным цилиндром радиусомR = 1см, равномерно заряженным с линейной плотностью=20 нКл/м. Определить разность потенциалов двух точек этого поля, находящихся на расстоянияхa 1 =0,5 см иа 2 =2 см от поверхности цилиндра, в средней его части.
Решение. Для определения разности потенциалов воспользуемся соотношением между напряженностью поля и изменением потенциалаЕ = -grad. Для поля с осевой симметрией, каким является поле цилиндра, это соотношение можно записать в виде
Е= –(d/dr ) , илиd= -Е dr .
Интегрируя последнее выражение, найдем разность потенциалов двух точек, отстоящих на r 1 иr 2 от оси цилиндра;
![]() . (1)
. (1)
Так как цилиндр
длинный и точки взяты вблизи его средней
части, то для выражения напряженности
поля можно воспользоваться формулой
 .
Подставив это выражениеЕ
в равенство
(1), получим
.
Подставив это выражениеЕ
в равенство
(1), получим
 (2)
(2)
Так как величины r 2 иr 1 входят в формулу в виде отношения, то их можно выразить в любых, но только одинаковых единицах:
r 1 =R+a 1 = 1,5 см; r 2 =R +a 2 =3см.
Подставив значения величия , 0 ,r 1 иr 2 в формулу (2) и вычислив, найдем
1 - 2 =250 В.
Пример 5. Электрическое поле создано тонким стержнем, несущим равномерно распределенный по длине заряд=0,1 мкКл/м. Определить потенциалполя в точке, удаленной от концов стержня на расстояние, равное длине стержня.
Решение. Заряд, находящийся на стержне, нельзя считать точечным, поэтому непосредственно применить для вычисления потенциала формулу
 , (1)
, (1)
справедливую только для точечных зарядов, нельзя. Но если разбить стержень на элементарные отрезки dl , то зарядdl , находящийся на каждом из них, можно рассматривать как точечный и тогда формула (1) будет справедлива. Применив эту формулу, получим
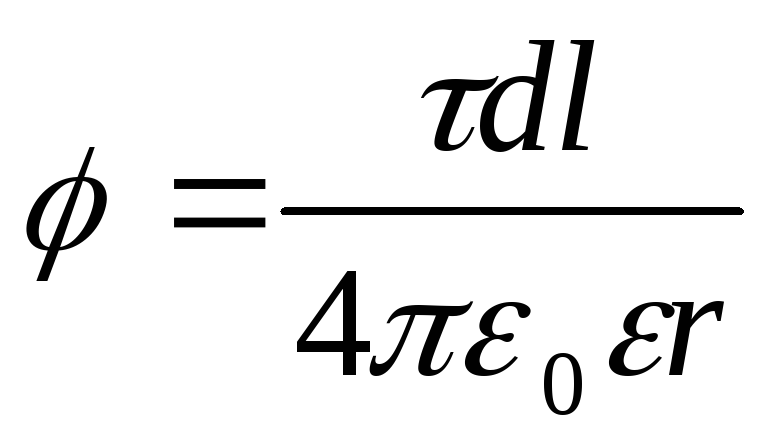 , (2)
, (2)
где r - расстояние точки, в которой определяется потенциал, до элемента стержня.
Из рис. 15.3 следует,
что dl
=(r
d/cos).
Подставив это выражение dl
в формулу (2), найдем .
.
Интегрируя
полученное выражение в пределах от 1
да 2
,
получим потенциал, создаваемый всем
зарядом, распределенным на стержне: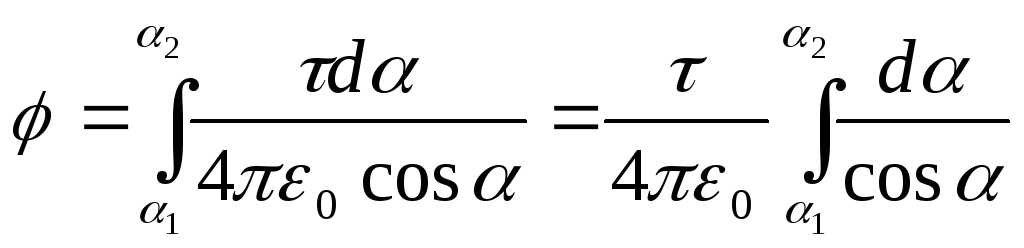 .
.
В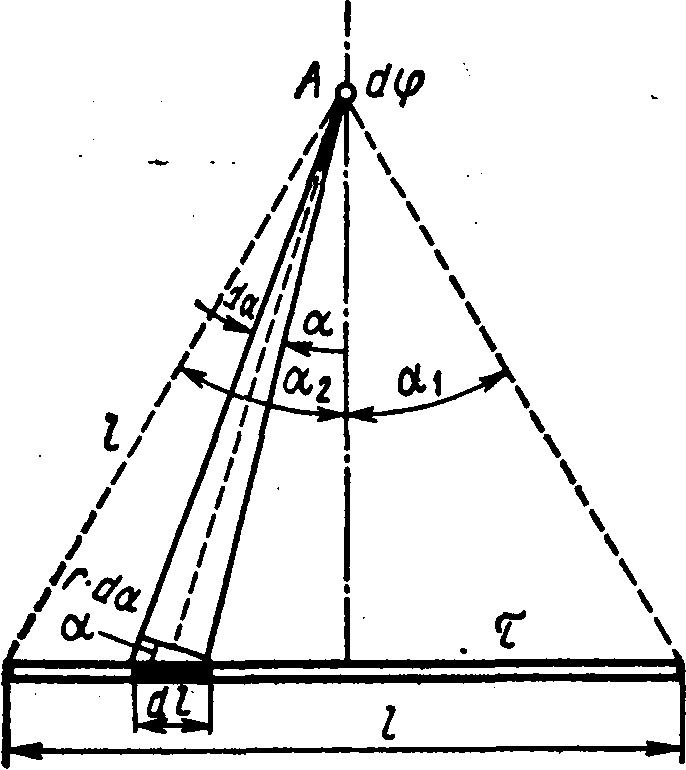 силу симметрии расположения точкиА
относительно концов стержня имеем 2
= 1
и поэтому
силу симметрии расположения точкиА
относительно концов стержня имеем 2
= 1
и поэтому .
.
Следовательно,
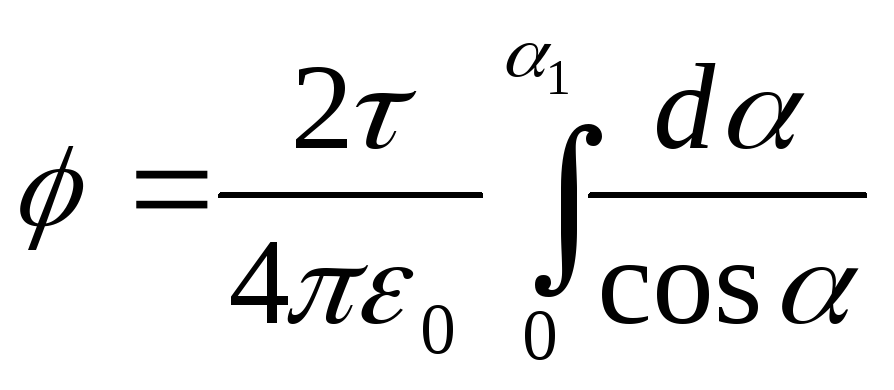 .Так
как
.Так
как
(см. табл. 2), то .
.
Подставляя пределы интегрирования, получим
Сделав вычисления по этой формуле, найдем
Пример 6. Электрон со скоростьюv=1,8310 6 м/с влетел в однородное электрическое поле в направлении, противоположном вектору напряженности поля. Какую разность потенциаловU должен пройти электрон, чтобы обладать энергиейE i =13,6 эВ*? (Обладая такой энергией, электрон при столкновении с атомом водорода может ионизировать его. Энергия 13,6 эВ называется энергией ионизации водорода.)
Решение.
Электрон должен пройти такую разность
потенциаловU,
чтобы приобретенная
при этом энергияW
в
сумме с кинетической энергиейT
,
которой обладал электрон перед вхождением
в поле, составила энергию, равную энергии
ионизацииE
i
,
т. е.W
+
T
=
E
i
.
Выразив в этой формулеW
=
eU
иТ
=(m
v 2
/2),
получимeU
+(m
v 2
/2)=E
i
.
Отсюда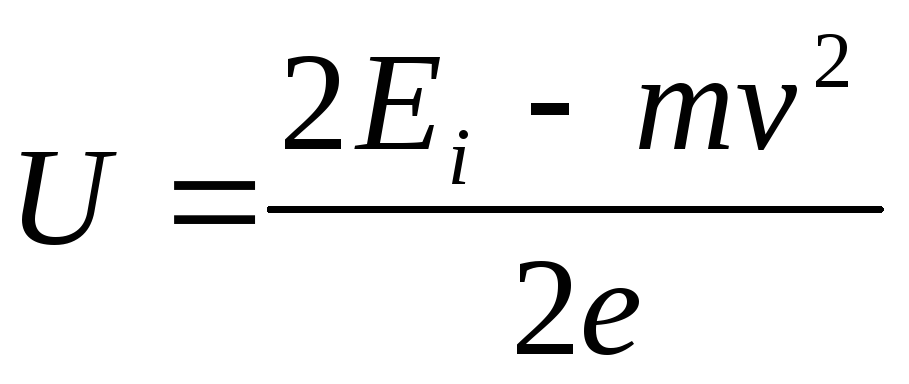 .
.
___________________
* Электрон-вольт (эВ) - энергия, которую приобретает частица, имеющая заряд, равный заряду электрона, прошедшая разность потенциалов 1 В. Эта внесистемная единица энергии в настоящее время допущена к применению в физике.
Произведем вычисления в единицах СИ:
U=4,15 В.
Пример 7. Определить начальную скоростьυ 0 сближения протонов, находящихся на достаточно большом расстоянии друг от друга, если минимальное расстояниеr min , на которое они могут сблизиться, равно 10 -11 см.
Р е ш е н и е. Между двумя протонами действуют силы отталкивания, вследствие чего движение протонов будет замедленным. Поэтому задачу можно решить как в инерциальной системе координат (связанной с центром масс двух протонов), так и в неинерциальной (связанной с одним из ускоренно движущихся протонов). Во втором случае законы Ньютона не имеют места. Применение же принципа Даламбера затруднительно из-за того, что ускорение системы будет переменным. Поэтому удобно рассмотреть задачу в инерциальной системе отсчета.
Поместим начало координат в центр масс двух протонов. Поскольку мы имеем дело с одинаковыми частицами, то центр масс будет находиться в точке, делящей пополам отрезок, соединяющий частицы. Относительно центра масс частицы будут иметь в любой момент времени одинаковые по модулю скорости. Когда частицы находятся на достаточно большом расстоянии друг от друга, скорость υ 1 каждой частицы равна половинеυ 0 , т. е.υ 1 =υ 0 /2.
Для решения задачи применим закон сохранения энергии, согласно которому полная механическая энергия Е изолированной системы постоянна, т. е.
Е=Т+ П,
где Т - сумма кинетических энергий обоих протонов относительно центра масс; П - потенциальная энергия системы зарядов.
Выразим потенциальную энергию в начальный П 1 и конечный П 2 моменты движения.
В начальный момент, согласно условию задачи, протоны находились на большом расстоянии, поэтому потенциальной энергией можно пренебречь (П 1 =0). Следовательно, для начального момента полная энергия будет равна кинетической энергииT 1 протонов, т. е.
E=T l . (1)
В конечный момент, когда протоны максимально сблизятся, скорость и кинетическая энергия равны нулю, а полная энергия будет равна потенциальной энергии П 2 , т. е.
Е= П 2 . (2)
Приравняв правые части равенств (1) и (2), получим
T 1 =П 2 . (3)
Кинетическая энергия равна сумме кинетических энергий протонов:
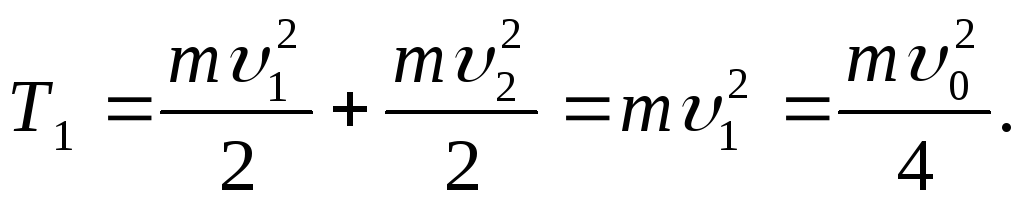 (4)
(4)
Потенциальная
энергия системы двух зарядов Q
1 иQ
2 , находящихся
в вакууме, определяется по формуле ,
гдеr
- расстояние
между зарядами. Воспользовавшись этой
формулой, получим
,
гдеr
- расстояние
между зарядами. Воспользовавшись этой
формулой, получим
 (5)
(5)
С учетом равенств (4) и (5) формула (3) примет вид
 откуда
откуда

Выполнив вычисления по полученной формуле, найдем υ 0 =2,35 Мм/с.
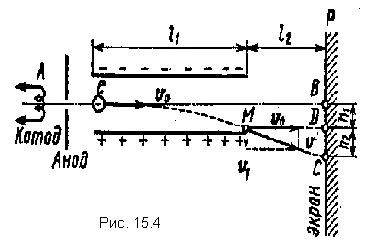 Пример
8.
Электрон без начальной скорости
прошел разность потенциаловU
0 =10
кВ и влетел в пространство между
пластинами плоского конденсатора,
заряженного до разности потенциаловU
l =100 В, по линииАВ,
параллельной пластинам (рис. 15.4).
Расстояниеd
между пластинами
равно 2 см. Длинаl
1 пластин конденсатора в направлении
полета электрона, равна 20cм.
Определить расстояниеВС
на
экранеР,
отстоящем от конденсатора
наl
2 =1 м.
Пример
8.
Электрон без начальной скорости
прошел разность потенциаловU
0 =10
кВ и влетел в пространство между
пластинами плоского конденсатора,
заряженного до разности потенциаловU
l =100 В, по линииАВ,
параллельной пластинам (рис. 15.4).
Расстояниеd
между пластинами
равно 2 см. Длинаl
1 пластин конденсатора в направлении
полета электрона, равна 20cм.
Определить расстояниеВС
на
экранеР,
отстоящем от конденсатора
наl
2 =1 м.
Р е ш е н и е. Движение электрона внутри конденсатора складывается из двух движений: 1) по инерции вдоль линии АВ с постоянной скоростьюυ 0 , приобретенной под действием разности потенциаловU 0 , которую электрон прошел до конденсатора; 2) равномерно ускоренного движения в вертикальном направлении к положительно заряженной пластине под действием постоянной силы поля конденсатора. По выходе из конденсатора электрон будет двигаться равномерно со скоростьюυ, которую он имел в точкеМ в момент вылета из конденсатора.
Из рис. 15.4 видно, что искомое расстояние |BC|=h 1 +h 2 , где сh 1 - расстояние, на которое сместится электрон в вертикальном направлении во время движения в конденсаторе;h 2 - расстояние между точкой D на экране, в которую электрон попал бы, двигаясь по выходе из конденсатора по направлению начальной скоростиυ 0 , и точкой С, в которую электрон попадет в действительности.
Выразим отдельно h 1 иh 2 . Пользуясь формулой длины пути равномерно ускоренного движения, найдем
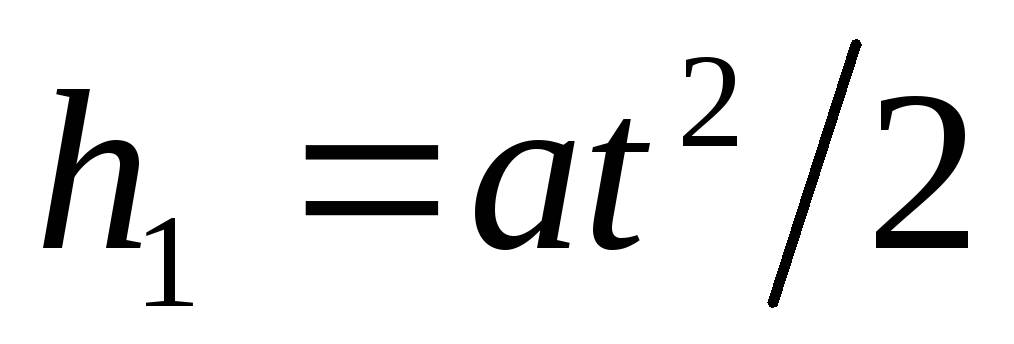 .
(1)
.
(1)
где а - ускорение, полученное электроном под действием поля конденсатора;t- время полета электрона внутри конденсатора.
По второму закону
Ньютона a=F/m,
гдеF
- сила, с которой
поле действует на электрон;т-
его
масса. В свою очередь,F
=eE=eU
1 /d,
гдее
- заряд
электрона;U
1 - разность
потенциалов между пластинами конденсатора;d
- расстояние между ними. Время
полета электрона внутри конденсатора
найдем из формулы пути равномерного
движения
 ,
откуда
,
откуда

где l
1
- длина конденсатора в направлении
полета электрона. Выражение скорости
найдем из условия равенства работы,
совершенной полем при перемещении
электрона, и приобретенной им кинетической
энергии: .
Отсюда
.
Отсюда
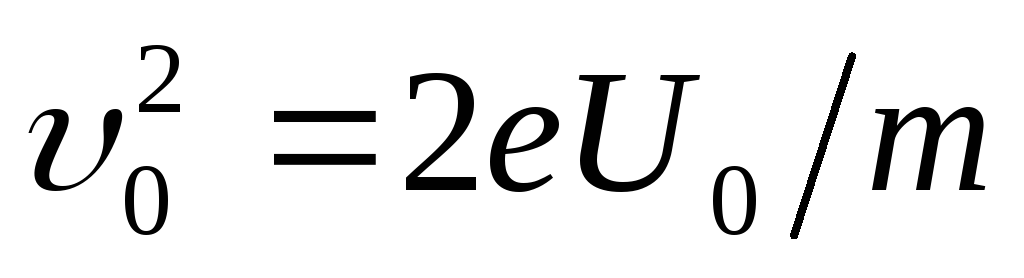 (2)
(2)
Подставляя в
формулу (1) последовательно значения а,
F
, t
иυ
0 2
из соответствующих выражений,
получим
Длину отрезка h 2 найдем из подобия треугольниковMDC и векторного:
 (3)
(3)
где υ 1 - скорость электрона в вертикальном направлении в точкеМ; l 2 - расстояние от конденсатора до экрана.
Скорость υ 1 найдем по формулеυ 1 =at, которая с учетом выражений дляа, F иt примет вид

Подставив выражение
υ
1 в формулу (3), получим ,
или, заменивυ
0 2 по
формуле (3), найдем
,
или, заменивυ
0 2 по
формуле (3), найдем

Окончательно для искомого расстояния |BC | будем иметь
|BC
|=
Подставив значения величин U 1 ,U 0 ,d, l 1 иl 2 в последнее выражение и произведя вычисления, получим |BC |=5,5cм.
Задачи
Потенциальная энергия и потенциал поля точечных зарядов
15.1. Точечный зарядQ = 10 нКл, находясь в некоторой точке поля, обладает потенциальной энергией П = 10 мкДж. Найти потенциал φ этой точки поля.
5.2. При перемещении зарядаQ=20 нКл между двумя точками поля внешними силами была совершена работаА=4 мкДж. Определить работуA 1 сил поля и разность Δφ потенциалов этих точек поля.
15.3. Электрическое поле создано точечным положительным зарядомQ 1 =6 нКл. Положительный зарядQ 2 переносится из точкиА этого поля в точкуВ (рис. 15.5). Каково изменение потенциальной энергии ΔП, приходящееся на единицу переносимого заряда, еслиr 1 =20 см иr 2 =50 см?
15.4.
Электрическое
поле создано точечным зарядомQ
l =50
нКл. Не пользуясь понятием потенциала,
вычислить работуА
в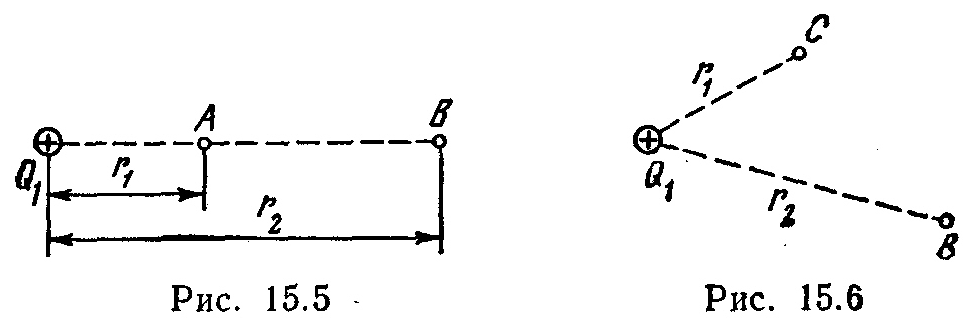 нешних
сил по перемещению точечного зарядаQ
2 = -2 нКл из точкиС
в точкуВ
нешних
сил по перемещению точечного зарядаQ
2 = -2 нКл из точкиС
в точкуВ
(рис. 15.6), если r 1 =10 см,r 2 =20 см. Определить также изменение ΔП потенциальной энергии системы зарядов.
15.5. Поле создано точечным зарядомQ =1 нКл. Определить потенциал φ поля в точке, удаленной от заряда на расстояниеr =20 см.
15.6. Определить потенциал φ электрического поля в точке,удаленной от зарядовQ 1 = -0,2 мкКл иQ 2 =0,5 мкКл соответственно наr 1 =15 см иr 2 =25 см. Определить также минимальное и максимальное расстояния между зарядами, при которых возможно решение.
15.7. ЗарядыQ 1 =1 мкКл иQ 2 = -1 мкКл находятся на расстоянииd =10 см. Определить напряженностьЕ и потенциал φ поля в точке, удаленной на расстояниеr = 10 см от первого заряда и лежащей на линии, проходящей через первый заряд перпендикулярно направлению отQ 1 кQ 2 .
15.8. Вычислить потенциальную энергию П системы двух точечных зарядовQ 1 =100 нКл иQ 2 =10 нКл, находящихся на расстоянииd =10 см друг от друга.
15.9. Найти потенциальную энергию П системы трех точечных зарядовQ 1 =10 нКл,Q 2 =20 нКл иQ 3 = -30 нКл, расположенных в вершинах равностороннего треугольника со стороной длинойa =10 см.
15.10. Какова потенциальная энергия П системы четырех одинаковых точечных зарядовQ =10 нКл, расположенных в вершинах квадрата со стороной длинойа =10 см? .
15.11. Определить потенциальную энергию П системы четырех точечных зарядов, расположенных в вершинах квадрата со стороной длинойa =10 см. Заряды одинаковы по модулюQ =10 нКл,но два из них отрицательны. Рассмотреть два возможных случая расположения зарядов.
 15.12
.
Поле создано двумя точечными зарядами+
2Q
и-Q,
находящимися на
расстоянииd
=12 см друг от друга.
Определить геометрическое место точек
на плоскости, для которых потенциал
равен нулю (написать уравнение линии
нулевого потенциала).
15.12
.
Поле создано двумя точечными зарядами+
2Q
и-Q,
находящимися на
расстоянииd
=12 см друг от друга.
Определить геометрическое место точек
на плоскости, для которых потенциал
равен нулю (написать уравнение линии
нулевого потенциала).
5.13. Система состоит из трех зарядов - двух одинаковых по величинеQ 1 = |Q 2 |=1 мкКл и противоположных по знаку и зарядаQ=20 нКл, расположенного точке 1 посередине между двумя другими зарядами системы (рис. 15.7). Определить изменение потенциальной энергии ΔП системы при переносе зарядаQ из точки 1 в точку 2. Эти точки удалены от отрицательного зарядаQ 1 на расстояниеа= 0,2 м.
Потенциал поля линейно распределенных зарядов
15.14. По тонкому кольцу радиусомR= 10 см равномерно распределен заряд с линейной плотностью τ= 10 нКл/м. Определить потенциал φ в точке, лежащей на оси кольца, на расстоянииа= 5 см от центра.
15.15. На отрезке тонкого прямого проводника равномерно распределен заряд с линейной плотностью τ=10 нКл/м. Вычислить потенциал φ, создаваемый этим зарядом в точке, расположенной на оси проводника и удаленной от ближайшего конца отрезка на расстояние, равное длине этого отрезка.
Лекция 6. Потенциал электрического поля. Контрольная работа № 2
Потенциал относится к самым сложным понятиям электростатики. Учащиеся выучивают определение потенциала электростатического поля, решают многочисленные задачи, но у них нет ощущения потенциала, они с трудом соотносят теорию с реальностью. Поэтому роль учебного эксперимента в формировании понятия потенциала весьма высока. Нужны такие опыты, которые, с одной стороны, иллюстрировали бы абстрактные теоретические представления о потенциале, а с другой, показывали полную обоснованность экспериментом введения понятия потенциала. Стремиться к особой точности количественных результатов в этих опытах скорее вредно, чем полезно.
6.1. Потенциальность электростатического поля
На изолирующей подставке укрепим проводящее тело и зарядим его. На длинной изолированной нити подвесим лёгкий проводящий шарик и сообщим ему пробный заряд, одноимённый с зарядом тела. Шарик оттолкнётся от тела и из положения 1 перейдёт в положение 2. Так как высота шарика в поле тяготения увеличилась на h , потенциальная энергия его взаимодействия с Землёй возросла на mgh. Значит, электрическое поле заряженного тела совершило над пробным зарядом некоторую работу.
Повторим опыт, но в начальный момент не просто отпустим пробный шарик, а толкнём его в произвольном направлении, сообщив ему некоторую кинетическую энергию. При этом обнаружим, что двигаясь из положения 1 по сложной траектории, шарик в конечном итоге остановится в положении 2 . Сообщённая шарику в начальный момент кинетическая энергия, очевидно, израсходовалась на преодоление сил трения при движении шарика, а электрическое поле совершило над шариком ту же работу, что и в первом случае. В самом деле, если уберём заряженное тело, то тот же самый толчок пробного шарика приводит к тому, что из положения 2 он возвращается в положение 1 .
Таким образом, опыт наводит на мысль, что работа электрического поля над зарядом не зависит от траектории движения заряда, а определяется лишь положениями её начальной и конечной точек. Иными словами, на замкнутой траектории работа электростатического поля всегда равна нулю. Поля, обладающие таким свойством, называются потенциальными.
6.2. Потенциальность центрального поля
Опыт показывает, что в электростатическом поле, создаваемом заряженным проводящим шаром, действующая на пробный заряд сила всегда направлена от центра заряженного шара, она монотонно уменьшается с увеличением расстояния и на равных расстояниях от него имеет одинаковые значения. Такое поле называется центральным . Пользуясь рисунком, нетрудно убедиться, что центральное поле потенциально.

6.3. Потенциальная энергия заряда в
электростатическом поле

Гравитационное поле, как и электростатическое, потенциально. Кроме того, математическая запись закона всемирного тяготения совпадает с записью закона Кулона. Поэтому при исследовании электростатического поля имеет смысл опираться на аналогию между гравитационным и электростатическим полями.
В небольшой области вблизи поверхности Земли гравитационное поле можно считать однородным (рис. а ).
На тело массой m в этом поле действует постоянная по модулю и направлению сила f = тg . Если предоставленное самому себе тело падает из положения 1 в положение 2 , то сила тяготения совершает работу A = fs = mgs = mg (h 1 – h 2).
Это же самое мы можем сказать иначе.
Когда тело находилось в положении 1
, система
Земля–тело обладала потенциальной энергией (т.е.
способностью совершить работу) W
1 = mgh
1 .
Когда тело перешло в положение 2
,
рассматриваемая система стала обладать
потенциальной энергией W
2 = mgh
2 .
Совершённая при этом работа равна разности
потенциальных энергий системы в конечном и
начальном состояниях, взятой с обратным знаком: А
= – (W
2 – W
1). 
Обратимся теперь к электрическому полю, которое, напомним, как и гравитационное, является потенциальным. Представим, что силы тяжести нет, а вместо поверхности Земли имеется плоская проводящая пластина, заряженная (для определённости) отрицательно (рис. б ). Введём координатную ось Y и над пластиной расположим положительный заряд q . Понятно, что, поскольку сам по себе заряд не существует, над пластиной находится какое-то тело определённой массы, несущее электрический заряд. Но, поскольку мы считаем поле тяжести отсутствующим, то и принимать во внимание массу заряженного тела не будем.
Итак, на положительный заряд q со стороны отрицательно заряженной плоскости действует сила притяжения f = qE , где E – напряжённость электрического поля. Так как электрическое поле однородно, то во всех его точках на заряд действует одна и та же сила. Если заряд перемещается из положения 1 в положение 2 , то электростатическая сила совершает над ним работу А = fs = qE s = qE (y 1 – y 2).
То же самое мы можем выразить другими словами. В положении 1 находящийся в электростатическом поле заряд обладал потенциальной энергией W 1 = qEy 1 , а в положении 2 – потенциальной энергией W 2 = qEy 2 . При переходе заряда из положения 1 в положение 2 электрическое поле заряженной плоскости совершило над ним работу А = –(W 2 – W 1).
Напомним, что потенциальная энергия определена лишь с точностью до слагаемого: если нулевое значение потенциальной энергии выбрать в другом месте оси Y , то в принципе ничего не изменится.
6.4. Потенциал однородного электростатического поля
Если потенциальную энергию заряда в электростатическом поле разделить на величину этого заряда, то получим энергетическую характеристику самого поля, которую назвали потенциалом :
Потенциал в системе СИ выражают в вольтах : 1 В = 1 Дж/1 Кл.
Если в однородном электрическом поле ось Y направить параллельно вектору напряжённости E , то потенциал произвольной точки поля будет пропорционален координате точки: причём коэффициентом пропорциональности является напряжённость электрического поля.
6.5. Разность потенциалов
Потенциальная энергия и потенциал определяются лишь с точностью до произвольной постоянной, зависящей от выбора их нулевых значений. Однако работа поля имеет вполне определённое значение, поскольку определяется разностью потенциальных энергий в двух точках поля:
А = –(W 2 – W 1) = –( 2 q – 1 q ) = q ( 1 – 2).
Работа по перемещению электрического заряда между двумя точками поля равна произведению заряда на разность потенциалов начальной и конечной точек. Разность потенциалов иначе называют напряжением .
Напряжение между двумя точками равно отношению работы поля при перемещении заряда из начальной точки в конечную к этому заряду:
![]()
Напряжение, как и потенциал, выражается в вольтах.
6.6. Разность потенциалов и напряжённость
В однородном электрическом поле напряжённость направлена в сторону убывания потенциала и, согласно формуле = Еy , разность потенциалов равна U = 1 – 2 = Е (у 1 – y 2). Обозначив разность координат точек у 1 – y 2 = d , получаем U = Ed .
В эксперименте вместо непосредственного измерения напряжённости проще определять разность потенциалов и затем вычислять модуль напряжённости по формуле
где d – расстояние между двумя точками поля, близко расположенными в направлении вектора Е . При этом в качестве единицы напряжённости используют не ньютон на кулон, а вольт на метр:
![]()
6.7. Потенциал произвольного электростатического поля
Опыт показывает, что отношение работы по перемещению заряда из бесконечности в данную точку поля к величине этого заряда остаётся неизменным: = А /q . Это отношение принято называть потенциалом данной точки электростатического поля , принимая потенциал в бесконечности равным нулю.
6.8. Принцип суперпозиции для потенциалов
Любое как угодно сложное электростатическое поле можно представить в виде суперпозиции полей точечных зарядов. Каждое такое поле в выбранной точке имеет определённый потенциал. Поскольку потенциал является скалярной величиной, результирующий потенциал поля всех точечных зарядов есть алгебраическая сумма потенциалов 1 , 2 , 3 , … полей отдельных зарядов: = 1 + 2 + 3 + ... Это соотношение является прямым следствием принципа суперпозиции электрических полей.
6.9. Потенциал поля точечного заряда
Обратимся теперь к сферическому
(точечному) заряду. Выше показано, что
напряжённость электрического поля, созданного
равномерно распределённым по сфере зарядом Q
,
не зависит от радиуса сферы. Представим, что на
некотором расстоянии r
от центра сферы
находится пробный заряд q
. Напряжённость
поля в точке, где находится заряд, 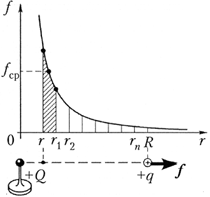
На рисунке изображён график
зависимости силы электростатического
взаимодействия между точечными зарядами от
расстояния между ними. Чтобы найти работу
электрического поля при перемещении пробного
заряда q
с расстояния r
до расстояния R
,
разобьём этот промежуток точками r
1 , r
2 ,...,
r п
на равные отрезки. Средняя сила,
действующая на заряд q
в пределах отрезка [rr
1 ],
равна ![]()
Работа этой силы на этом участке:
![]()
Аналогичные выражения для работы получатся для всех других участков. Поэтому полная работа:
Одинаковые слагаемые с противоположными знаками уничтожаются, и окончательно получаем:
– работа поля над зарядом ![]()
– разность потенциалов ![]()
Теперь, чтобы найти потенциал точки поля относительно бесконечности, устремляем R к бесконечности и окончательно получаем:
Итак, потенциал поля точечного заряда обратно пропорционален расстоянию до заряда.
6.10. Эквипотенциальные поверхности
Поверхность, в каждой точке которой потенциал электрического поля имеет одно и то же значение, называется эквипотенциальной. Эквипотенциальные поверхности поля заряженного шара нетрудно продемонстрировать подвешенным на нити пробным зарядом, как это показано на рисунке.
На втором рисунке электростатическое поле двух разноимённых зарядов представлено силовыми (сплошные) и эквипотенциальными (пунктирные) линиями.
Исследование 6.1. Разность
потенциалов
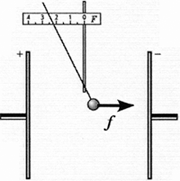
Задание . Разработайте простой опыт, позволяющий ввести понятие разности потенциалов, или напряжения.
Вариант выполнения. Два металлических диска на изолирующих подставках установите параллельно друг другу на расстоянии примерно 10 см. Диски зарядите равными по модулю и противоположными по знаку зарядами. Зарядите шарик электростатического динамометра зарядом, например, q = 5 нКл (см. исследование 3.6), и введите его в область между дисками. При этом стрелка динамометра покажет определённое значение силы, действующей на шарик. Зная параметры динамометра, вычислите значение модуля силы (см. исследование 3.6). Например, в одном из наших опытов стрелка динамометра показала значение х = 2 см, следовательно, согласно формуле модуль силы f = Kх = 17 10 –5 Н.
Перемещая динамометр, покажите, что во всех точках поля между заряженными дисками на пробный заряд действует одна и та же сила. Перемещая динамометр так, чтобы пробный заряд прошёл путь s = 5 см в направлении действующей на него силы, спросите учащихся: какую работу совершает над зарядом электрическое поле? Добейтесь понимания, что работа поля над зарядом по модулю равна
А = fs = 8,5 10 –6 Дж, (6.3)
причём она положительна, если заряд перемещается по направлению напряжённости поля, и отрицательна, если в противоположном направлении. Вычислите разность потенциалов между начальным и конечным положениями шарика динамометра: U = А /q = 1,7 10 3 В.
С одной стороны напряжённость электрического поля между пластинами:
![]()
С другой стороны, согласно формуле (6.1), при d = s :
![]()
Таким образом, опыт показывает, что напряжённость электрического поля можно определить двумя способами, которые, разумеется, приводят к одинаковым результатам.
Исследование 6.2. Градуировка
электрометра по напряжению

Задание. Разработайте эксперимент, показывающий, что с помощью демонстрационного стрелочного электрометра можно измерять напряжение.
Вариант выполнения. Экспериментальная установка схематически изображена на рисунке. Пользуясь электростатическим динамометром, определите напряжённость однородного электрического поля и по формуле U = Еd вычислите разность потенциалов между проводящими пластинами. Повторяя эти действия, отградуируйте электрометр по напряжению так, чтобы получился электростатический вольтметр.
Исследование 6.3. Потенциал поля сферического заряда
Задание. Экспериментально определите работу, которую нужно совершить против электростатического поля, чтобы переместить пробный заряд из бесконечности в некоторую точку поля, созданного заряженной сферой.
Вариант выполнения. На изолирующей стойке закрепите шарик из пенопласта, обёрнутый алюминиевой фольгой. Зарядите его от пьезоэлектрического или иного источника (cм. п. 1.10) и одноимённым зарядом зарядите пробный шарик на стержне электростатического динамометра. Пробный заряд находится бесконечно далеко от исследуемого, если электростатический динамометр не фиксирует силы электростатического взаимодействия между зарядами. В эксперименте удобно электростатический динамометр оставить неподвижным, а перемещать исследуемый заряд.
Постепенно приближайте заряженный шарик на изолирующей подставке к шарику электростатического динамометра. В первую строку таблицы записывайте значения расстояния r между зарядами, во вторую строку – соответствующие им значения силы электростатического взаимодействия. Удобно расстояние выражать в сантиметрах, а силу – в условных единицах, в которых отградуирована шкала динамометра. По получившимся данным постройте график зависимости силы от расстояния. Подобный график вы уже строили, выполняя исследование 3.5.
Теперь найдите зависимость работы по перемещению заряда из бесконечности в данную точку поля. Обратите внимание на то, что в эксперименте сила взаимодействия зарядов становится практически равной нулю на сравнительно небольшом удалении одного заряда от другого.
Разбейте весь диапазон изменения расстояния между зарядами на равные участки, например, по 1 см. Обработку экспериментальных данных удобнее начинать с конца графика. На участке от 16 до 12 см среднее значение силы f ср составляет 0,13 усл. ед., поэтому элементарная работа А на этом участке равна 0,52 усл. ед. На участке от 12 до 10 см, рассуждая аналогичным образом, получаем элементарную работу 0,56 усл. ед. Далее удобно брать участки длиной по 1 см. На каждом из них найдите среднее значение силы и умножьте его на длину участка. Полученные значения работы поля A на всех участках занесите в четвёртую строку таблицы.
Чтобы узнать работу А , совершённую электрическим полем при перемещении заряда из бесконечности на данное расстояние, складывайте соответствующие элементарные работы и получающиеся значения записывайте в пятую строку таблицы. В последней строке запишите значения величины 1/r , обратной расстоянию между зарядами.
Постройте график зависимости работы электрического поля от величины, обратной расстоянию, и убедитесь, что получается прямая линия (рисунок справа).
Таким образом, опыт показывает, что работа электрического поля при перемещении заряда из бесконечности в данную точку поля обратно пропорциональна расстоянию от этой точки до заряда, создающего поле.
Исследование 6.4. Высоковольтный источник напряжения
Информация. Для школьного физического эксперимента в настоящее время промышленность выпускает прекрасные высоковольтные источники напряжения. Они имеют две выходные клеммы или два высоковольтных электрода, разность потенциалов между которыми плавно регулируется в пределах от 0 до 25 кВ. Встроенный в прибор стрелочный или цифровой измеритель напряжения позволяет определять разность потенциалов между полюсами источника. Такие приборы повышают уровень учебного эксперимента по электростатике.
Задание. Разработайте доказательный учебный эксперимент, показывающий, что потенциал заряженного шара, экспериментально определённый в соответствии с формулой (6.2) для точечного заряда, равен потенциалу, сообщённому этому шару высоковольтным источником питания.
Вариант выполнения. Вновь соберите экспериментальную установку, состоящую из электростатического динамометра с пробным шариком и проводящего шара на изолирующей подставке (см. исследования 3.4 и 6.3). Измерьте параметры всех элементов установки.
Для определённости укажем, что в одном
из опытов мы использовали электростатический
динамометр, параметры которого указаны в
исследовании 3.4: а
= 5 10 –3 м, b
= 55
10 –3 м, с
= 100 10 –3 м, т
= 0,94
10 –3 кг, причём шарики были одинаковыми и
имели радиус R
= 7,5 10 –3 м.
Для этого динамометра градуировочный
коэффициент K
, переводящий условные единицы
силы в ньютоны, даётся формулой ![]() (cм. исследование 3.6).
(cм. исследование 3.6).
График работы по перемещению пробного
заряда из бесконечности в данную точку поля
представлен на рисунке на с. 31. Чтобы в этом
графике от условных единиц работы перейти к
джоулям, нужно в соответствии с формулой A
= f
ср r
значения
расстояния в сантиметрах перевести в метры,
значения силы в усл. ед. (см) перевести в усл. ед. (м)
и умножить на K
. Таким образом: A
(Дж) = 10 –4 K
A
(уcл. ед.). 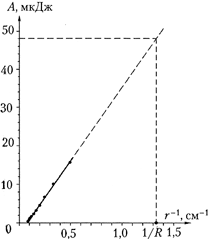
Соответствующий график зависимости работы от величины, обратной расстоянию, представлен ниже. Экстраполируя его до R = 7,5 мм, получаем, что работа по перемещению пробного заряда из бесконечности до поверхности заряженного шарика А = 57 10 –4 K = 4,8 10 –5 Дж. Так как заряды шариков были одинаковы и составляли q = 6,6 10 –9 Кл (см. исследование 3.6), то искомый потенциал = А /q = 7300 В.

Включите высоковольтный источник и регулятором установите на нём выходное напряжение, например, U = 15 кВ. Одним из электродов поочерёдно прикоснитесь к проводящим шарикам и выключите источник. При этом каждый из шариков приобретает относительно Земли потенциал = 7,5 кВ. Повторите опыт по определению зарядов шариков методом Кулона (исследование 3.6) и вы получите значение, близкое к 7 нКл.
Таким образом, в эксперименте двумя независимыми способами определены заряды шаров. Первый способ основан на непосредственном использовании определения потенциала, второй опирается на сообщение шарикам определённого потенциала c помощью высоковольтного источника и последующее измерение их заряда с помощью закона Кулона. При этом получились совпадающие результаты.
Конечно, никто из школьников и не сомневается в том, что современные приборы правильно измеряют значения физических величин. Но теперь они убеждены, что правильно измеряются именно те величины, которые они изучают в простейших явлениях. Установлена прочная связь между основами физики и современной техникой, ликвидирована пропасть между школьными знаниями и реальной жизнью.
Вопросы и задания для самоконтроля
1. Как экспериментально доказать, что электростатическое поле потенциально?
2. В чём суть аналогии между гравитационным и электростатическим полями?
3. Какова связь между напряжённостью и разностью потенциалов электростатического поля?
4. Предложите опыт, непосредственно обосновывающий справедливость принципа суперпозиции для потенциалов.
5. Вычислите потенциал поля точечного заряда, пользуясь интегральным исчислением. Сравните сделанный вами вывод формулы с элементарным выводом, приведённым в лекции.
6. Выясните, почему в опыте по определению разности потенциалов между двумя проводящими дисками (исследование 6.1) нельзя перемещать измеритель напряжённости так, чтобы его пробный шарик прошёл всё расстояние от одного диска до другого.
7. Отградуировав электрометр по напряжению (исследование 6.2), сравните получившийся результат с теми значениями чувствительности прибора по напряжению, которые приводятся в паспортных данных электрометра.
9. Детально разработайте методику формирования в сознании учащихся обоснованной убеждённости, что введённое при изучении электростатики понятие потенциала электрического поля в точности соответствует тому, которое используется современной наукой и техникой.
Литература
Бутиков Е.И. , Кондратьев А.С. Физика: Учеб. пособие: В 3 кн. Кн. 2. Электродинамика. Оптика. – М.: Физматлит, 2004.
Восканян А.Г ., Марленский А.Д. , Шибаев А.Ф. Демонстрация закона Кулона на основе количественных измерений: В сб. «Учебный эксперимент по электродинамике», вып. 7. – М.: Школа-Пресс, 1996.
Касьянов В.А. Физика-10. – М.: Дрофа, 2003.
Мякишев Г.Я. , Синяков А.З ., Слободсков Б.А . Физика: Электродинамика. 10–11 кл.: Учеб. для угл. изучения физики. – М.: Дрофа, 2002.
Учебное оборудование для кабинетов физики обще- образовательных учреждений: Под ред. Г.Г.Никифорова. – М.: Дрофа, 2005.
Тема 3. ПОТЕНЦИАЛ И РАБОТА ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ. СВЯЗЬ НАПРЯЖЕННОСТИ С ПОТЕНЦИАЛОМ
3.4. Диполь в электрическом поле
3.5. Связь между напряженностью и потенциалом электростатического поля
3.6. Силовые линии и эквипотенциальные поверхности
3.7. Вычисление разности потенциалов по напряженности поля простейших электростатических полей
3.1. Работа сил электростатического поля
Сила, действующая на точечный заряд, находящийся в поле другого неподвижного точечного заряда, является центральной. Направление силы, действующей в любой точке пространства на заряд, проходит через центр заряда, создающего поле, а значение силы зависит только от расстояния до этого заряда до точки наблюдения. (Например, поле силы тяжести является полем центральных сил).
до точки наблюдения. (Например, поле силы тяжести является полем центральных сил).Е
Рис. 3,1
сли тело поставлено в такие условия, что в каждой точке пространства оно подвержено воздействию других тел с силой, закономерно изменяющейся от точки к точке, то говорят, что это тело находится в поле сил. Центральное поле сил потенциально. Убедимся, что электрическое поле потенциально. Вычислим работу, которая совершается силами поля неподвижного точечного заряда q
над перемещающимся в этом поле точечным зарядом  (рис. 3.1). Работа на элементарном пути
(рис. 3.1). Работа на элементарном пути 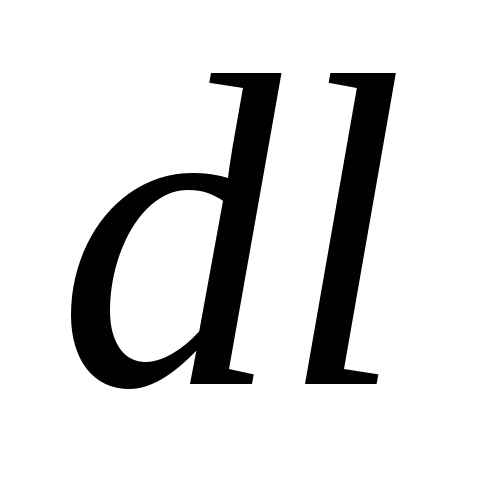 равна:
равна: 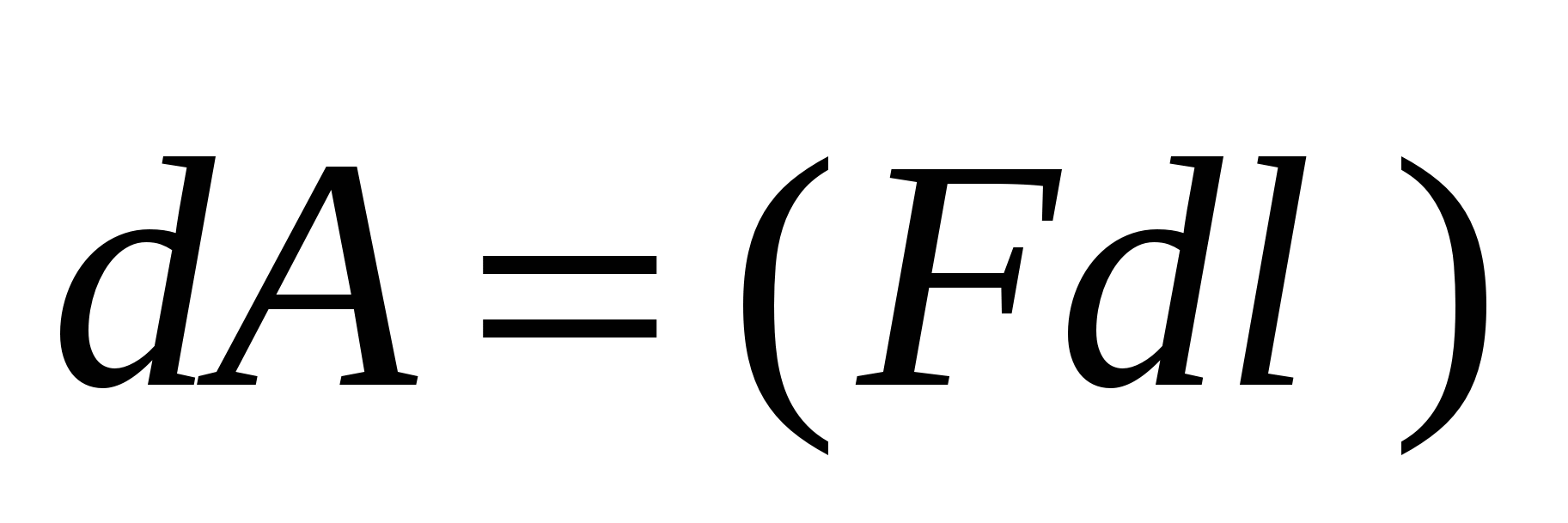 или
или
Так как  . Отсюда на пути 1–2
. Отсюда на пути 1–2
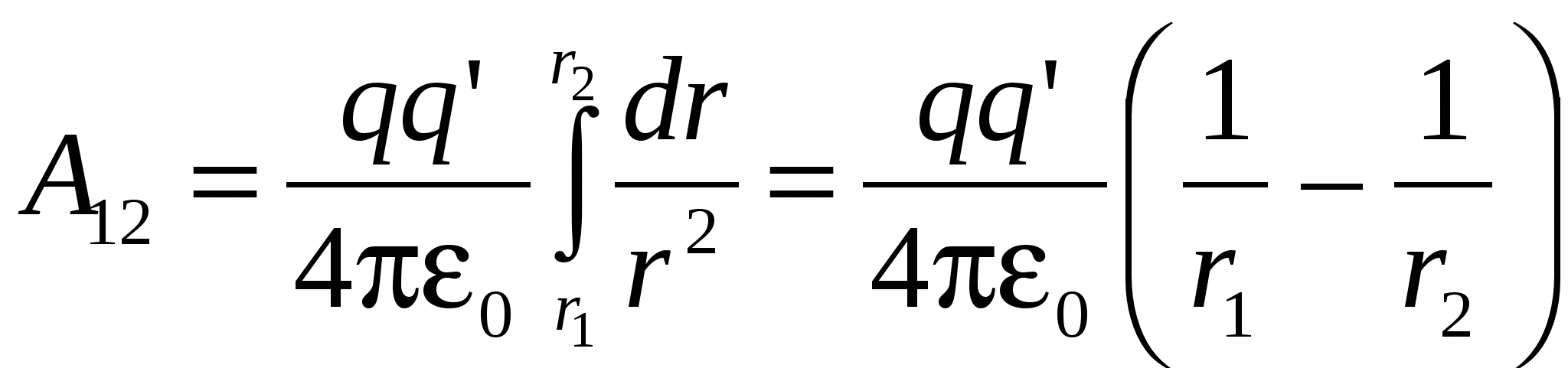 (1)
(1)
Видно, что работа не зависит от пути, по которому перемещался в электрическом поле заряд q
"
, а зависит лишь от начального и конечного положений этого заряда (от r
1 и r
2). Следовательно, силы, действующие на заряд q
"
в поле неподвижного заряда q
, являются консервативными, а поле этих сил потенциальным
. Этот вывод легко распространяется на поле любой системы неподвижных зарядов, так как сила  , действующая на точечный заряд q
" в таком поле, может по принципу суперпозиции быть представлена в виде
, действующая на точечный заряд q
" в таком поле, может по принципу суперпозиции быть представлена в виде  , где
, где  – сила, обусловленная i
-м зарядом создающей поле системы. Работа в этом случае равна алгебраической сумме работ, совершаемых отдельными силами:
– сила, обусловленная i
-м зарядом создающей поле системы. Работа в этом случае равна алгебраической сумме работ, совершаемых отдельными силами:  . Каждое из слагаемых в правой части этого выражения не зависит от пути. Поэтому не зависит от пути и работа А
.
. Каждое из слагаемых в правой части этого выражения не зависит от пути. Поэтому не зависит от пути и работа А
.
Из механики известно, что работа потенциальных сил на замкнутом пути равна нулю. Работа, совершаемая силами поля над зарядом q
"
при обходе по замкнутому контуру, может быть представлена как  , где
, где  –проекция вектора
–проекция вектора  на направление элементарного перемещения , то, следовательно:
на направление элементарного перемещения , то, следовательно:
 (2)
(2)
Это соотношение должно выполняться для любого замкнутого контура. Следует иметь в виду, что (21) справедливо только для электростатического поля. Поле движущихся зарядов (т.е. поле, изменяющееся со временем) не является потенциальным. Следовательно, условие (21) для него не выполняется.
Выражение вида  называется циркуляцией вектора
называется циркуляцией вектора  по данному контуру. Таким образом, характерным для электростатического поля является то, что циркуляция вектора напряженности по любому замкнутому контуру равна нулю.
по данному контуру. Таким образом, характерным для электростатического поля является то, что циркуляция вектора напряженности по любому замкнутому контуру равна нулю.
3.2. Теорема о циркуляции вектора напряженности электростатического поля
Итак, мы утверждаем, что циркуляция вектора  в любом электростатическом поле равна нулю, т.е. . Это утверждение называют теоремой о циркуляции вектора .
в любом электростатическом поле равна нулю, т.е. . Это утверждение называют теоремой о циркуляции вектора .
Пусть в заданном поле с напряженностью перемещается заряд по замкнутому пути 1а2б1. Для доказательства теоремы разобьем произвольный замкнутый путь на две части 1а2 и 2б1 (см. рисунок). Найдем работу по перемещению заряда q
из точки 1 в точку 2. Так как работа в заданном поле не зависит от формы пути, то работа по перемещению заряда по пути 1а2 равна работе по перемещению заряда по пути 1б2 или 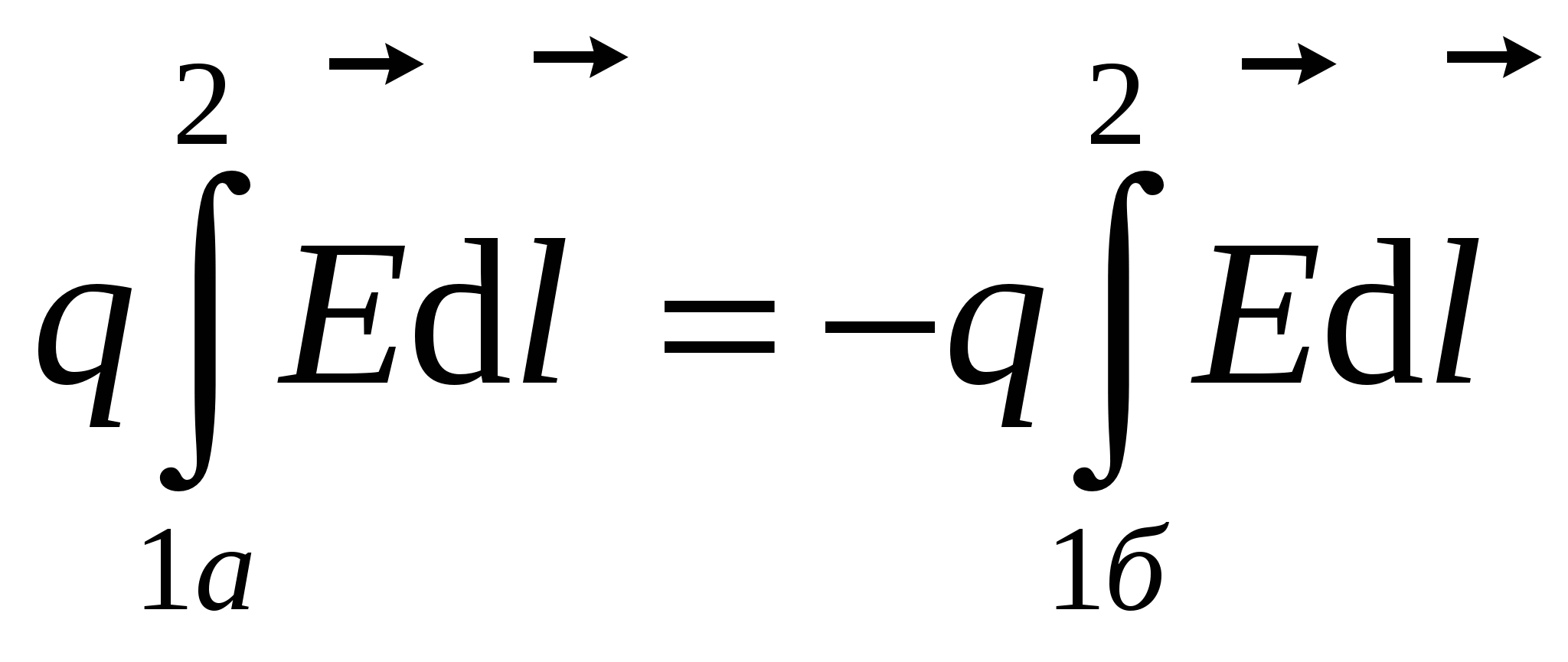

Рисунок 3.2
Из сказанного выше следует, что

(Интегралы по модулю равны, но знаки противоположны). Тогда работа по замкнутому пути:
 (3)
(3)
или 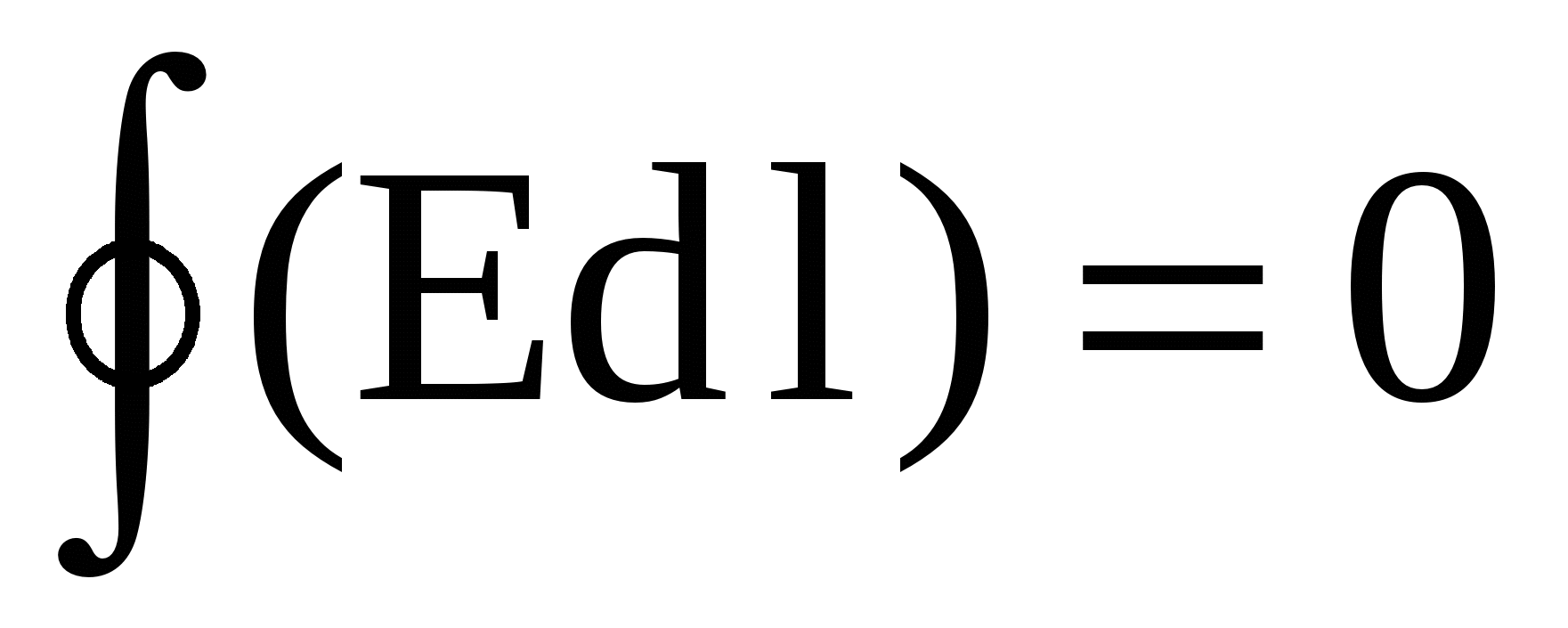 (4)
(4)
Поле, обладающее такими свойствами, называется потенциальным . Любое электростатическое поле является потенциальным.
Теорема о циркуляции позволяет сделать ряд важных выводов, практически не прибегая к расчетам. Рассмотрим два простых примера, подтверждающих это заключение.
Воспользуемся теоремой Стокса, которая гласит, что циркуляция вектора  по произвольному контуру L
равна потоку ротора этого вектора через любую поверхность, натянутую на этот контур, т.е.
по произвольному контуру L
равна потоку ротора этого вектора через любую поверхность, натянутую на этот контур, т.е.  . В случае электростатического поля имеем
. В случае электростатического поля имеем 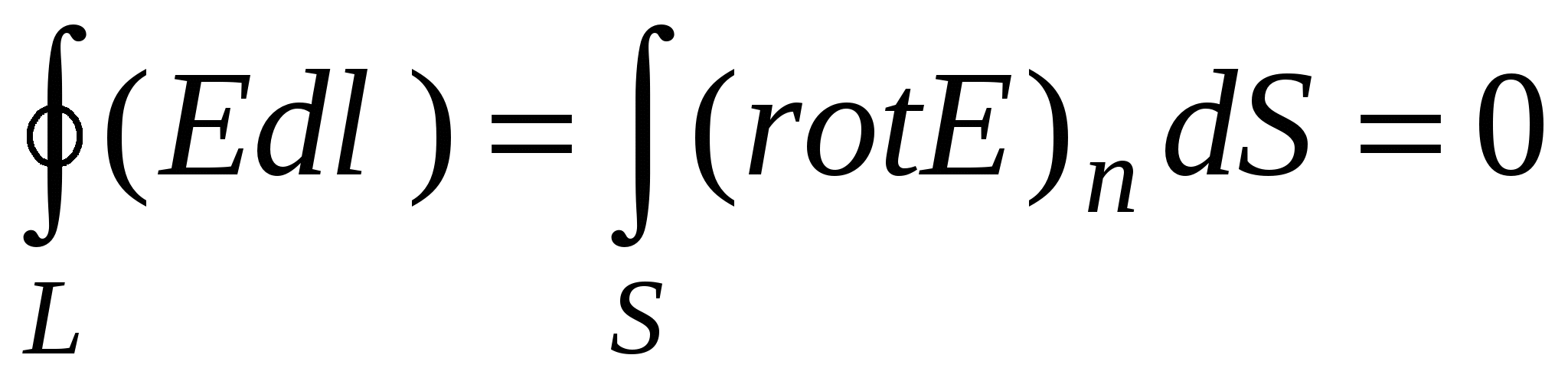 , поэтому в силу произвольности вида поверхности получим
, поэтому в силу произвольности вида поверхности получим 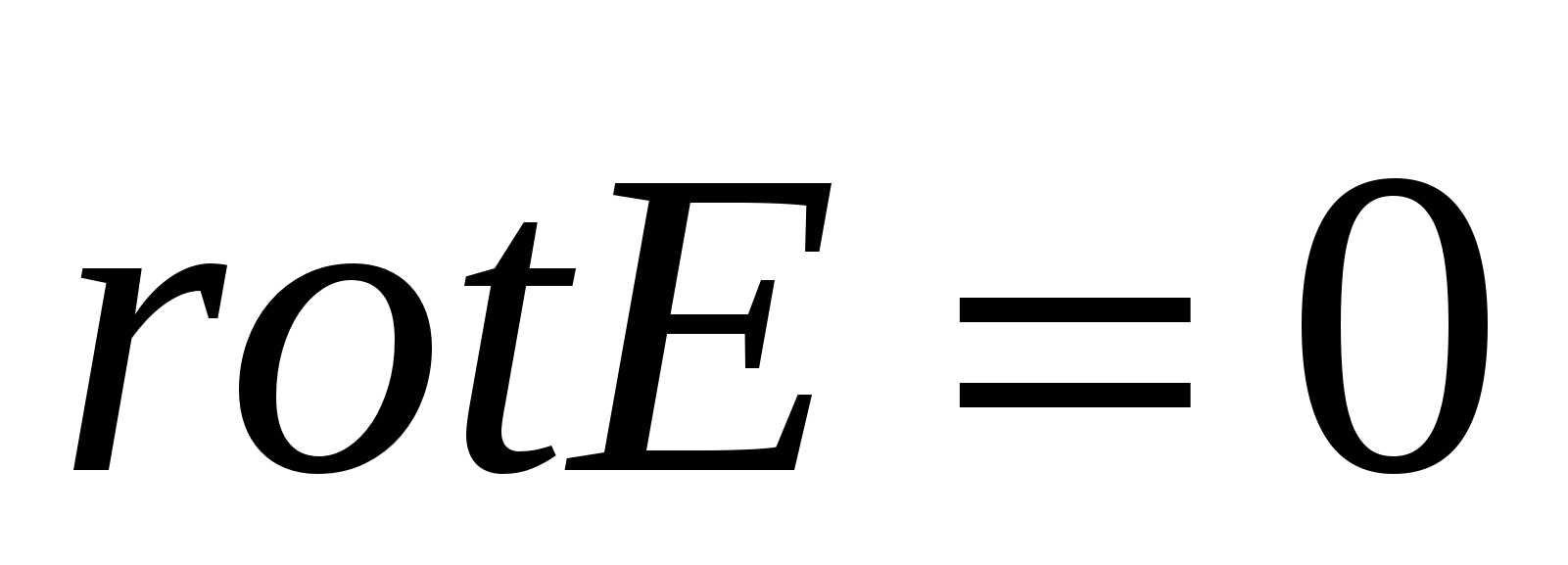 . Следовательно, из потенциального характера электростатического поля вытекает, что электростатическое поле не вихревое, если
.
(5)
. Следовательно, из потенциального характера электростатического поля вытекает, что электростатическое поле не вихревое, если
.
(5)
3.3. Потенциальная энергия и потенциал электростатического поля
Тело, находящееся в поле потенциальных сил, обладает потенциальной энергией, за счет которой совершается работа силами поля. Следовательно, работа может быть представлена как разность значений потенциальных энергий, которыми обладает заряд q " в точках 1 и 2 поля заряда q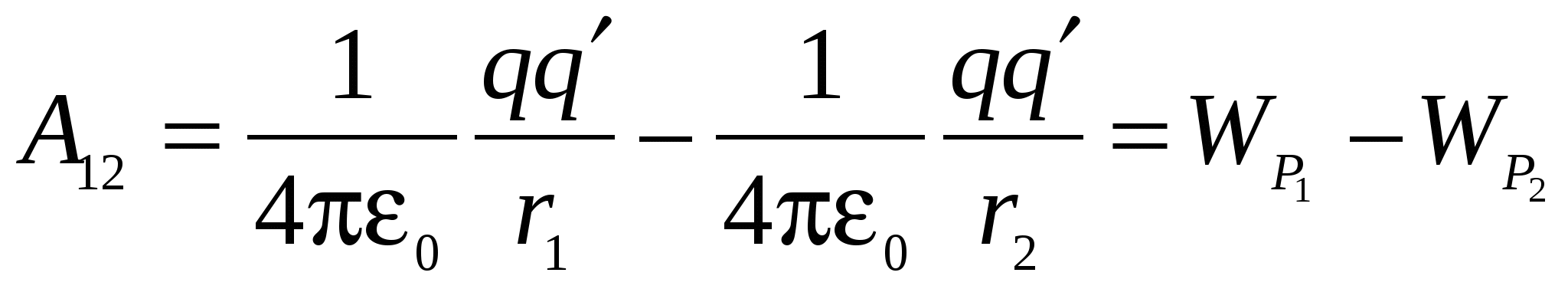
Можно показать также, что, так как 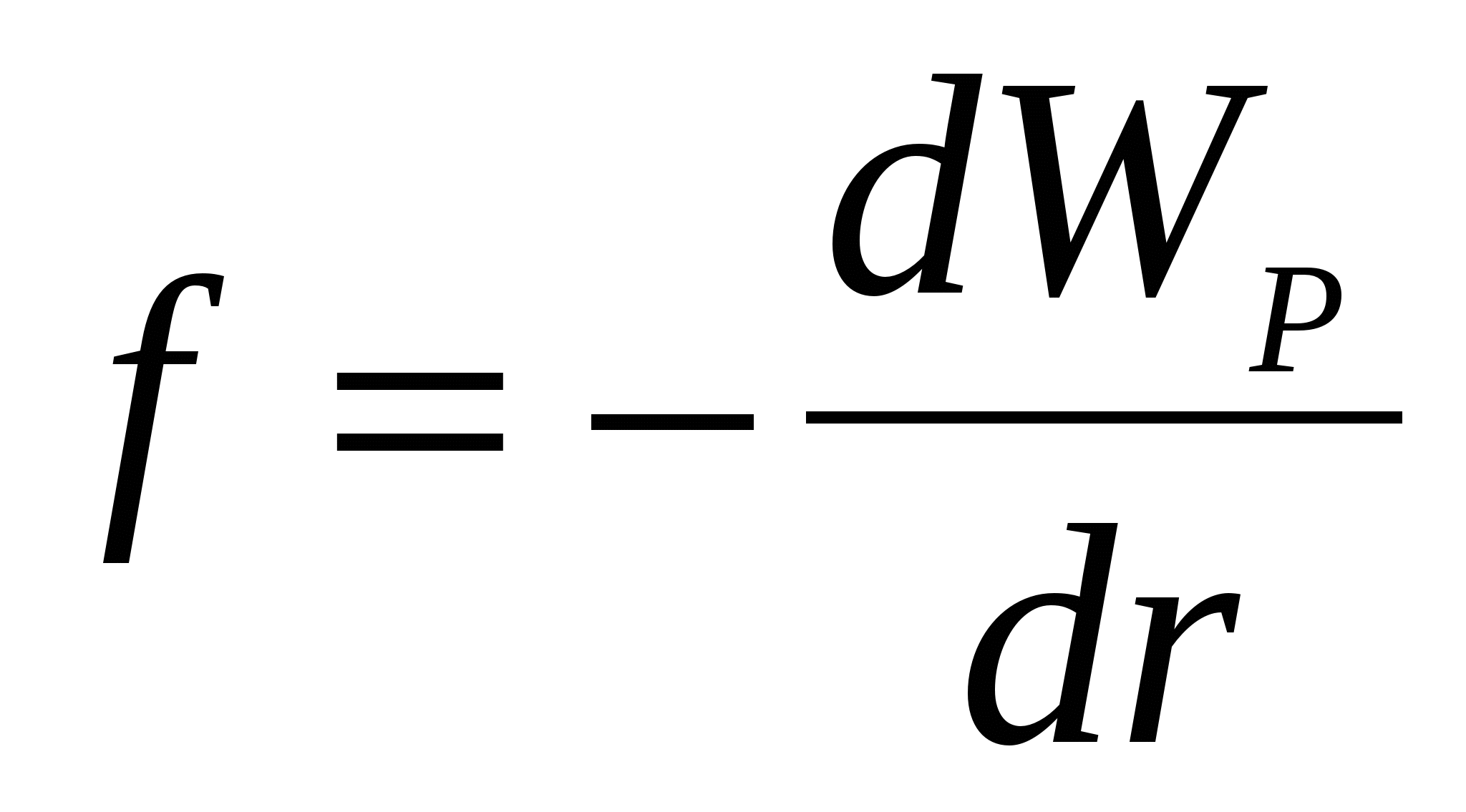 ,
, 
![]() .
.
Отсюда для потенциальной энергии заряда в поле заряда q получаем:
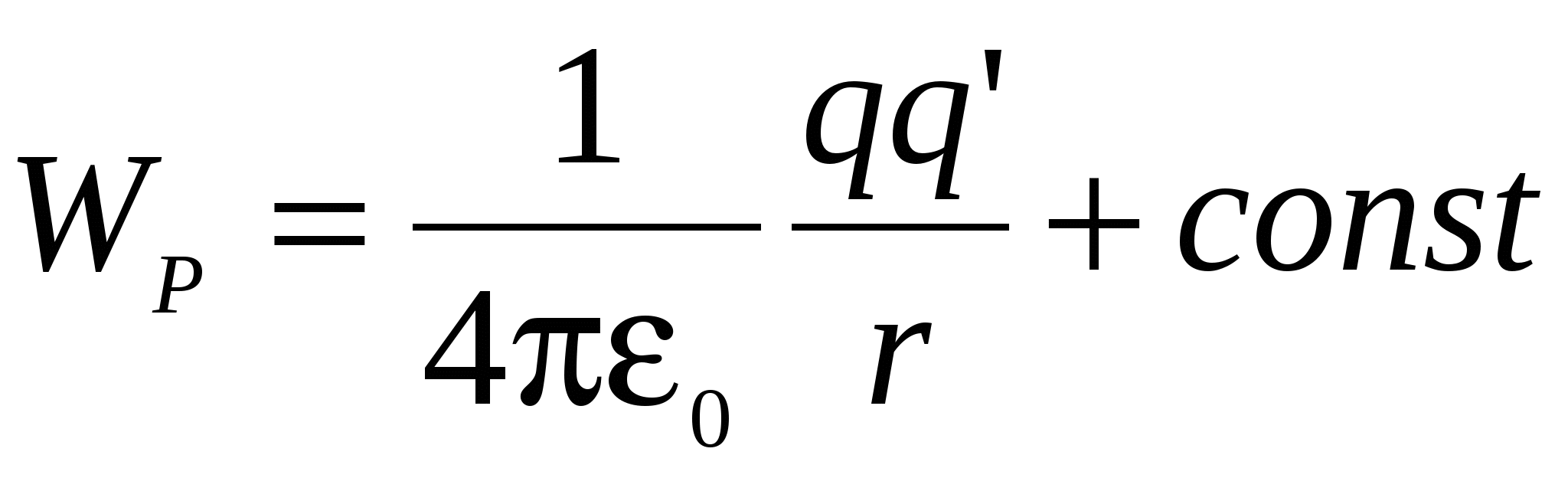 (6)
(6)
Значение const
в (6) обычно выбирают таким образом, чтобы при удалении заряда q
"
на бесконечность ( ) потенциальная энергия обращалась в нуль. При этом условии получается, что
) потенциальная энергия обращалась в нуль. При этом условии получается, что
 (7)
(7)
Будем считать q
"
пробным зарядом. Тогда потенциальная энергия, которой обладает пробный заряд, зависит не только от его значения 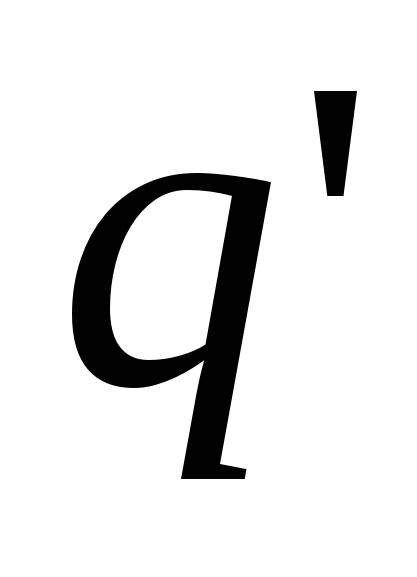 , но и от значения q
и r
, определяющих поле. Следовательно, эта энергия может быть использована для описания поля, подобно тому, как была использована для этой цели сила, действующая на пробный заряд.
, но и от значения q
и r
, определяющих поле. Следовательно, эта энергия может быть использована для описания поля, подобно тому, как была использована для этой цели сила, действующая на пробный заряд.
Разные пробные заряды  ,
, 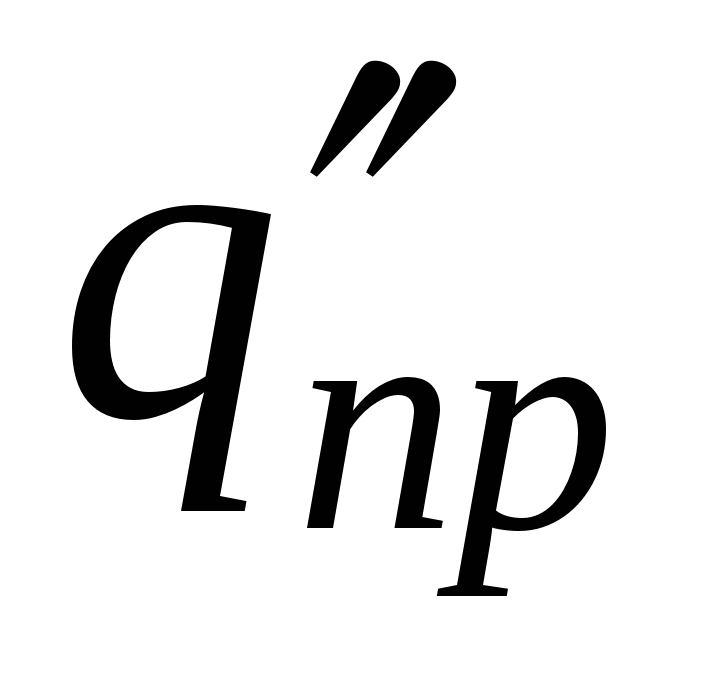 будут обладать в одной и той же точке поля различной энергией
будут обладать в одной и той же точке поля различной энергией  ,
, 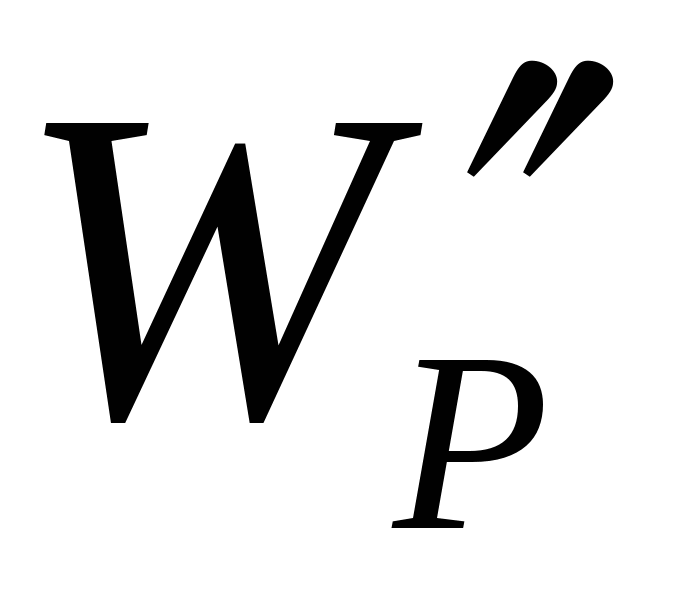 и т.д. Однако отношение
и т.д. Однако отношение 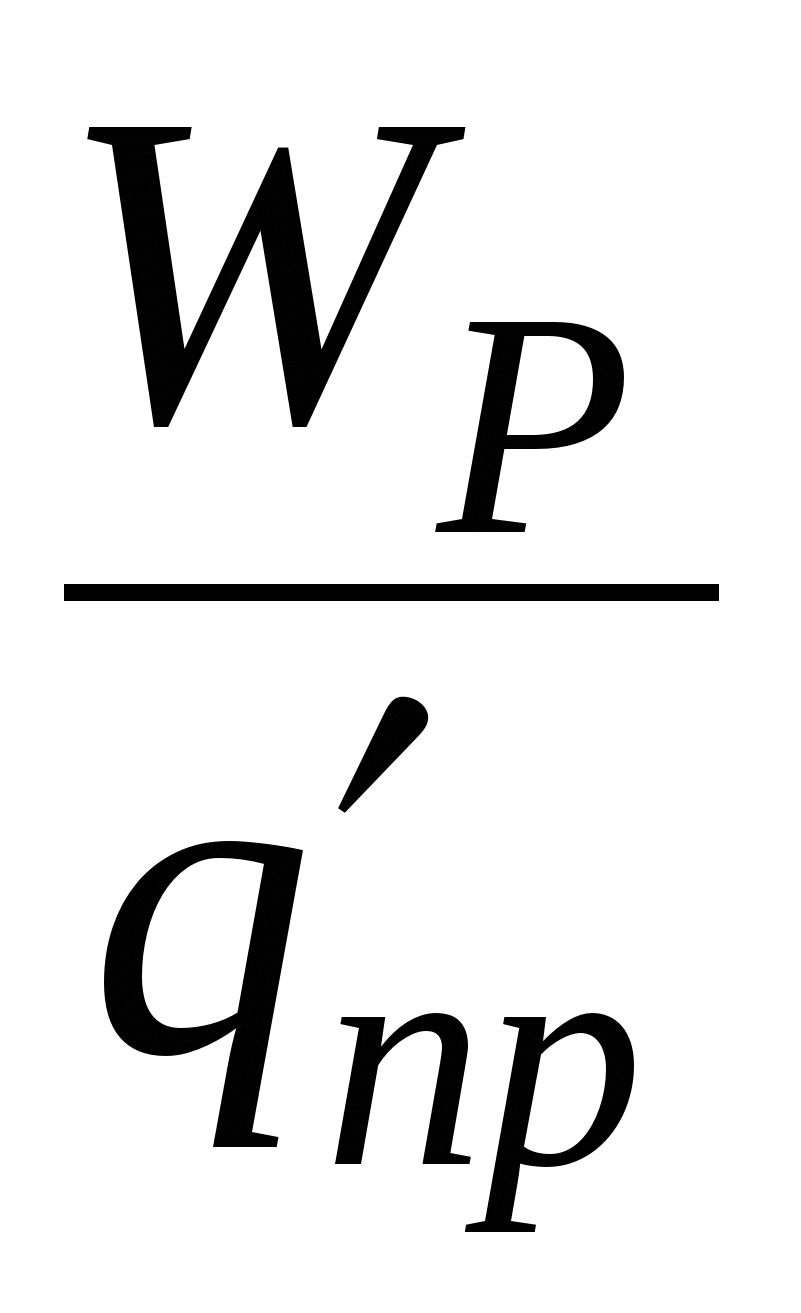 будет для всех зарядов одно и то же. Величина
будет для всех зарядов одно и то же. Величина
 (8)
(8)
Называется потенциалом поля в данной точке и используется наряду с напряженностью поля , для описания электрических полей.
Как следует из (8) потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд.
Таким образом, для потенциального поля точечного заряда получаем следующее выражение:
 (9)
(9)
Если поле создано системой точечных зарядов q
1
, q
2
, …, q
n
, находящихся на расстояниях соответственно r
1
, r
2
,…, r
n
до точки поля, в которой находится заряд  , то работа, совершаемая силами этого поля над зарядом
, то работа, совершаемая силами этого поля над зарядом  , будет равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности:
, будет равна алгебраической сумме работ сил, обусловленных каждым из зарядов в отдельности:
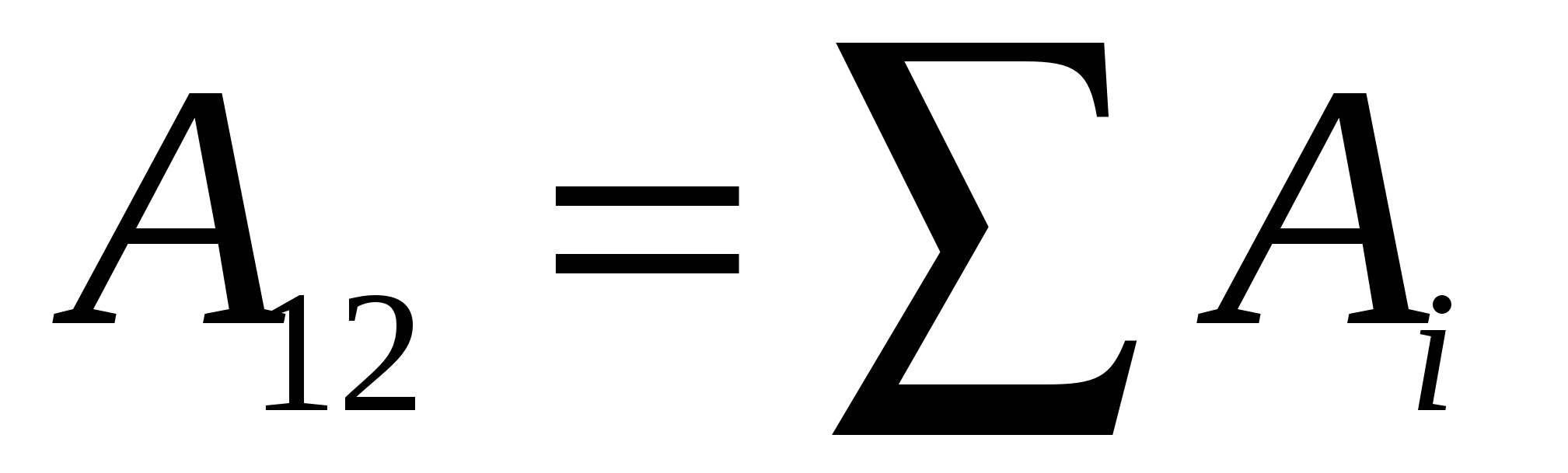 .
.
Но каждая из работ  равна:
равна:
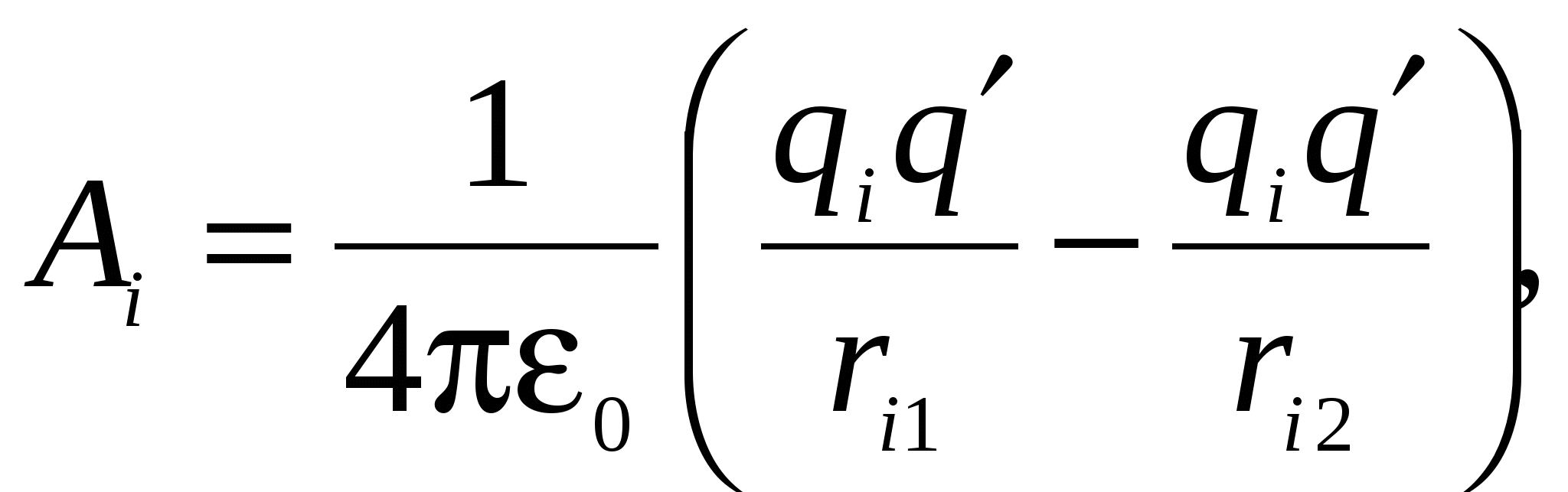
Где  расстояние от заряда
расстояние от заряда 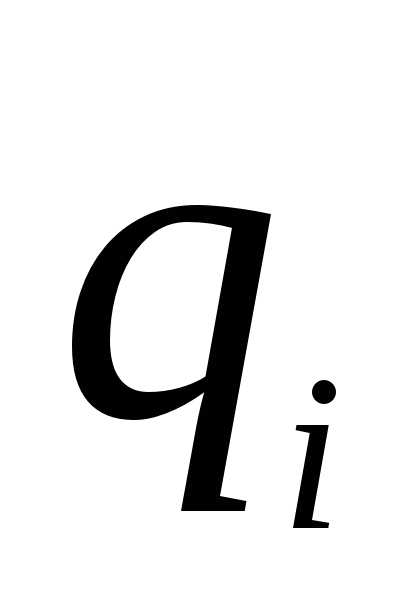 до начального положения заряда ,
до начального положения заряда ,  расстояние от заряда до конечного положения заряда .
расстояние от заряда до конечного положения заряда .
Следовательно:
 .
.
Сопоставляя это выражение с соотношением 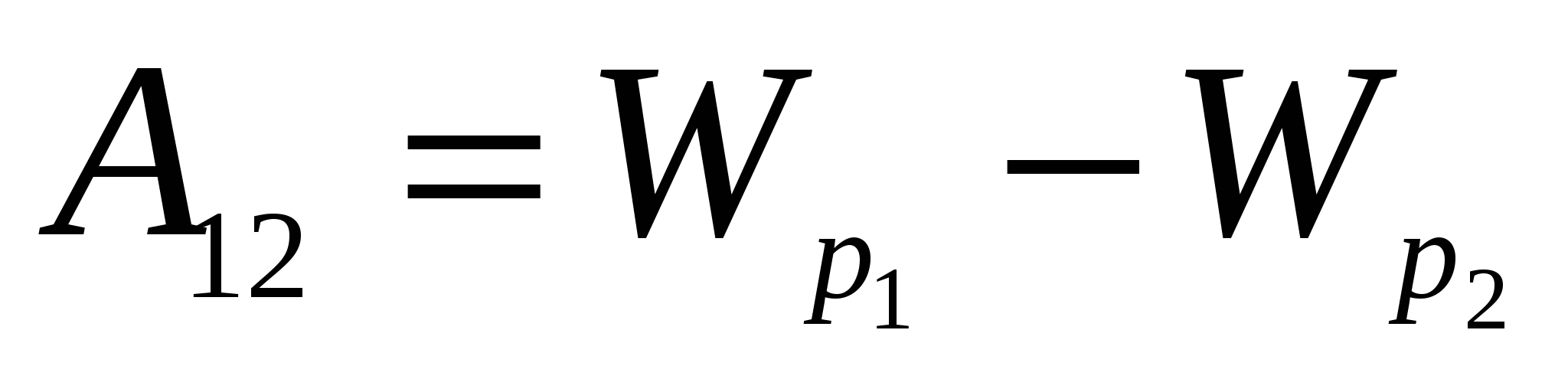 , получаем для потенциальной энергии заряда в поле системы зарядов выражение:
, получаем для потенциальной энергии заряда в поле системы зарядов выражение:
 , (10)
, (10)
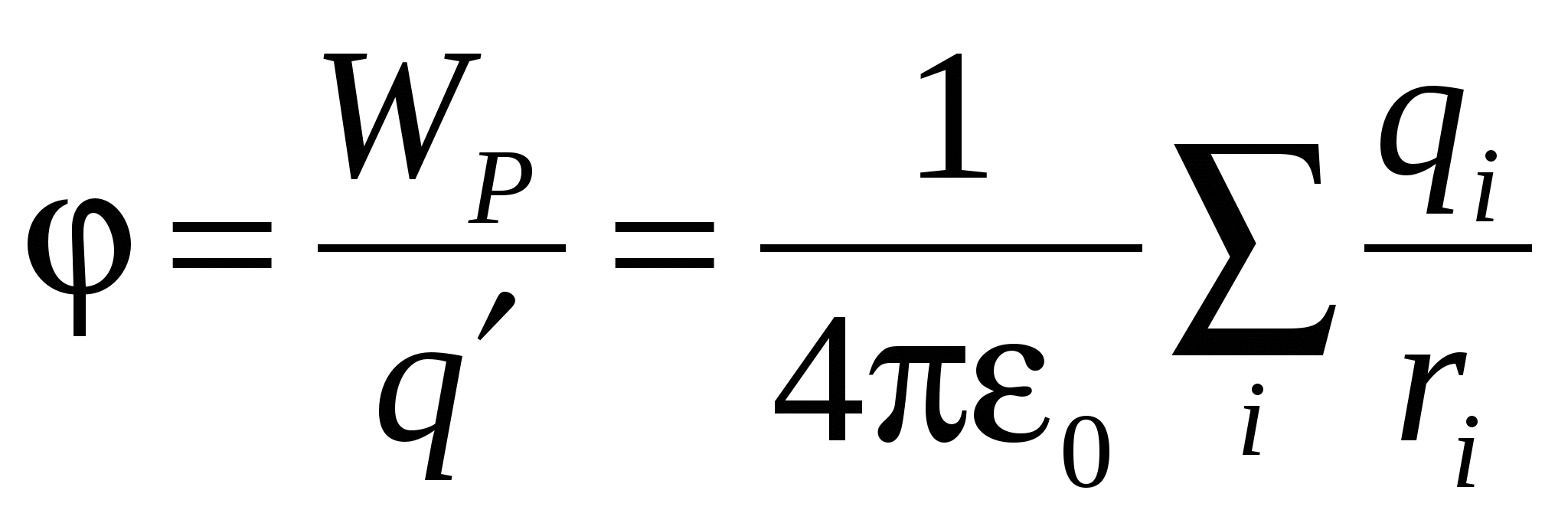 . (11).
. (11).
Следовательно, потенциал поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в отдельности.
Из соотношения 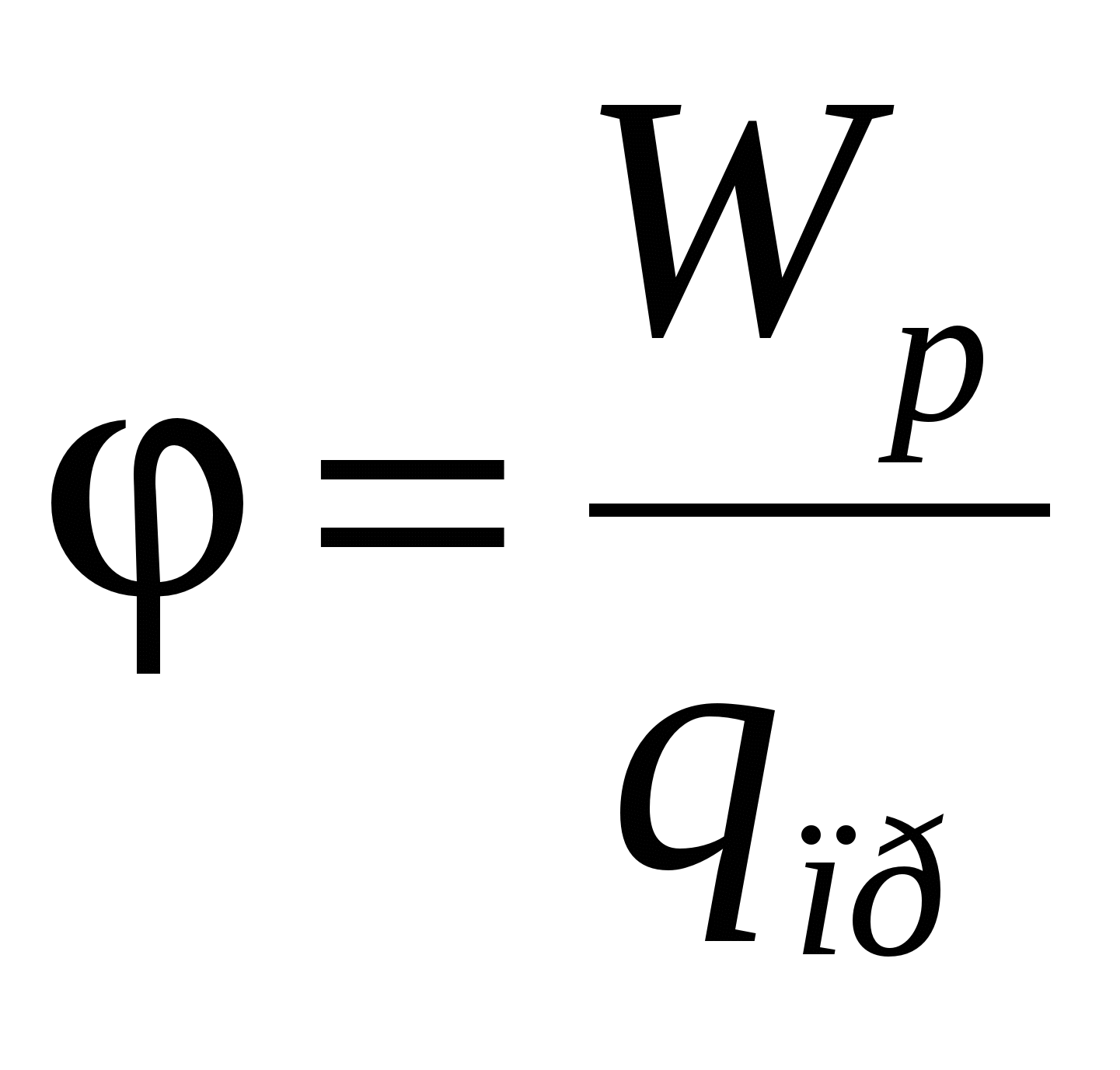 вытекает, что заряд
вытекает, что заряд  , находящийся в точке поля с потенциалом
, находящийся в точке поля с потенциалом  , обладает потенциальной энергией
, обладает потенциальной энергией  . Следовательно, работа сил поля над зарядом может быть выражена через разность потенциалов:
. Следовательно, работа сил поля над зарядом может быть выражена через разность потенциалов:
Таким образом, работа, совершаемая над зарядом силами поля , равна произведению заряда на разность потенциалов в начальной и конечной точках. Если заряд из точки с потенциалом удаляется на бесконечность (где по условию потенциал равен нулю), работа сил поля будет равна
 или
или 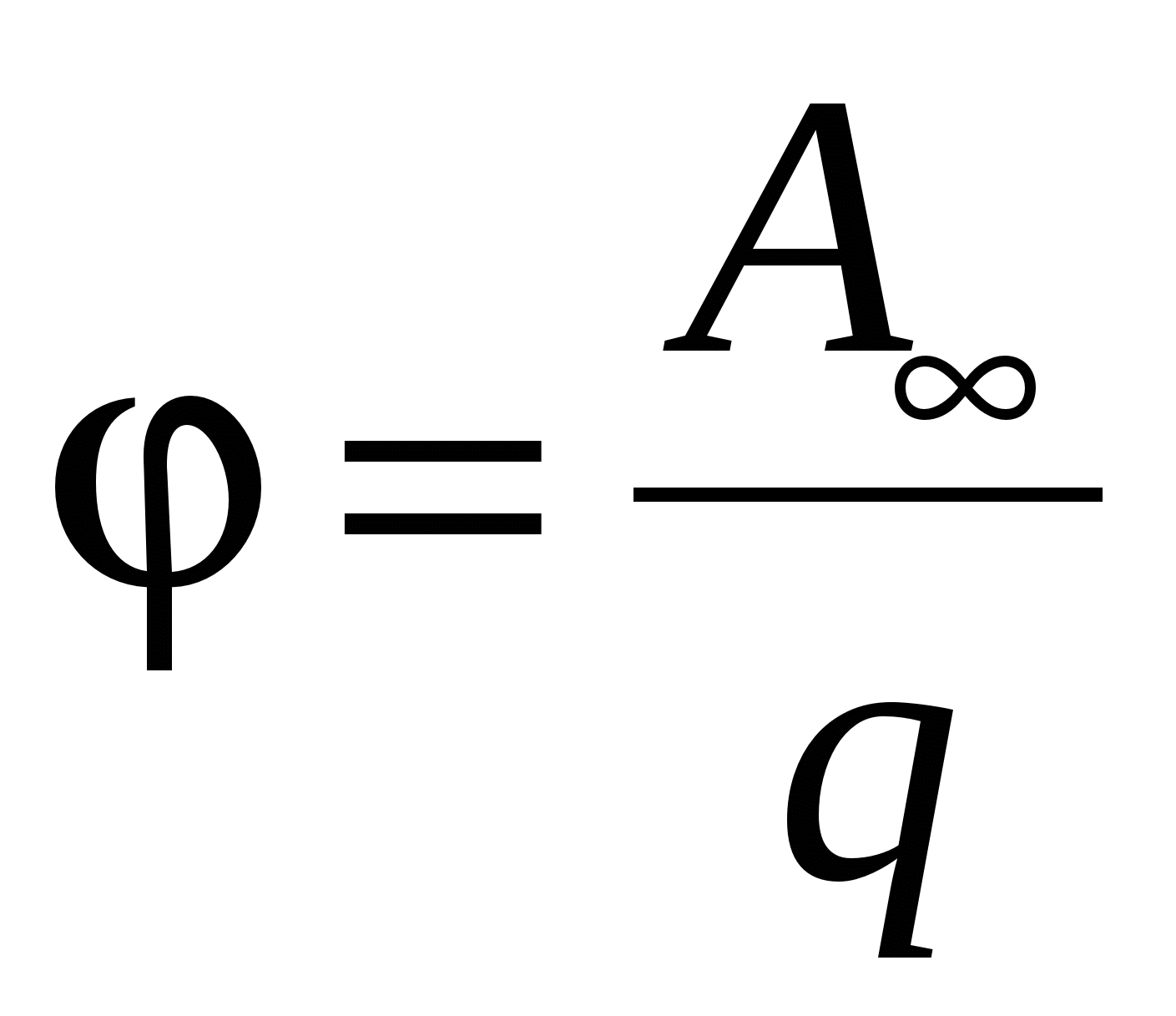 ,
,
Т. е, потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при удалении его из данной точки поля в бесконечность, или работе, которую надо совершить против сил электрического поля для того, чтобы переместить единичный положительный заряд из бесконечности в данную точку поля .
За единицу потенциала следует принять потенциал в такой точке поля, для перемещения заряда в которую из бесконечности необходимо совершить работу, равную
1 Джоулю (система единиц “Си”)

Отсюда 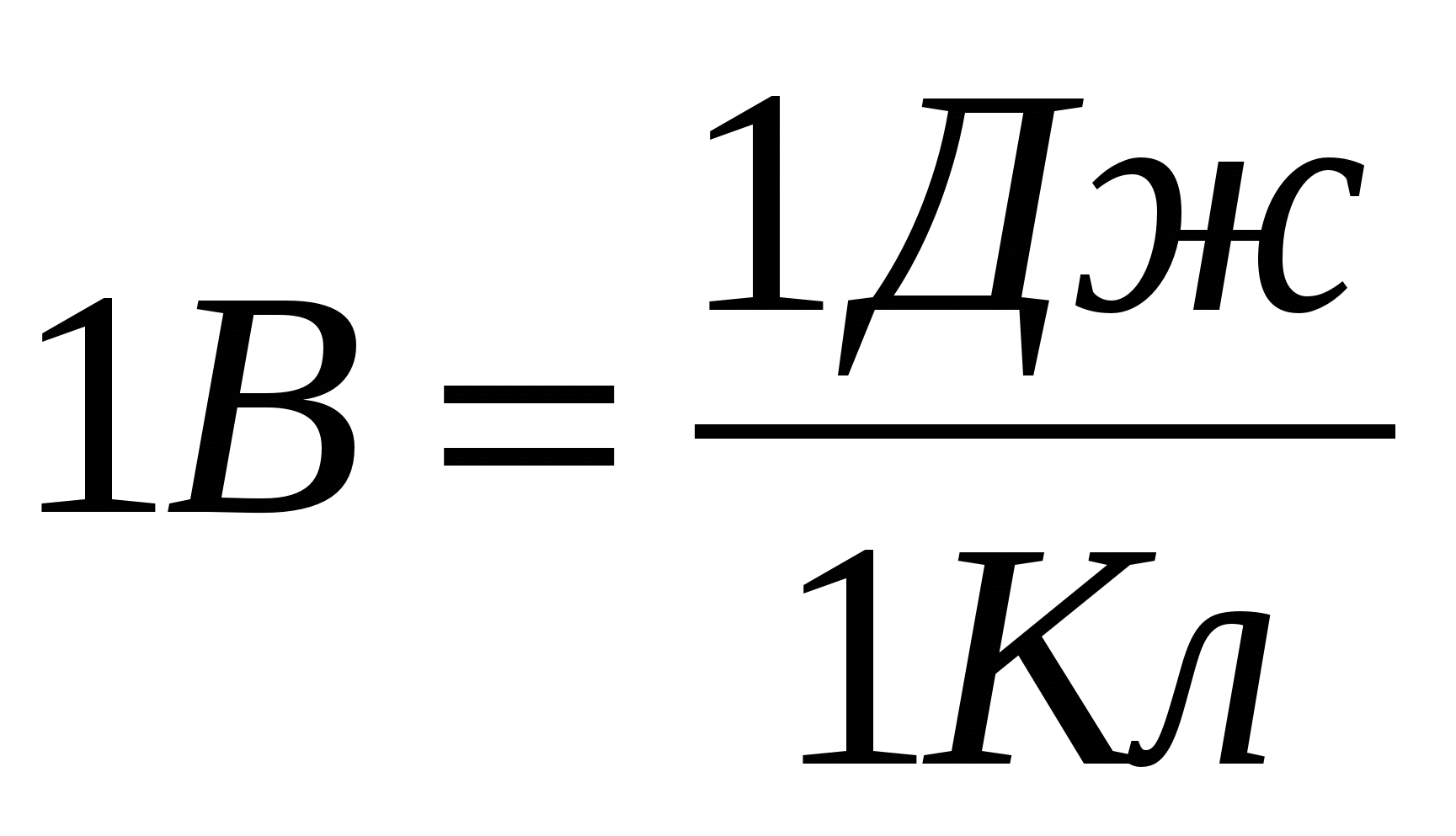 .
.
3.4. Диполь в электростатическом поле
Э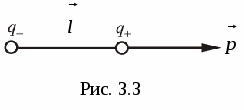 лектрическим диполем
называется совокупность двух равных зарядов противоположного знака, находящихся друг от друга на расстоянии l
, малом по сравнению с их расстоянием до точек, в которых определяется поле диполя.
лектрическим диполем
называется совокупность двух равных зарядов противоположного знака, находящихся друг от друга на расстоянии l
, малом по сравнению с их расстоянием до точек, в которых определяется поле диполя.
Произведение заряда на расстояние между зарядами р=
ql
называется дипольным моментом
. Для полного определения диполя нужно задать еще и ориентацию оси диполя в пространстве. В соответствии с этим дипольный момент следует рассматривать как вектор  . Этому вектору приписывают направление от отрицательного заряда к положительному
(рис.3.3). Если ввести радиус – вектор
. Этому вектору приписывают направление от отрицательного заряда к положительному
(рис.3.3). Если ввести радиус – вектор  проведенный от –q
к +q
, то дипольный момент можно представить в виде:
проведенный от –q
к +q
, то дипольный момент можно представить в виде:
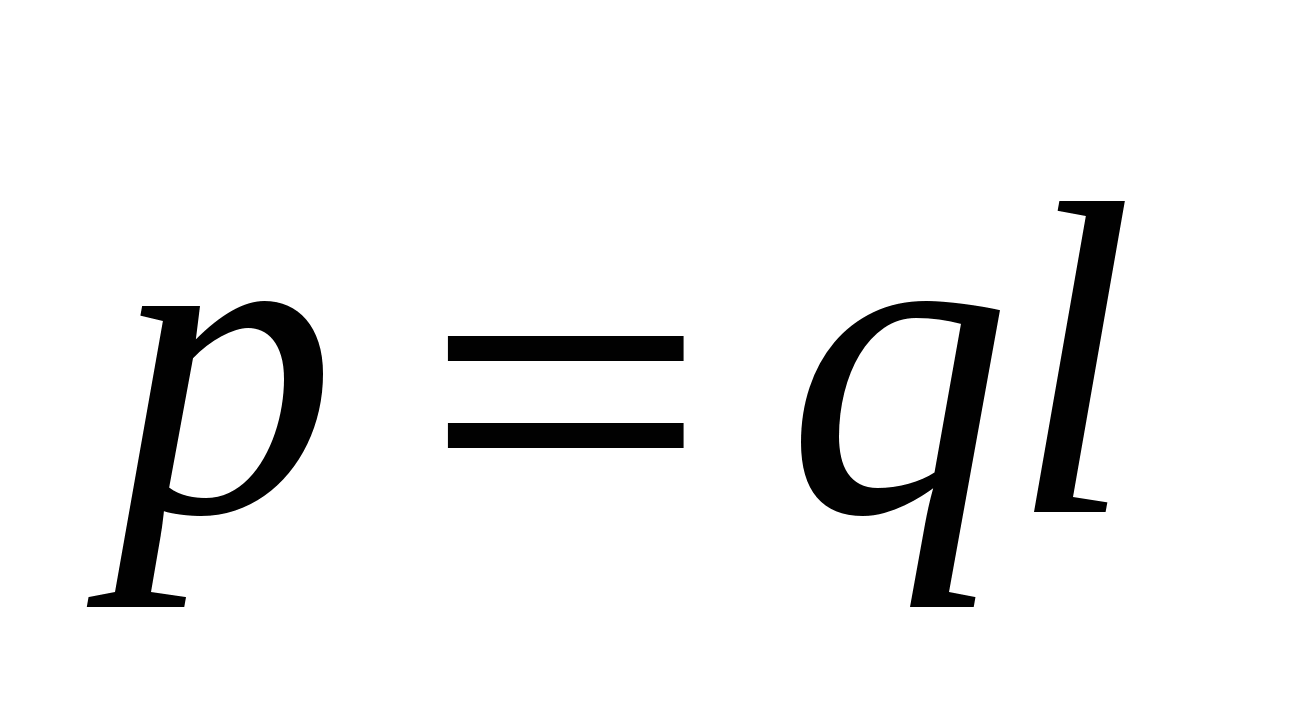 .
(13)
.
(13)
Если диполь поместить в однородное электрическое поле, образующие диполь заряды –q
и +q
окажутся под действием равных по величине, но противоположных по направлению сил  и
и (рис. 14). Эти силы образуют пару сил, плечо которой равно
(рис. 14). Эти силы образуют пару сил, плечо которой равно 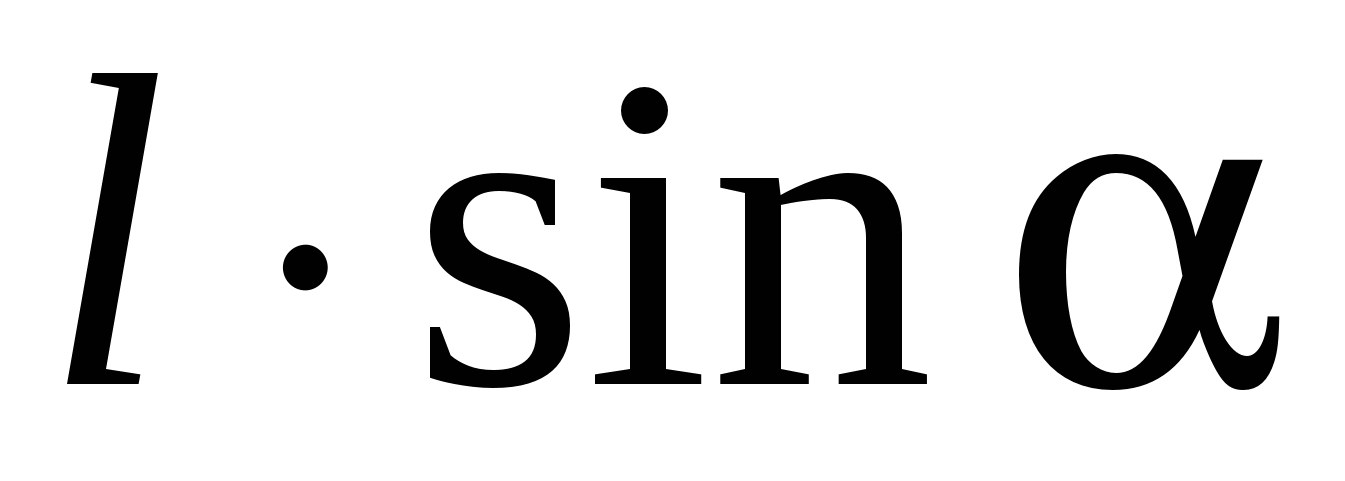 , т.е., зависит от ориентации диполя относительно поля. Модуль каждой из сил равен qE
. Умножив его на плечо, получим значение момента пары сил, действующих на диполь:
, т.е., зависит от ориентации диполя относительно поля. Модуль каждой из сил равен qE
. Умножив его на плечо, получим значение момента пары сил, действующих на диполь:
Где р – электрический момент диполя.
В векторном виде:
векторном виде:
 .
(15)
.
(15)
Момент  стремится повернуть диполь так, чтобы его момент
стремится повернуть диполь так, чтобы его момент  установился по направлению поля.
установился по направлению поля.
Чтобы увеличить угол между векторами и на dα нужно совершить работу против сил, действующих на диполь:
Эта работа идет на увеличение потенциальной энергии W , которой обладает диполь в электрическом поле, т.е.:
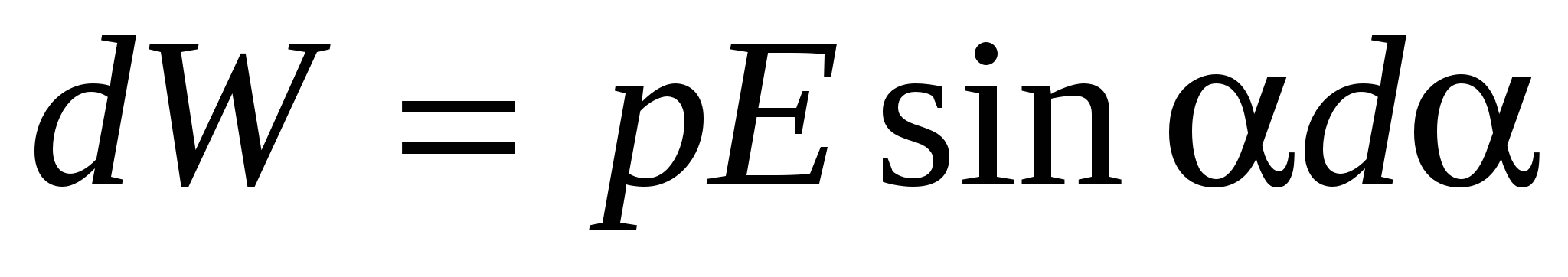 (16)
(16)
Интегрирование (16) дает для потенциальной энергии диполя в электрическом поле выражение:
Полагая const =0 , получим
В ыбрав const
=0
, считаем, что энергия диполя будет равна нулю, когда диполь устанавливается перпендикулярно к направлению поля. Наименьшее значение энергии, равное (-рЕ)
, получается при ориентации диполя по направлению поля, наибольшее, равное рЕ
, когда направлен в сторону, противоположную по направлению вектору
.
ыбрав const
=0
, считаем, что энергия диполя будет равна нулю, когда диполь устанавливается перпендикулярно к направлению поля. Наименьшее значение энергии, равное (-рЕ)
, получается при ориентации диполя по направлению поля, наибольшее, равное рЕ
, когда направлен в сторону, противоположную по направлению вектору
.
В неоднородном поле силы, действующие на заряды диполя, не одинаковы. При малых размерах диполя силы f
1 и
f
2 можно считать приближенно коллинеарными. Предположим, что поле изменяется быстрее всего в направлении х
, совпадающем с направлением
в том месте, где расположен диполь (рис. 3.5). Положительный заряд диполя смещен относительно отрицательного в направлении х
на величину 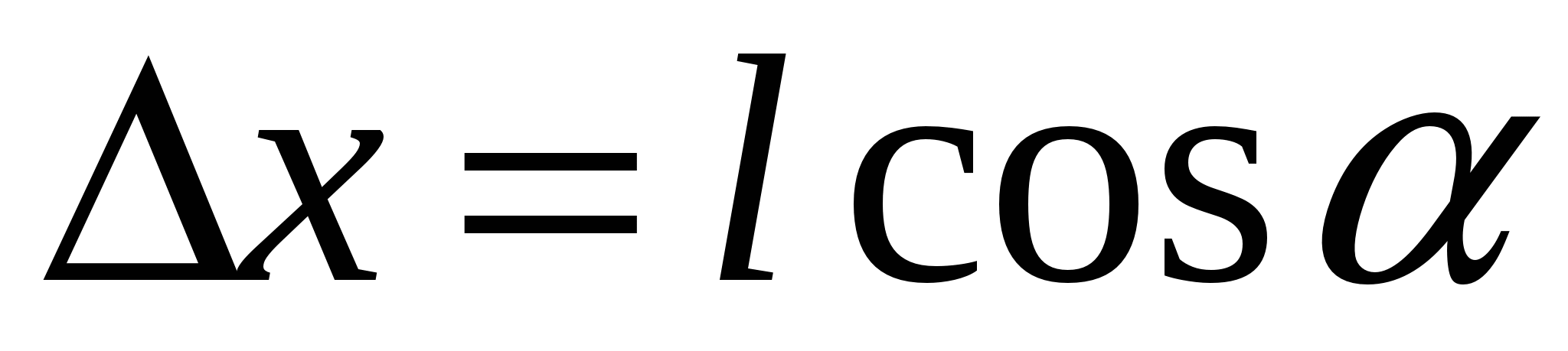 . Поэтому напряженность поля в точках, где помещаются заряды, отличается на ΔЕ
. Так как сумма сил
. Поэтому напряженность поля в точках, где помещаются заряды, отличается на ΔЕ
. Так как сумма сил  и
и 
 или ,
(19)
или ,
(19)
 , то
, то
 , (20)
, (20)
Где  – градиент вектора напряженности электрического поля. Таким образом, в неоднородном электрическом поле, кроме вращающегося момента, действует сила f
, под действием которой диполь будет либо втягиваться в область более сильного поля (α 0), либо выталкиваться из нее (α>90 0).
– градиент вектора напряженности электрического поля. Таким образом, в неоднородном электрическом поле, кроме вращающегося момента, действует сила f
, под действием которой диполь будет либо втягиваться в область более сильного поля (α 0), либо выталкиваться из нее (α>90 0).
Выражение для силы можно получить из (18), учтя, что f
= – .
.
3.5. Связь между напряженностью электростатического поля и потенциалом
Напряженность электрического поля – величина, численно равная силе, действующей на заряд . Потенциал – величина, численно равная потенциальной энергии заряда . Таким образом, между этими величинами должна существовать связь, аналогичная связи между потенциальной энергией и силой (т.е.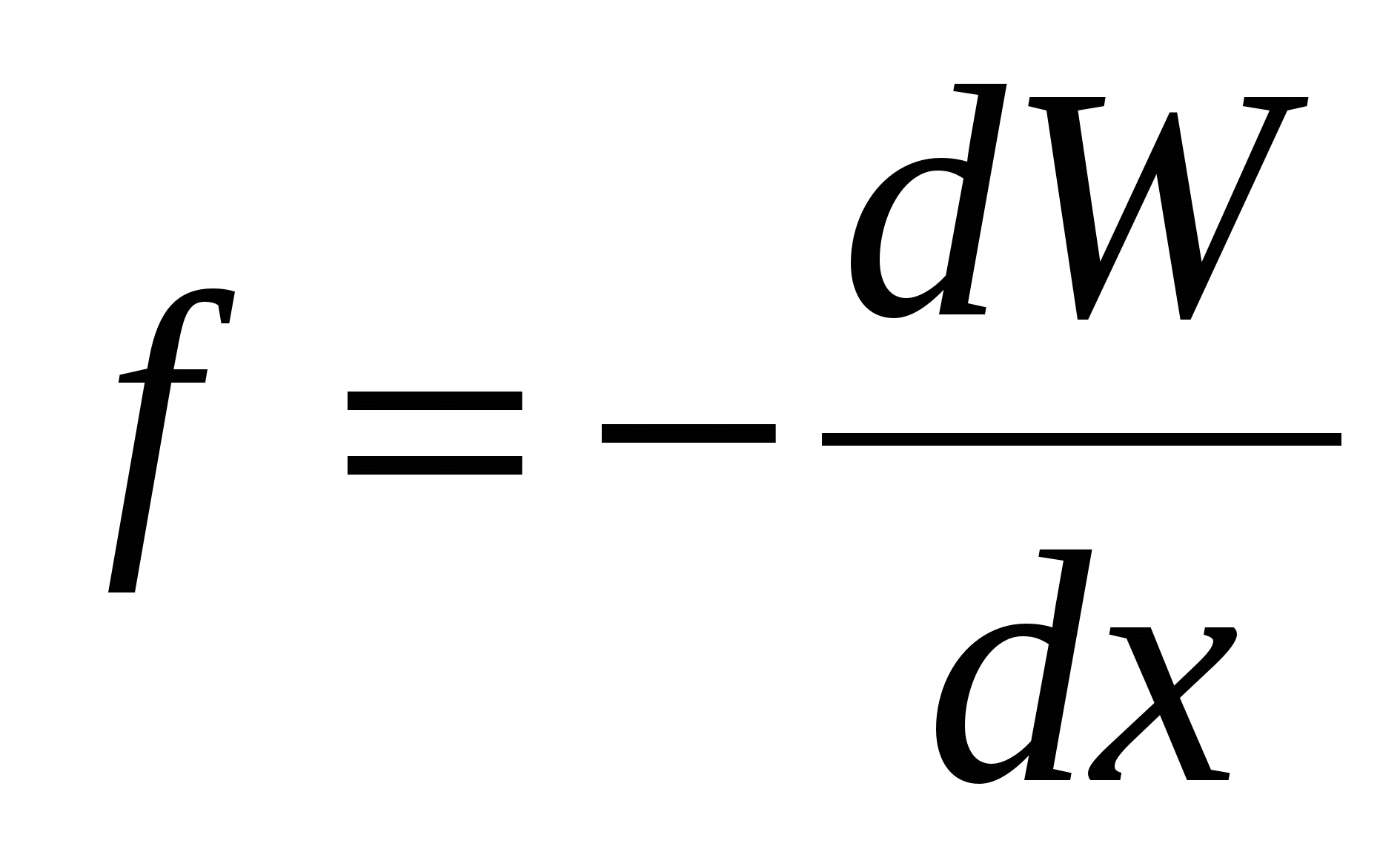 ). Работа сил поля над зарядом на отрезке пути может быть представлена как
). Работа сил поля над зарядом на отрезке пути может быть представлена как  , а убыль потенциальной энергии заряда, которая при этом будет возникать: . Откуда из равенства
, а убыль потенциальной энергии заряда, которая при этом будет возникать: . Откуда из равенства  находим:
находим: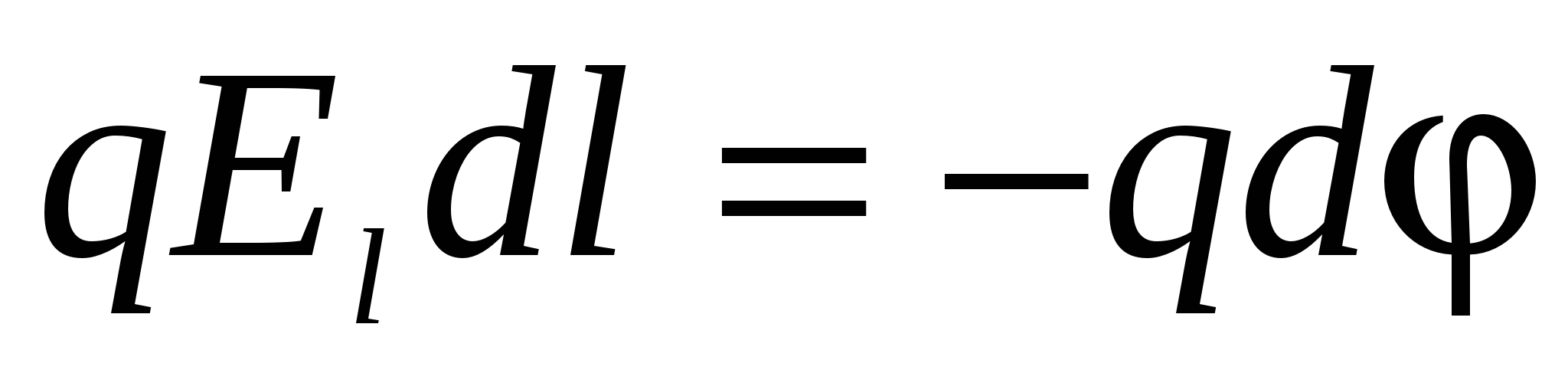 или
или 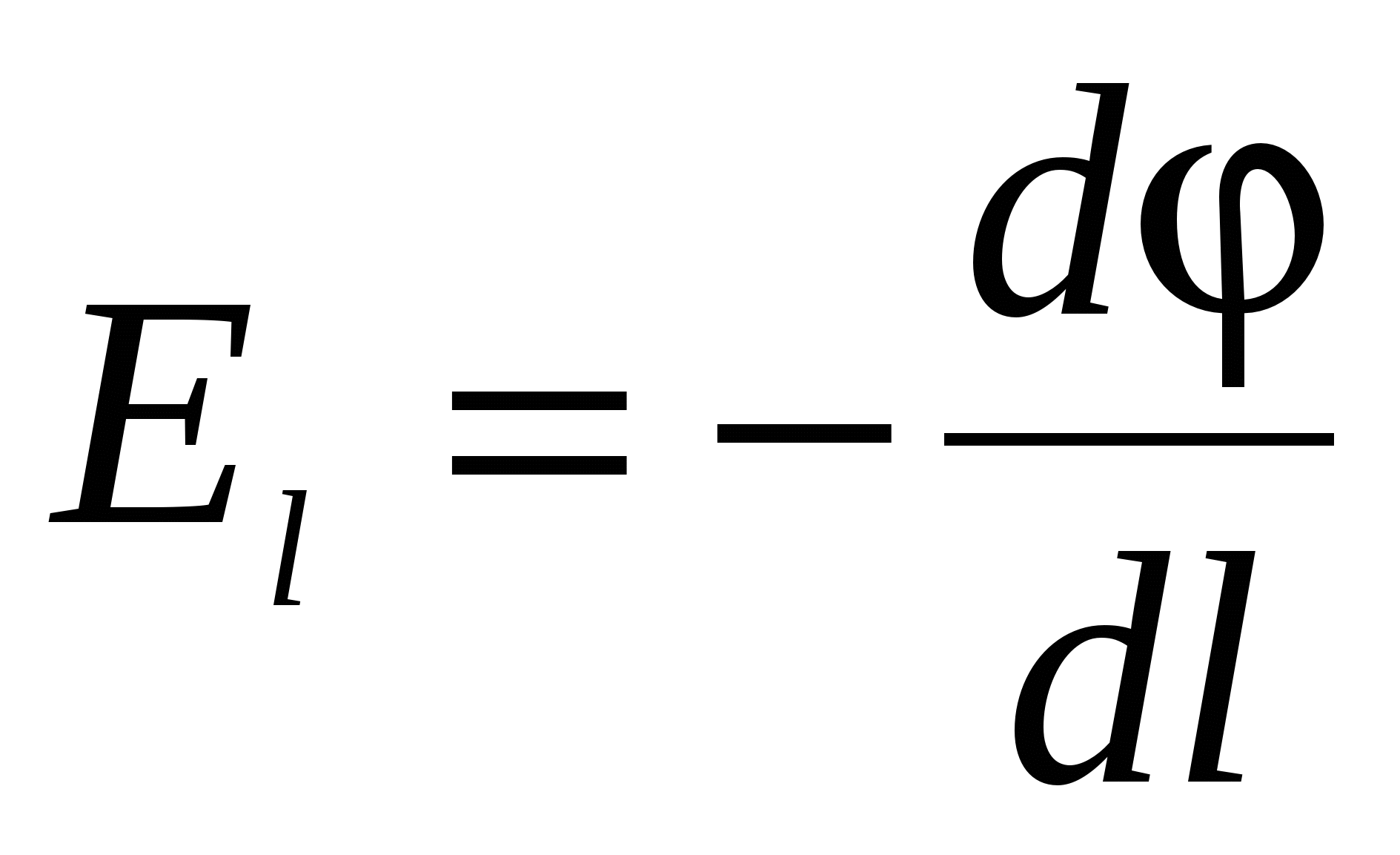 , (21)
, (21)
Где через  обозначено произвольно выбранное направление.
обозначено произвольно выбранное направление.
 ,
, 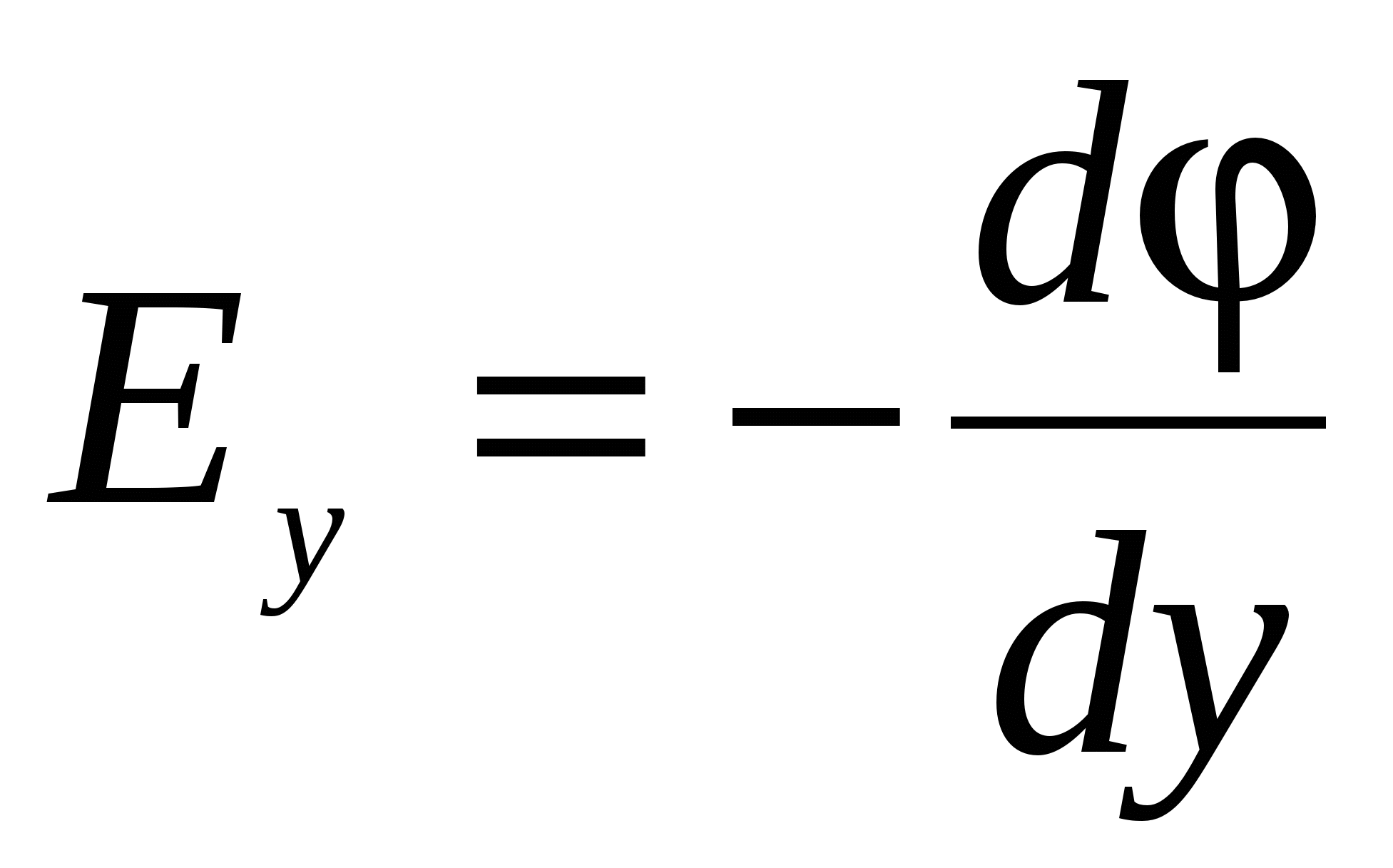 ,
,  , (22)
, (22)
Где орты координатных осей, т. е., единичные вектора. Вектор с компонентами
орты координатных осей, т. е., единичные вектора. Вектор с компонентами 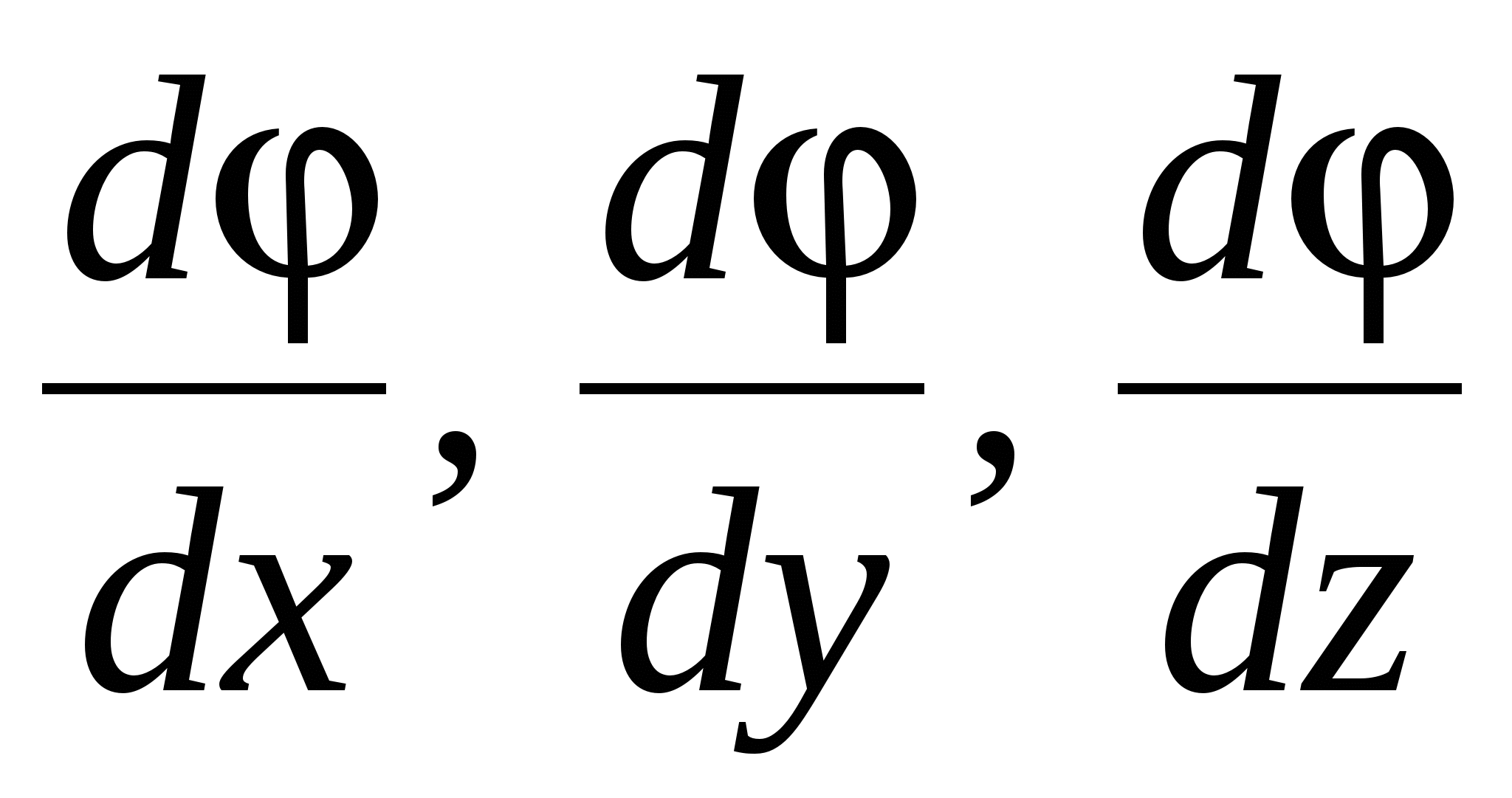 , где
, где  скалярная функция координат
скалярная функция координат  называется градиентом
функции и обозначается символом
называется градиентом
функции и обозначается символом  (или
(или 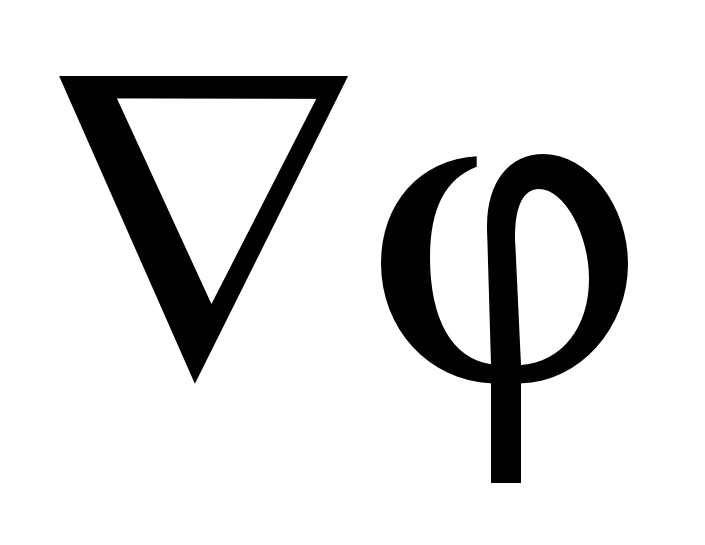 , где
, где  – оператор набла). Таким образом, градиент потенциала:
– оператор набла). Таким образом, градиент потенциала:
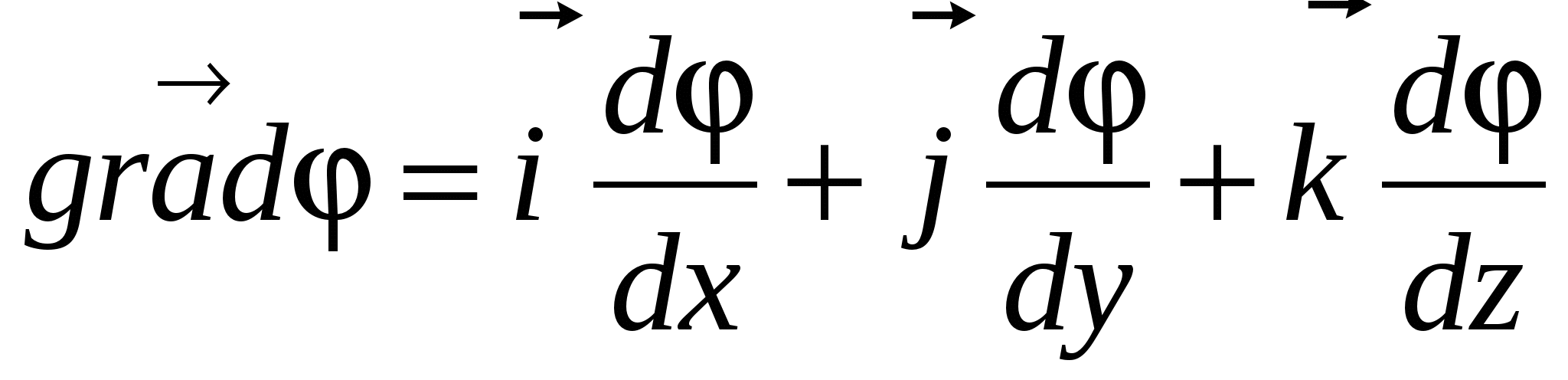 (24)
(24)
И из (23) и (24) следует, что
 (25)
(25)
Так как градиент – это вектор, показывающий направление наискорейшего изменения некоторой величины, значение которой меняется от одной точки пространства к другой, то градиентом потенциала 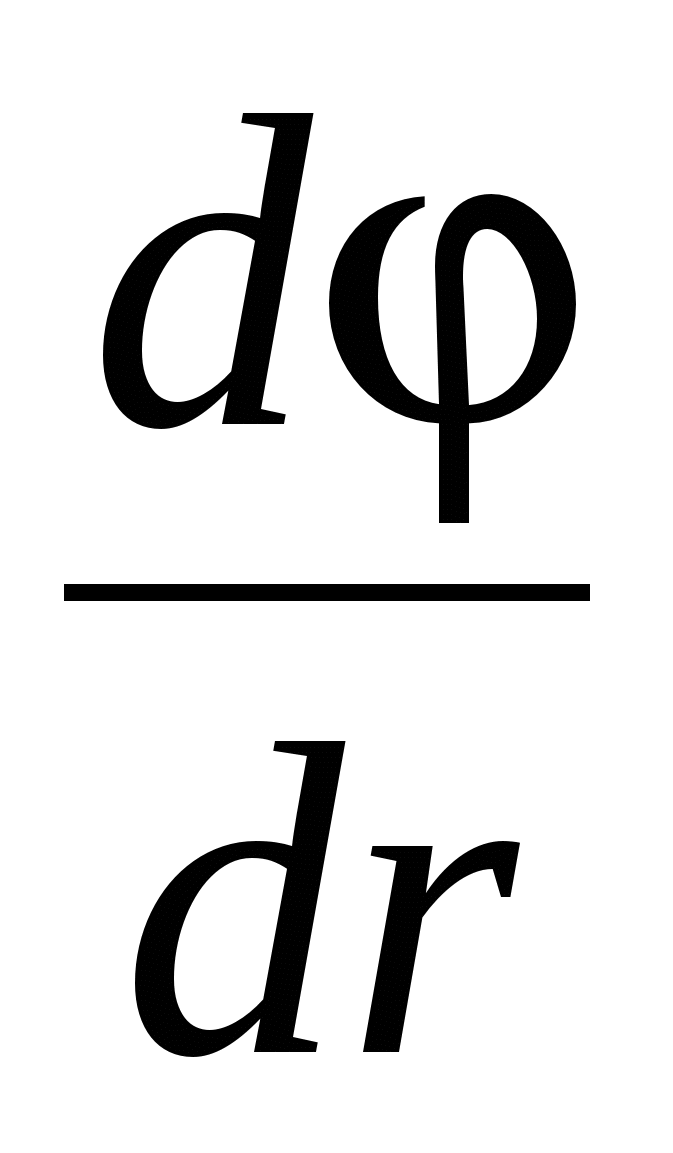 (где r
–радиус-вектор) называется вектор, направленный в сторону наиболее быстрого возрастания потенциала, численно равный быстроте его изменения на единицу длины в этом направлении.
(где r
–радиус-вектор) называется вектор, направленный в сторону наиболее быстрого возрастания потенциала, численно равный быстроте его изменения на единицу длины в этом направлении.
Поскольку 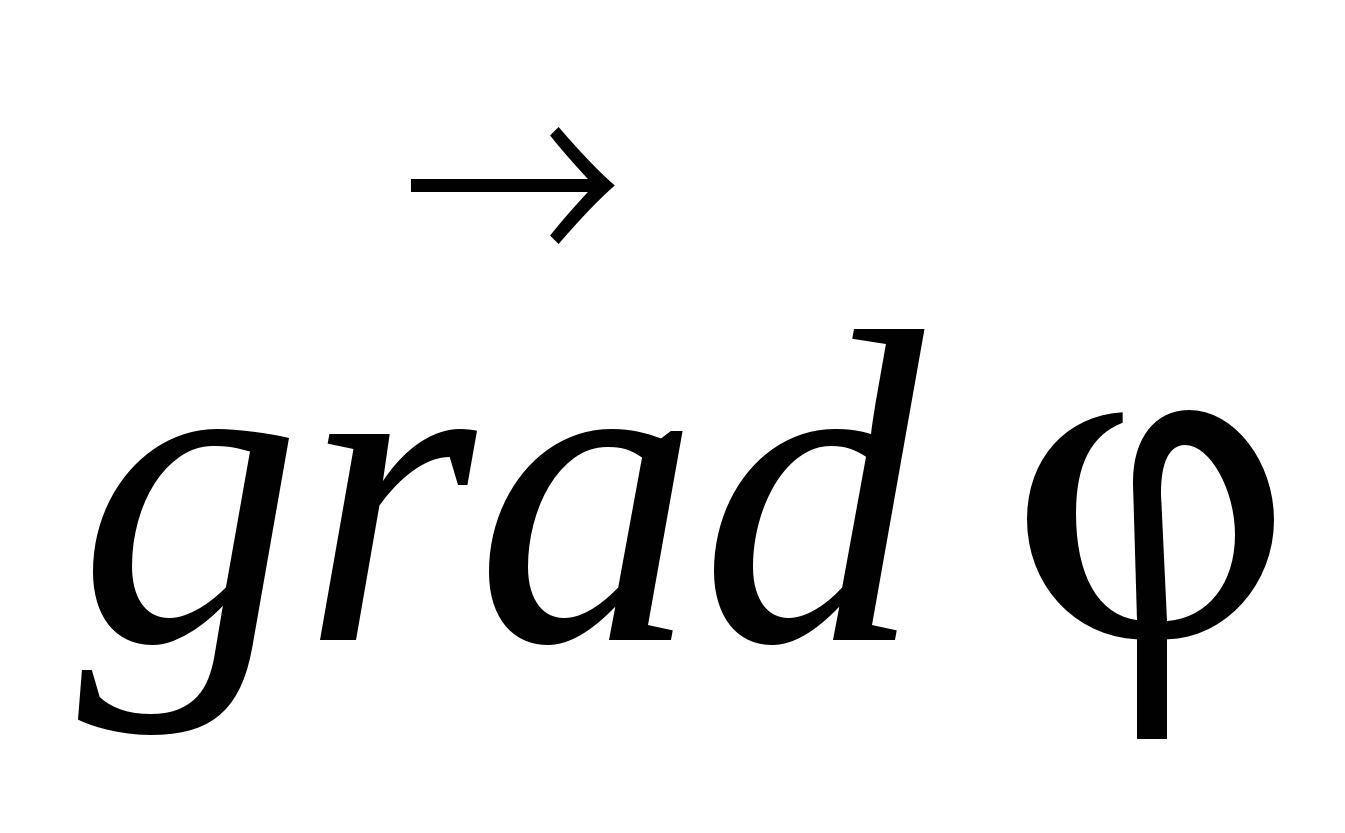 – векторная величина, то его модуль выражается как:
– векторная величина, то его модуль выражается как:
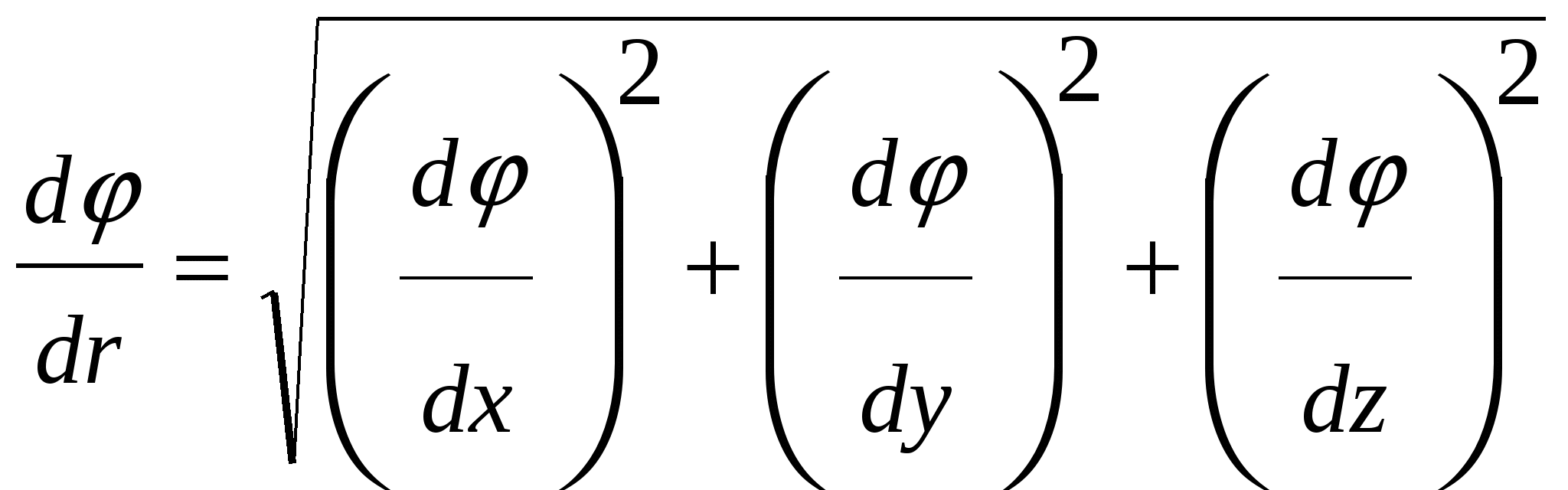 , (26)
, (26)
Подобно тому, как модуль вектора 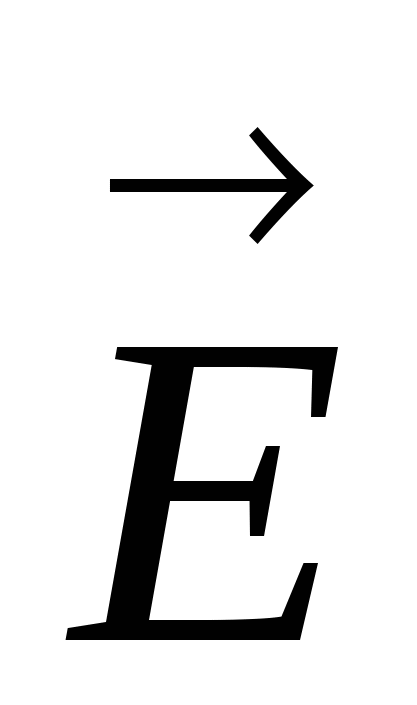 :
:
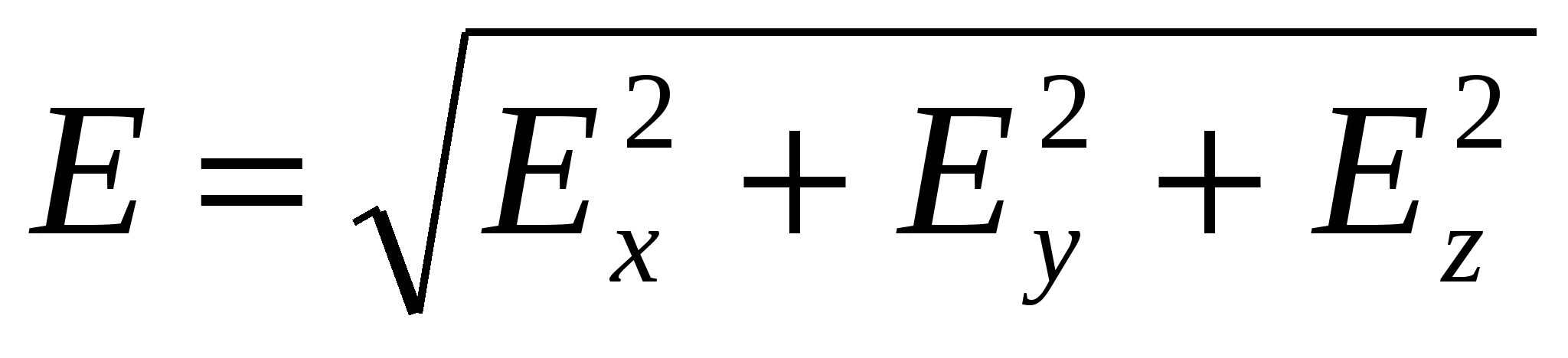 (27)
(27)
Знак “–” (25) указывает на то, что напряженность направлена в сторону убывания потенциала. Формула (25) позволяет по известным значениям найти напряженность поля в каждой точке или решить обратную задачу, т.е., по заданным значения в каждой точке найти разность потенциалов между двумя произвольными точками поля.
3.6. Эквипотенциальные поверхности
Потенциал электростатического поля представляет собой функцию, меняющуюся от точки к точке. Однако, во всяком реальном случае можно выделить совокупность точек, потенциалы которых одинаковы.Г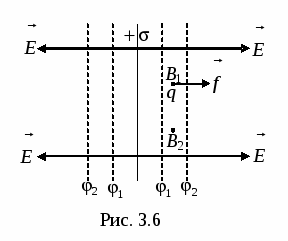 еометрическое место точек постоянного потенциала называется поверхностью равного потенциала или эквипотенциальной поверхностью.
еометрическое место точек постоянного потенциала называется поверхностью равного потенциала или эквипотенциальной поверхностью.
Возьмем равномерно заряженную бесконечную плоскость (рис. 3.6). Поле, создаваемое такой плоскостью однородно, а линии напряженности нормальны к плоскости. Отсюда следует, что работа перемещения заряда из некоторой точки В 1 в любую другую точку В 2 , находящуюся на таком же расстоянии от заряженной поверхности, что и точка В 1 равна нулю. Действительно, при перемещении некоторого заряда q по прямой В 1 В 2 сила, действующая на заряд со стороны поля, будет все время перпендикулярна к перемещению, а, следовательно, ее работа равна нулю. Но эта работа может быть представлена, с другой стороны, в виде:
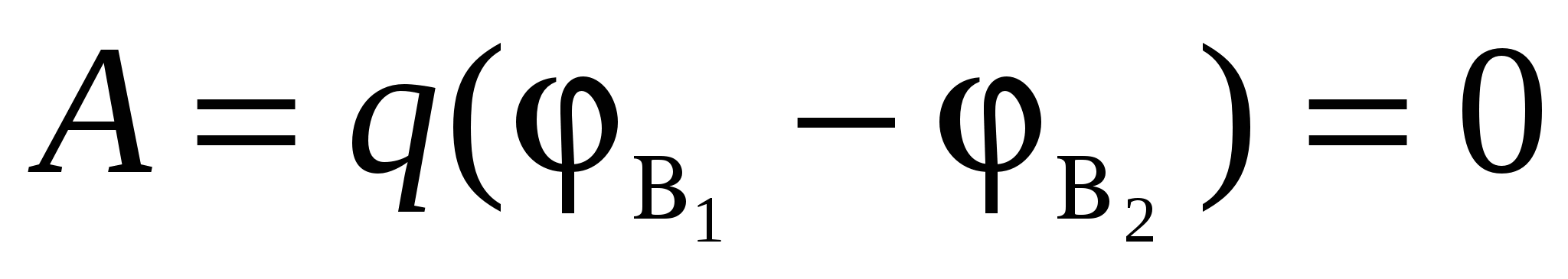 , (28)
, (28)
Г де
де  и
и  – соответственно потенциалы точек В
1
и В
2
. Отсюда, так как А =
0, то =, т.е., потенциалы точек, равноудаленных от заряженной плоскости, одинаковы. Таким образом, поверхности равного потенциала (эквипотенциальные поверхности) являются плоскостями, параллельными заряженной плоскости. Если плоскость заряжена положительно, то значение потенциала убывает по мере удаления от заряженной плоскости. Очевидно, что поверхности равного потенциала расположены симметрично по обе стороны от заряженной плоскости.
– соответственно потенциалы точек В
1
и В
2
. Отсюда, так как А =
0, то =, т.е., потенциалы точек, равноудаленных от заряженной плоскости, одинаковы. Таким образом, поверхности равного потенциала (эквипотенциальные поверхности) являются плоскостями, параллельными заряженной плоскости. Если плоскость заряжена положительно, то значение потенциала убывает по мере удаления от заряженной плоскости. Очевидно, что поверхности равного потенциала расположены симметрично по обе стороны от заряженной плоскости.
Эквипотенциальные поверхности поля точечного заряда это сферы с радиусом r
, центр которых находится в центре точечного заряда, т.е.  (рис. 3.7). На рис. 3.6 и рис. 3.7 вектор напряженности перпендикулярен эквипотенциальным поверхностям.
(рис. 3.7). На рис. 3.6 и рис. 3.7 вектор напряженности перпендикулярен эквипотенциальным поверхностям.
Покажем, что вектор напряженности перпендикулярен эквипотенциальной поверхности. Рассмотрим работу по перемещению заряда по поверхности равного потенциала на малом участке пути ∆S
(рис. 3.7). При этом, работа электрической силы  на данном пути будет:
на данном пути будет:
Где α – угол между направлением силы f
и перемещением ∆S
. С другой стороны, эта работа может быть выражена как произведение величины перемещающегося заряда на разность потенциалов в начальном и конечном положениях заряда, т.е. 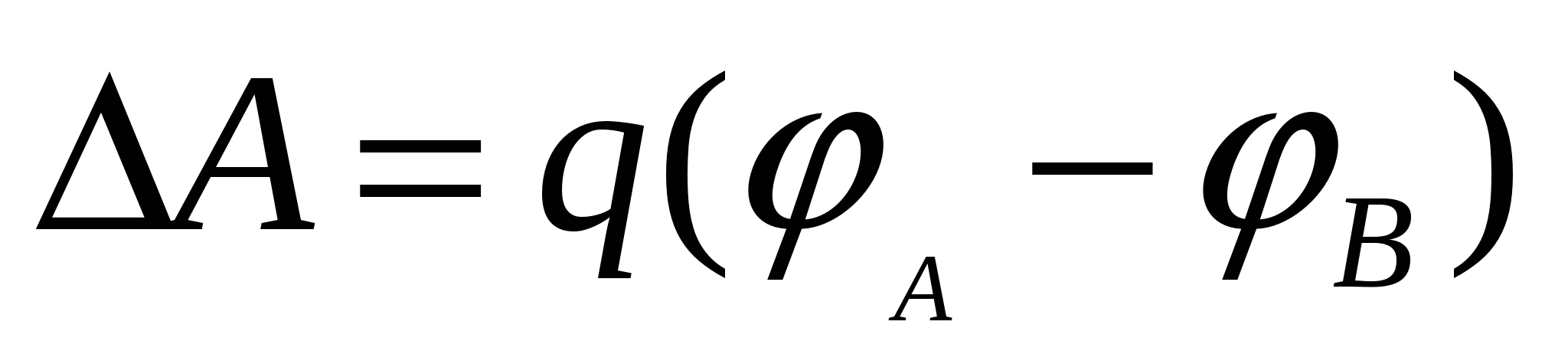 .
.
Так как перемещение идет по эквипотенциальной поверхности, то разность потенциалов 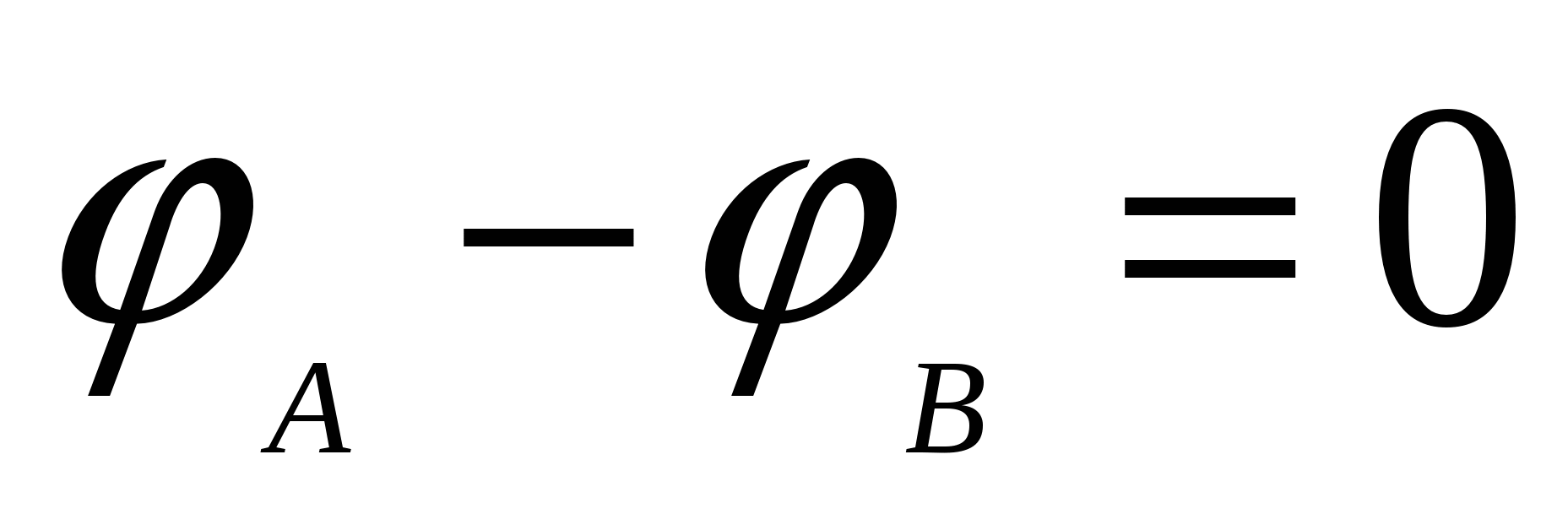 и
и  , или cosα = 0, значит α = 90 0 т.е. угол между направлением силы и перемещением ∆S
равен 90 0 . Но , т.е. направления и
совпадают, поэтому угол между
и ∆S
, α=90 0 т.е. направление вектора напряженности электростатического поля всегда перпендикулярно к эквипотенциальной поверхности.
, или cosα = 0, значит α = 90 0 т.е. угол между направлением силы и перемещением ∆S
равен 90 0 . Но , т.е. направления и
совпадают, поэтому угол между
и ∆S
, α=90 0 т.е. направление вектора напряженности электростатического поля всегда перпендикулярно к эквипотенциальной поверхности.
Эквипотенциальных поверхностей вокруг заряженного тела можно провести сколько угодно много. По густоте эквипотенциальных поверхностей можно судить о величине , однако при условии, что разность потенциалов между двумя соседними эквипотенциальными поверхностями равна постоянной величине.
Формула выражает связь потенциала с напряженностью и позволяет по известным значениям φ найти напряженность поля в каждой точке. Можно решить и обратную задачу, т.е. по известным значениям в каждой точке поля найти разность потенциалов между двумя произвольными точками поля. Для этого воспользуемся тем, что работа, совершаемая силами поля над зарядом q при перемещении его из точки 1 в точку 2, может быть, вычислена как:
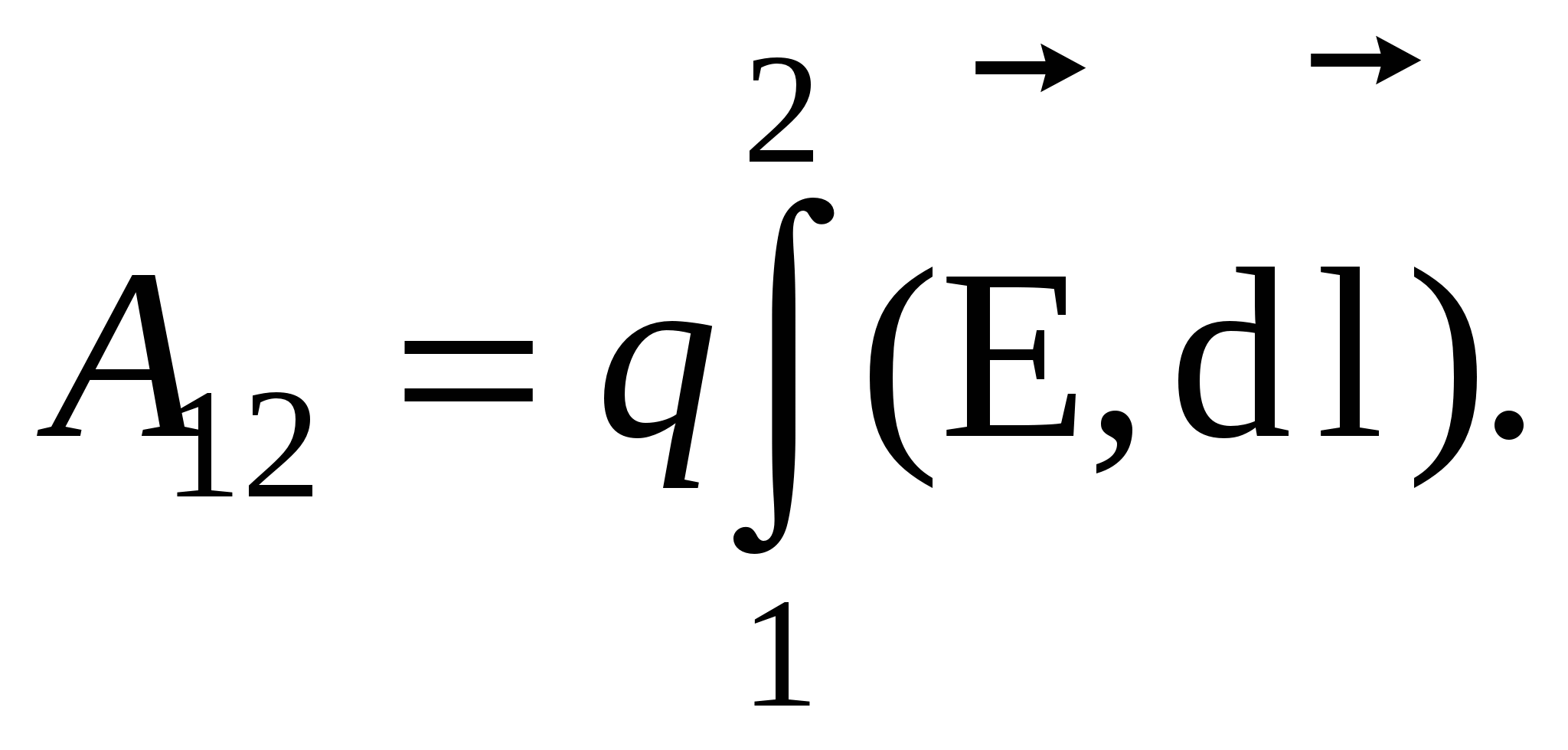
С другой стороны работу можно представить в виде:
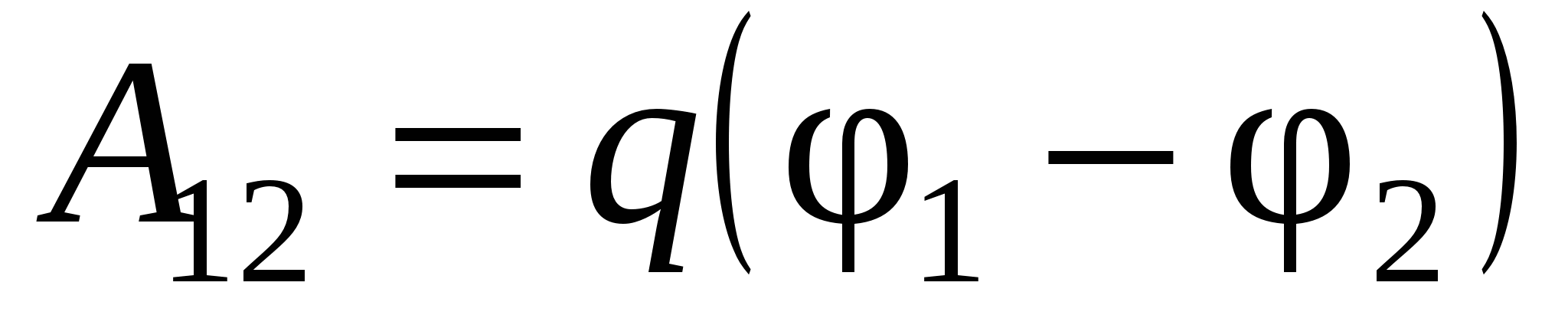 , тогда
, тогда 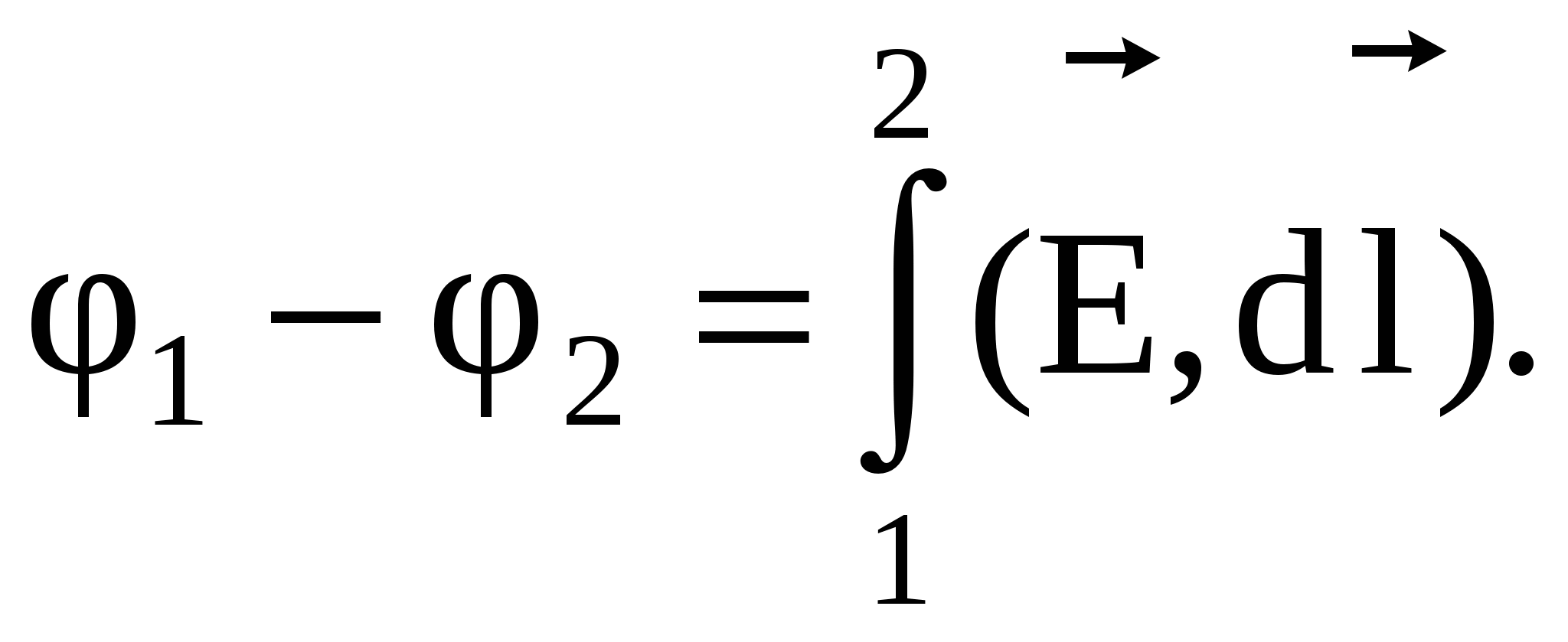
Интеграл можно брать по любой линии, соединяющие точку 1 и точку 2, т.к. работа сил поля не зависит от пути.
При обходе по замкнутому контуру 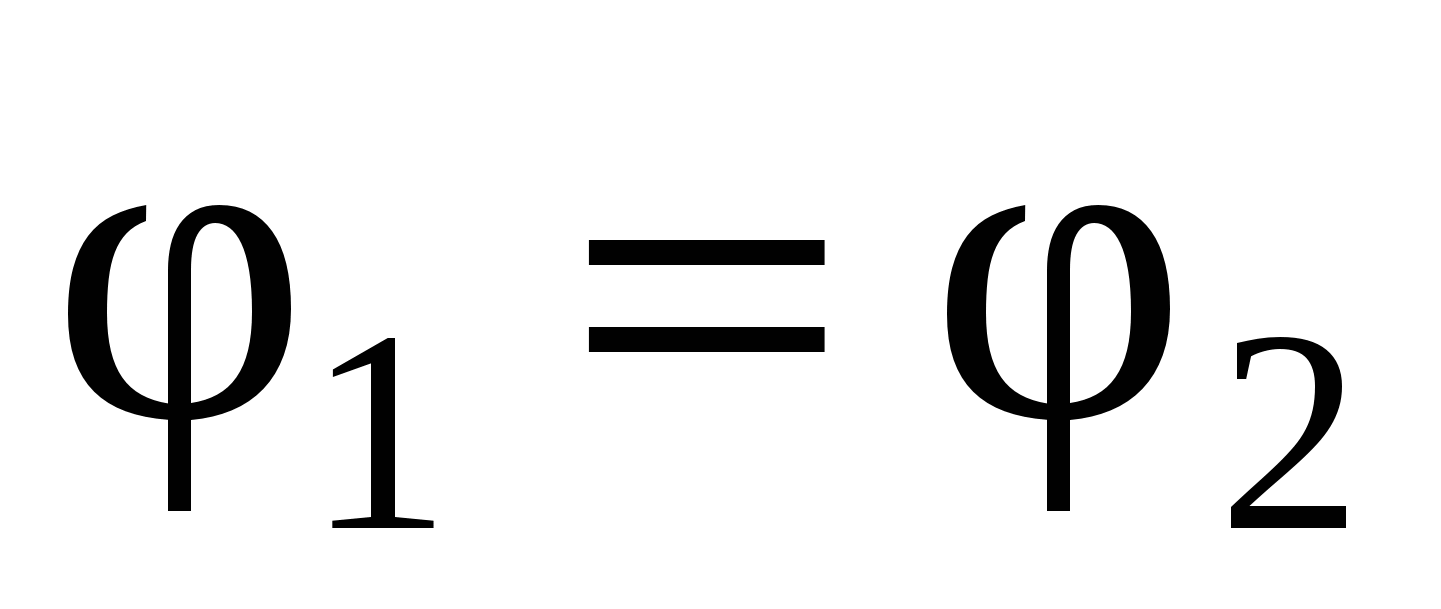 получим:
получим:

т.е. пришли к известной нам теореме о циркуляции вектора напряженности: циркуляция вектора напряженности электростатического поля вдоль любого замкнутого контура равна нулю.
Поле, обладающее этим свойством, называется потенциальным.
Из обращения в нуль циркуляции вектора следует, что линии электростатического поля не могут быть замкнутыми : они начинаются на положительных зарядах (истоки ) и на отрицательных зарядах заканчиваются (стоки ) или уходят в бесконечность .
Обобщим теорему Гаусса и теорему о циркуляции вектора напряженности электростатического поля в вакууме. Так как , а 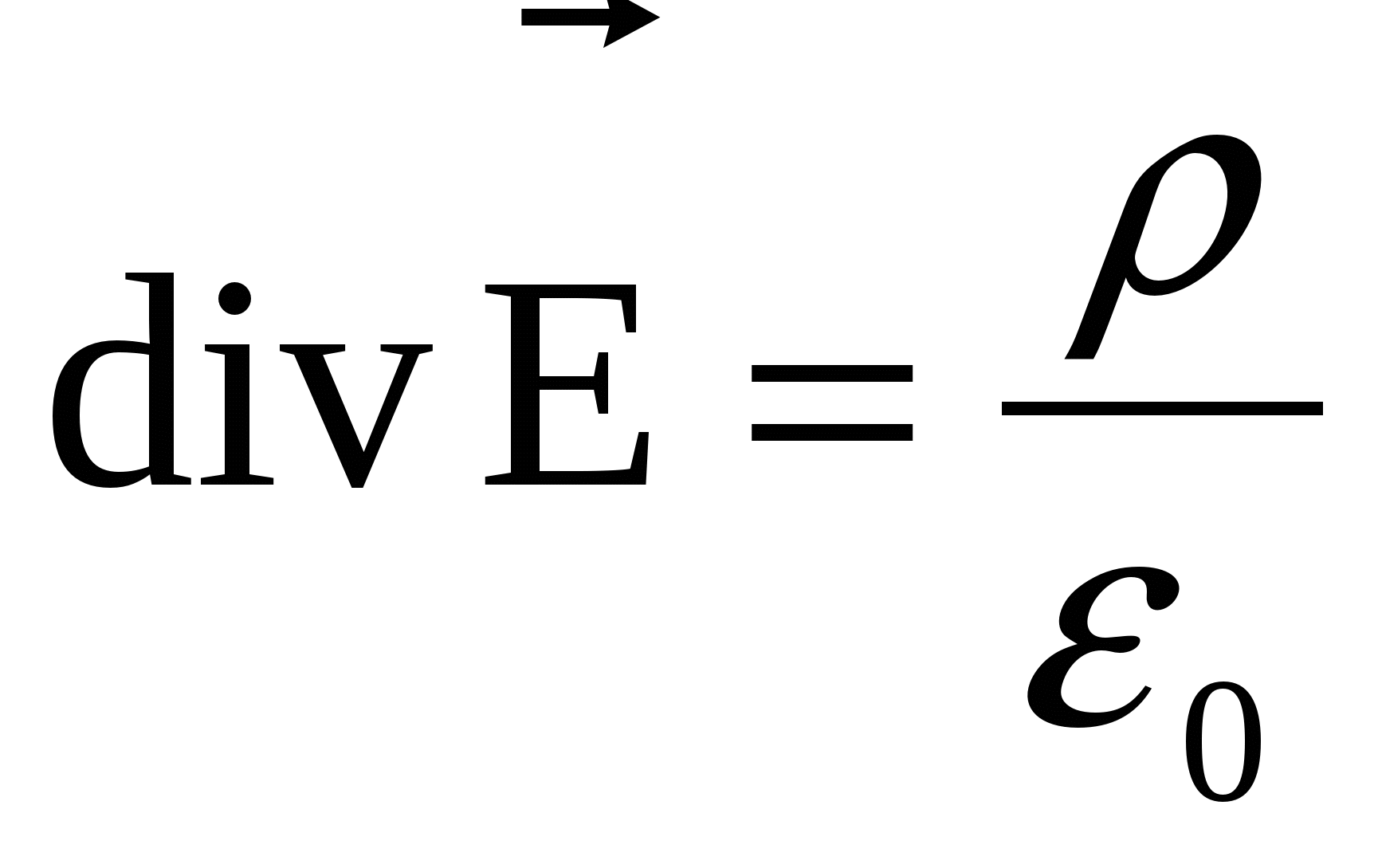 , то
, то 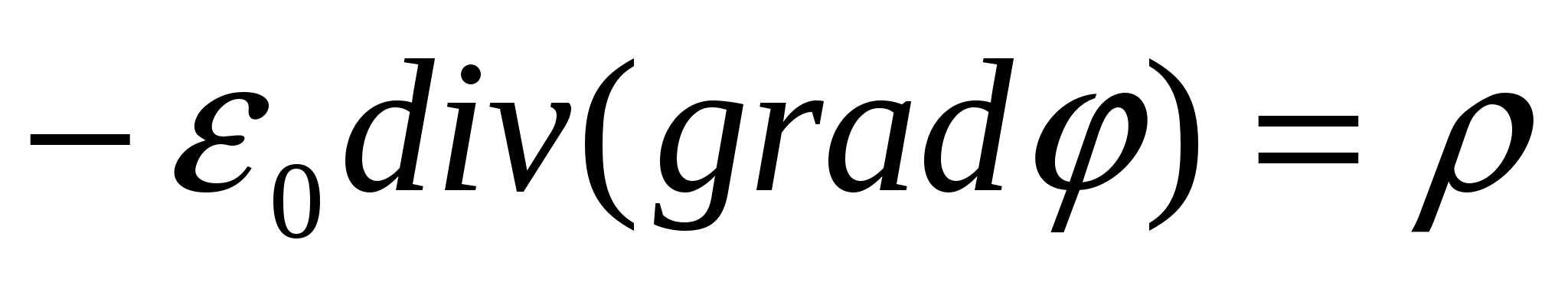 . Поскольку
. Поскольку  (
( - оператор Лапласа), то для потенциала φ получим выражение
- оператор Лапласа), то для потенциала φ получим выражение  или
или  , которое называется уравнением Пуассона
.
, которое называется уравнением Пуассона
.
Это уравнение позволяет по известному распределению заряда 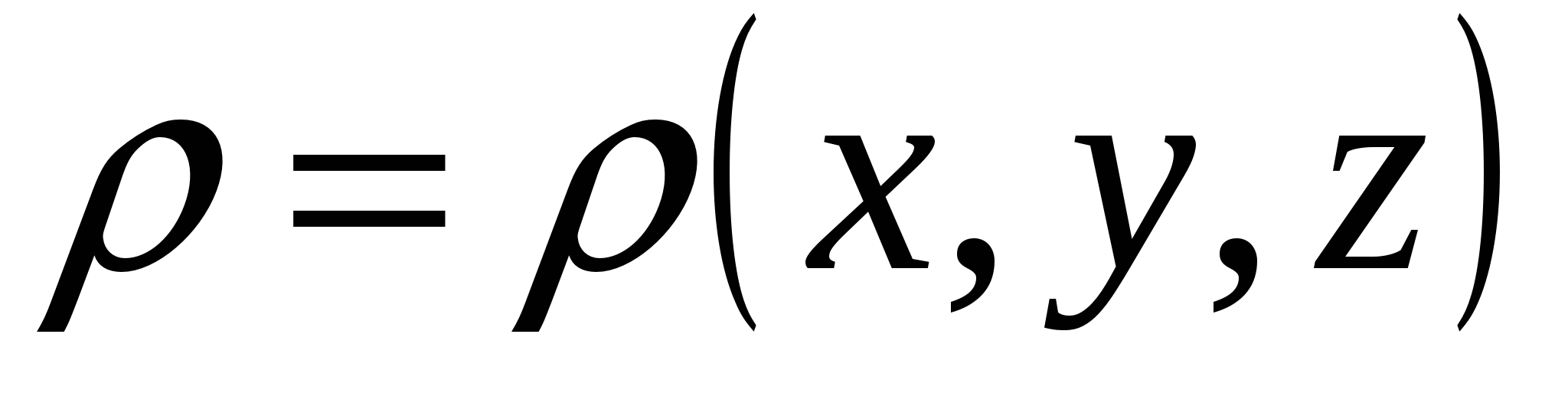 и заданным граничным условием для потенциала φ определить значения
и заданным граничным условием для потенциала φ определить значения 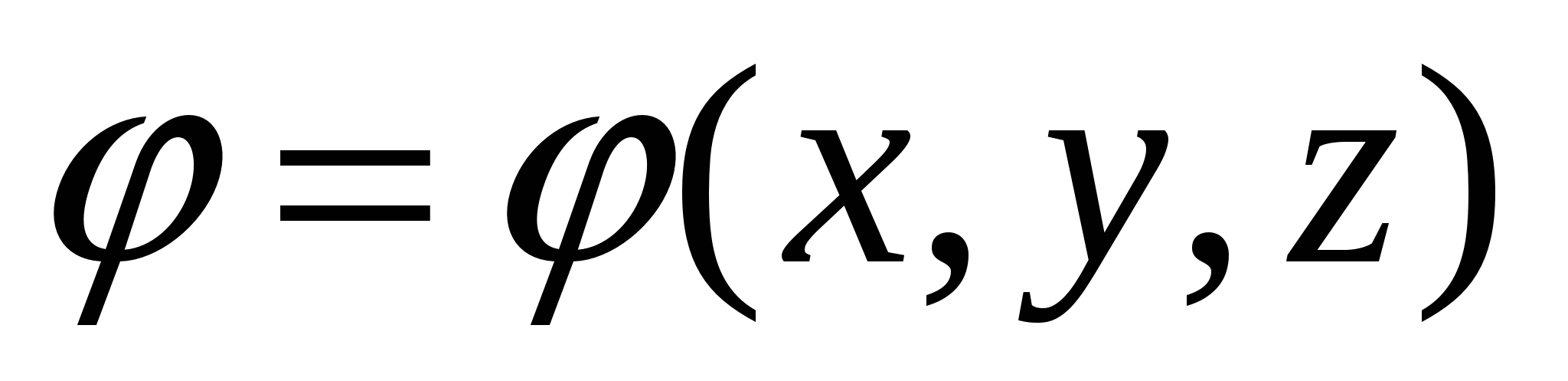 во всех точках поля, а затем по формуле найти напряженность
во всех точках поля, а затем по формуле найти напряженность 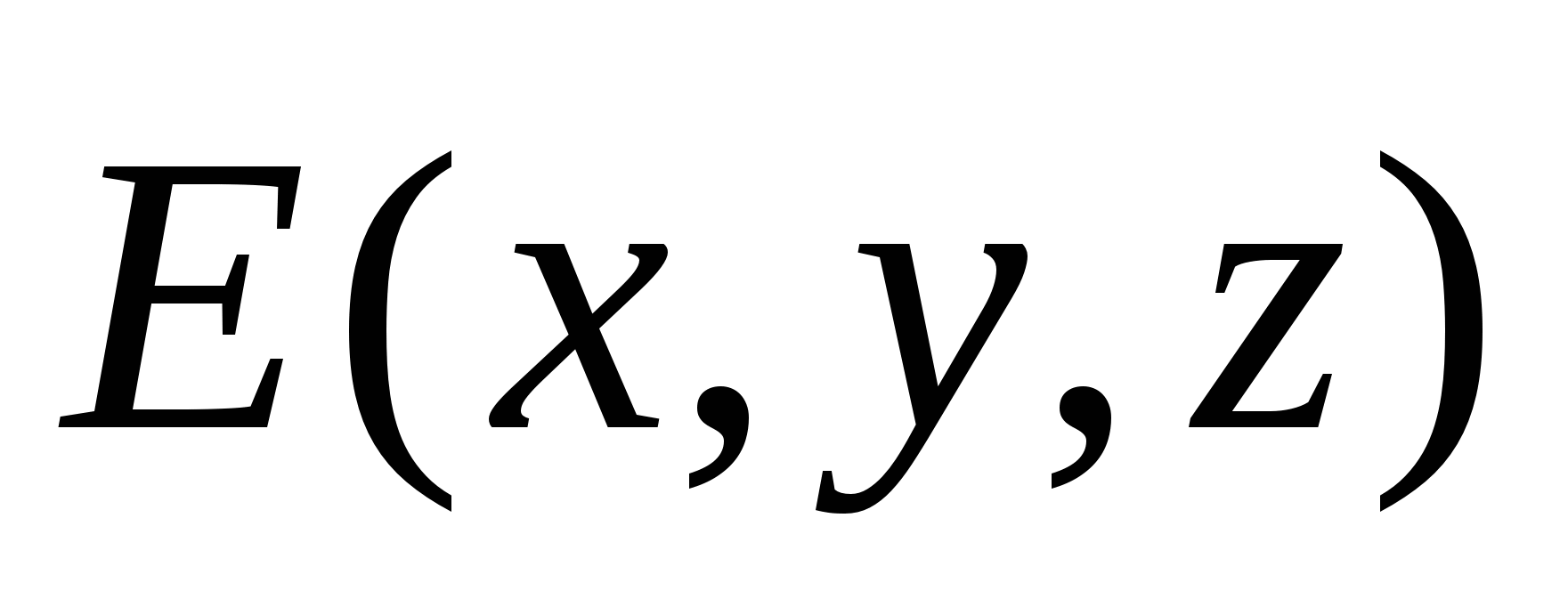 поля, т.е. решить прямую задачу электростатики.
поля, т.е. решить прямую задачу электростатики.
3.7. Вычисление разности потенциалов по напряженности поля простейших электростатических полей
Установленная связь между напряженностью и потенциалом позволяет по известной напряженности поля найти разность потенциалов между двумя произвольными точками этого поля.
Рассмотрим несколько примеров вычисления разности потенциалов между точками поля, созданного некоторыми заряженными телами.
1. Поле равномерно заряженной бесконечной плоскости
Поле равномерно заряженной бесконечной плоскости, найденная с помощью теоремы Остроградского-Гаусса, определяется по формуле  , где σ – поверхностная плотность заряда. Разность потенциалов между точками, лежащими на расстояниях x
1
и
x
2
от плоскости, равна
, где σ – поверхностная плотность заряда. Разность потенциалов между точками, лежащими на расстояниях x
1
и
x
2
от плоскости, равна ![]() .
.
- d
Е
= 0, между обкладками потенциал уменьшается по логарифмическому закону, а вторая обкладка (вне цилиндров) экранирует электрическое поле и φ и Е
равны нулю.

Рисунок 3.10
На рис. 3.10 изображена зависимость напряженности E и потенциала
 от r
.
от r
.4. Поле равномерно заряженной сферической поверхности
Рассматривая примеры применения теоремы Остроградского-Гаусса мы нашли, что напряженность поля сферы определяется формулой:
 (рис. 3.11). А т.к.
(рис. 3.11). А т.к.  , то
, то
Рисунок 3.11
. Если принять r 1 = r , а r 2 =∞, то потенциал вне сферической поверхности определяется выражением), определяется формулой
Счетом выбора нулевого уровня потенциала в точке r 2 =∞ потенциал любой точки внутри заряженного шара можно найти следующим образом: . После интегрирования, получим
. После интегрирования, получим  .
. 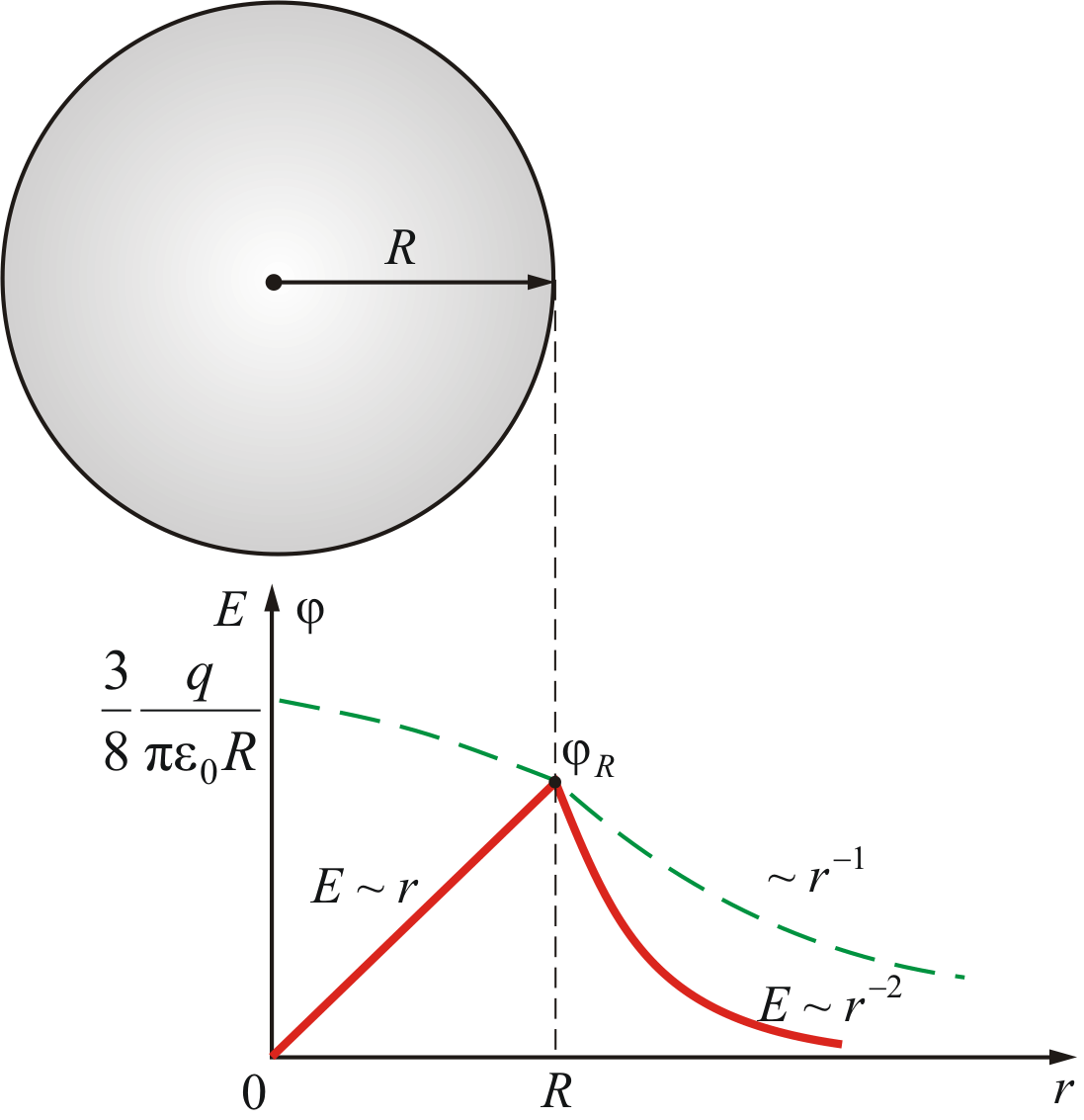
Рисунок 3.12
Если учесть, что
 , то
, то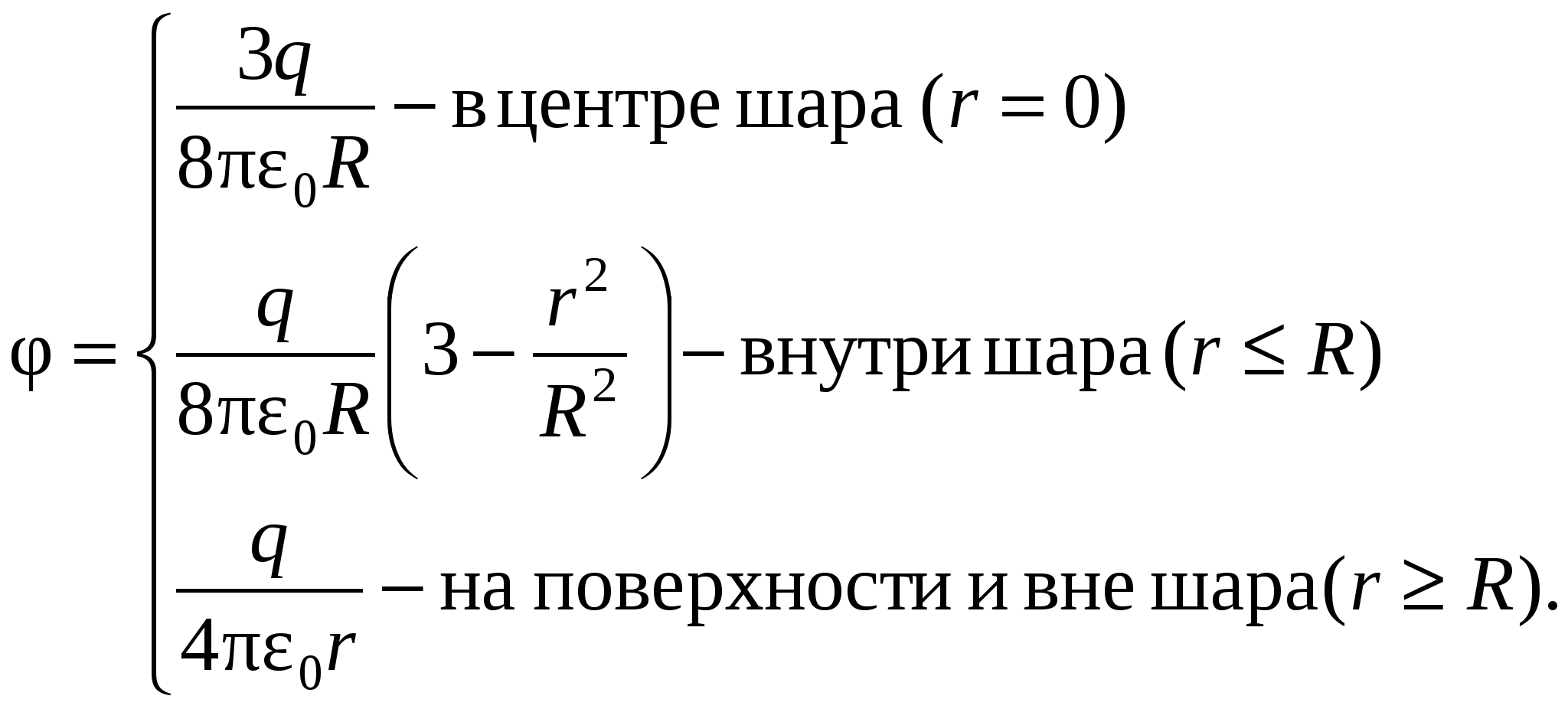 (38
)
(38
)
Из полученных соотношений можно сделать следующие выводы .
С помощью теоремы Гаусса сравнительно просто можно рассчитать Е и φ от различных заряженных поверхностей.
Напряженность поля в вакууме изменяется скачком при переходе через заряженную поверхность.
Потенциал поля – всегда непрерывная функция координат.
Контрольные вопросы
Как показать, что электростатическое поле потенциально?
Что такое потенциал?
Что называется циркуляцией вектора напряженности?
Какова связь напряженности и потенциала? Как по картине эквипотенциальных поверхностей нарисовать картину силовых линий поля?
Чему равна работа по перемещению заряда по эквипотенциальной поверхности?
Приведите примеры расчета разности потенциалов простейших электростатических полей.
Как ведет себя диполь во внешнем электростатическом поле?