3.1. Ekuacionet kanonike të drejtëzës.

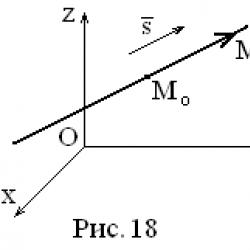
Le të jepet një vijë e drejtë në sistemin koordinativ Oxyz që kalon nëpër pikë

(shih Fig. 18) Le të shënojmë me
një vektor paralel me një vijë të caktuar. Vektor thirrur vektori drejtues i një drejtëze. Le të marrim një pikë në një vijë të drejtë
dhe merrni parasysh vektorët vektorë
janë kolineare, prandaj koordinatat e tyre përkatëse janë proporcionale:

(3.3.1 )

Këto ekuacione quhen ekuacionet kanonike drejt.

Shembull: Shkruani ekuacionet e drejtëzës që kalon në pikën M(1, 2, –1) paralele me vektorin

Zgjidhja: Vektor është vektori i drejtimit të vijës së dëshiruar. Duke zbatuar formulat (3.1.1), marrim:

Këto janë ekuacionet kanonike të vijës.

Koment: Kthimi në zero i njërit prej emërtuesve nënkupton kthimin në zero të numëruesit përkatës, pra y – 2 = 0; y = 2. Kjo drejtëz shtrihet në rrafshin y = 2, paralel me rrafshin Oxz.

3.2. Ekuacionet parametrike të një drejtëze.

Drejtëza le të jepet nga ekuacionet kanonike

Le të shënojmë
Pastaj
Vlera t quhet parametër dhe mund të marrë çdo vlerë:
.

Le të shprehim x, y dhe z në terma t:

(3.2.1 )

Ekuacionet që rezultojnë quhen ekuacionet parametrike të një drejtëze.

Shembulli 1: Përbërja e ekuacioneve parametrike të një drejtëze që kalon nëpër pikën M (1, 2, -1) paralele me vektorin

Zgjidhja: Ekuacionet kanonike të kësaj rreshti janë marrë në shembullin e paragrafit 3.1:

Për të gjetur ekuacionet parametrike të një drejtëze, zbatojmë derivimin e formulave (3.2.1):

Kështu që,
- ekuacionet parametrike të një drejtëze të caktuar.

Përgjigju:

Shembulli 2. Shkruani ekuacionet parametrike për një drejtëz që kalon nëpër pikën M (–1, 0, 1) paralel me vektorin
ku A (2, 1, –1), B (–1, 3, 2).

Zgjidhja: Vektor
është vektori i drejtimit të vijës së dëshiruar.

Le të gjejmë vektorin
.

= (–3; 2; 3). Duke përdorur formulat (3.2.1), shkruajmë ekuacionet e drejtëzës:

janë ekuacionet parametrike të kërkuara të drejtëzës.

3.3. Ekuacionet e një drejtëze që kalon nëpër dy pika të dhëna.

Një vijë e vetme e drejtë kalon nëpër dy pika të dhëna në hapësirë ​​(shih Fig. 20). Le të jepen pikët.Vektor
mund të merret si vektor i drejtimit të kësaj linje. Atëherë ekuacionet mund të gjenden drejtpërdrejt ato sipas formulave (3.1.1):
).

(3.3.1)

Shembulli 1. Hartoni ekuacione kanonike dhe parametrike të drejtëzës që kalon nëpër pika

Zgjidhje: Ne aplikojmë formulën (3.3.1)

Ne morëm ekuacionet kanonike të drejtëzës. Për të marrë ekuacione parametrike, zbatojmë derivimin e formulave (3.2.1). marrim

janë ekuacione parametrike të një drejtëze.

Shembulli 2. Hartoni ekuacione kanonike dhe parametrike të drejtëzës që kalon nëpër pika

Zgjidhje: Duke përdorur formulat (3.3.1) marrim:

Këto janë ekuacione kanonike.

Le të kalojmë te ekuacionet parametrike:

- ekuacionet parametrike.

Vija e drejtë që rezulton është paralele me boshtin oz (shih Fig. 21).

Le të jepen dy plane në hapësirë

Nëse këto plane nuk përkojnë dhe nuk janë paralele, atëherë ato kryqëzohen në një vijë të drejtë:

Ky sistem i dy ekuacioneve lineare përcakton një vijë të drejtë si vijën e kryqëzimit të dy planeve. Nga ekuacionet (3.4.1) mund të kalohet në ekuacionet kanonike (3.1.1) ose ekuacionet parametrike (3.2.1). Për ta bërë këtë, ju duhet të gjeni një pikë
shtrirë në një vijë të drejtë, dhe vektori i drejtimit Koordinatat e pikave
marrim nga sistemi (3.4.1), duke i dhënë njërës prej koordinatave një vlerë arbitrare (për shembull, z = 0). Pas vektorit udhëzues ju mund të merrni produktin vektorial të vektorëve, d.m.th

Shembulli 1. Hartoni ekuacionet kanonike të drejtëzës

Zgjidhja: Le të z = 0. Le të zgjidhim sistemin

Duke shtuar këto ekuacione, marrim: 3x + 6 = 0
x = –2. Zëvendësoni vlerën e gjetur x = –2 në ekuacionin e parë të sistemit dhe merrni: –2 + y + 1 = 0
y = 1.

Pra, periudha
shtrihet në vijën e dëshiruar.

Për të gjetur vektorin e drejtimit të një vije të drejtë, shkruajmë vektorët normalë të rrafsheve: dhe gjejmë produktin e vektorit të tyre:

Ne gjejmë ekuacionet e drejtëzës duke përdorur formulat (3.1.1):

Përgjigje:
.

Menyre tjeter: Ekuacionet kanonike dhe parametrike të drejtëzës (3.4.1) mund të merren lehtësisht duke gjetur dy pika të ndryshme në vijë nga sistemi (3.4.1), dhe më pas duke aplikuar formulat (3.3.1) dhe nxjerrjen e formulave (3.2. .1).

Shembulli 2. Të hartojë ekuacione kanonike dhe parametrike të drejtëzës

Zgjidhja: Le të jetë y = 0. Atëherë sistemi do të marrë formën:

Duke mbledhur ekuacionet, marrim: 2x + 4 = 0; x = –2. Zëvendësoni x = –2 në ekuacionin e dytë të sistemit dhe merrni: –2 –z +1 = 0
z = –1. Pra, e gjetëm pikën

Për të gjetur pikën e dytë, le të vendosim x = 0. Do të kemi:

Kjo eshte

Ne morëm ekuacionet kanonike të drejtëzës.

Le të hartojmë ekuacionet parametrike të drejtëzës:

Përgjigju:
;
.

3.5. Pozicioni relativ i dy vijave në hapësirë.

Lëreni drejt
jepen nga ekuacionet:

:
;
:

.

Këndi ndërmjet këtyre vijave kuptohet si kënd ndërmjet vektorëve të drejtimit të tyre (shih Fig. 22). Ky kënd gjejmë duke përdorur një formulë nga algjebra vektoriale:
ose

(3.5.1)

Nëse drejt
pingul (
), atë
Prandaj,

Ky është kushti i pingulitetit të dy drejtëzave në hapësirë.

Nëse drejt
paralele (
), atëherë vektorët e tyre të drejtimit janë kolinear (
), kjo eshte

(3.5.3 )

Ky është kushti i paralelizmit të dy drejtëzave në hapësirë.

Shembulli 1. Gjeni këndin midis vijave të drejta:

A).
Dhe

b).
Dhe

Zgjidhja: A). Le të shkruajmë vektorin e drejtimit të drejtëzës
Le të gjejmë vektorin e drejtimit
plane të përfshira në sistem Më pas gjejmë produktin e tyre vektor:

(shih shembullin 1 të pikës 3.4).

Duke përdorur formulën (3.5.1) marrim:

Prandaj,

b). Le të shkruajmë vektorët e drejtimit të këtyre drejtëzave: Vektorët
janë kolineare sepse koordinatat e tyre përkatëse janë proporcionale:

Pra është e drejtë
paralele (
), kjo eshte

Përgjigje: A).
b).

Shembulli 2. Vërtetoni pingulitetin e drejtëzave:

Dhe

Zgjidhja: Le të shkruajmë vektorin e drejtimit të drejtëzës së parë

Le të gjejmë vektorin e drejtimit vijë e dytë e drejtë. Për ta bërë këtë, ne gjejmë vektorë normalë
planet e përfshira në sistem: Le të llogarisim produktin e tyre vektor:

(Shih shembullin 1 të paragrafit 3.4).

Le të zbatojmë kushtin e pingulitetit të drejtëzave (3.5.2):

Kushti plotësohet; prandaj, vijat janë pingule (
).

Si të shkruani ekuacionet e një drejtëze në hapësirë?

Ekuacionet e një drejtëze në hapësirë

Ngjashëm me një vijë "të sheshtë", ka disa mënyra në të cilat ne mund të përcaktojmë një vijë në hapësirë. Le të fillojmë me kanonet - pika dhe vektori drejtues i rreshtit:

Nëse dihet një pikë e caktuar në hapësirë ​​që i përket një linje dhe vektori i drejtimit të kësaj linje, atëherë ekuacionet kanonike të kësaj linje shprehen me formulat:

Shënimi i mësipërm supozon se koordinatat e vektorit të drejtimit jo e barabartë me zero. Do të shohim se çfarë të bëjmë nëse një ose dy koordinata janë zero pak më vonë.

Njësoj si në artikull Ekuacioni i planit, për thjeshtësi do të supozojmë se në të gjitha problematikat e orës së mësimit veprimet kryhen në një bazë hapësire ortonore.

Shembulli 1

Hartoni ekuacionet kanonike të një drejtëze të dhënë një pikë dhe një vektor drejtimi

Zgjidhje: Ne hartojmë ekuacionet kanonike të rreshtit duke përdorur formulën:

Përgjigju:

Dhe është pa tru... edhe pse, jo, është fare pa tru.

Çfarë duhet të keni parasysh për këtë shembull shumë të thjeshtë? Së pari, ekuacionet që rezultojnë NUK kanë nevojë të zvogëlohen me një: . Për të qenë më të saktë, është e mundur që të shkurtohet, por në mënyrë të pazakontë dëmton syrin dhe krijon bezdi gjatë zgjidhjes së problemeve.

Dhe së dyti, në gjeometrinë analitike dy gjëra janë të pashmangshme - verifikimi dhe testimi:

Për çdo rast, ne shikojmë emëruesit e ekuacioneve dhe kontrollojmë - A është mirë aty shkruhen koordinatat e vektorit të drejtimit. Jo, mos e mendoni, ne nuk po bëjmë mësim në kopshtin Brake. Kjo këshillë është shumë e rëndësishme sepse ju lejon të eliminoni plotësisht gabimet e paqëllimshme. Askush nuk është i siguruar, po nëse e kanë kopjuar gabim? Do t'i jepet Çmimi Darvin në Gjeometri.

Janë marrë barazitë e sakta, që do të thotë se koordinatat e pikës plotësojnë ekuacionet tona, dhe vetë pika i përket me të vërtetë kësaj linje.

Testi është shumë i lehtë (dhe i shpejtë!) për t'u kryer nga goja.

Në një numër problemesh kërkohet të gjendet një pikë tjetër që i përket një linje të caktuar. Si ta bëjmë atë?

Marrim ekuacionet që rezultojnë dhe mendërisht "prisni", për shembull, pjesën e majtë: . Tani le ta barazojmë këtë pjesë në çdo numër(mos harroni se tashmë kishte një zero), për shembull, në një: . Meqenëse , atëherë dy "copat" e tjera gjithashtu duhet të jenë të barabarta me një. Në thelb, ju duhet të zgjidhni sistemin:

Le të kontrollojmë nëse pika e gjetur i plotëson ekuacionet :

Janë marrë barazitë e sakta, që do të thotë se pika qëndron vërtetë në vijën e dhënë.

Le të bëjmë vizatimin në një sistem koordinativ drejtkëndor. Në të njëjtën kohë, le të kujtojmë se si të përshkruajmë saktë pikat në hapësirë:

Le të ndërtojmë një pikë:
– nga origjina e koordinatave në drejtim negativ të boshtit vizatojmë një segment të koordinatës së parë (vijë e gjelbër me pika);
- koordinata e dytë është zero, kështu që ne nuk "dridhemi" nga boshti as në të majtë as në të djathtë;
– në përputhje me koordinatën e tretë, matni tre njësi lart (vija e purpurt me pika).

Ndërtoni një pikë: matni dy njësi "drejt jush" (vijë me pika të verdhë), një njësi në të djathtë (vijë me pika blu) dhe dy njësi poshtë (vijë me pika kafe). Vija me pika kafe dhe vetë pika janë të mbivendosura në boshtin koordinativ, vini re se ato janë në gjysmëhapësirën e poshtme dhe PARA të boshtit.

Vetë vija e drejtë kalon mbi bosht dhe, nëse syri im nuk më dështon, mbi bosht. Nuk dështon, u binda analitikisht. Nëse vija e drejtë kalonte PRAPA boshtit, atëherë duhet të fshini me gomë një pjesë të vijës sipër dhe poshtë pikës së kalimit.

Një vijë e drejtë ka një numër të pafund të vektorëve të drejtimit, për shembull:
(shigjeta e kuqe)

Rezultati ishte pikërisht vektori origjinal, por ky ishte thjesht një aksident, kështu zgjodha pikën. Të gjithë vektorët e drejtimit të një vije të drejtë janë kolinearë dhe koordinatat e tyre përkatëse janë proporcionale (për më shumë detaje, shih Varësia lineare (jo) e vektorëve. Baza e vektorëve). Pra, vektorët do të jenë edhe vektorë të drejtimit të kësaj linje.

Informacione shtesë për krijimin e vizatimeve tredimensionale në letër me kuadrate mund të gjenden në fillim të manualit Grafikët dhe vetitë e funksioneve. Në një fletore, shtigjet me pika me shumë ngjyra (shih vizatimin) zakonisht vizatohen hollë me një laps të thjeshtë duke përdorur të njëjtën vijë me pika.

Të merremi me raste të veçanta kur një ose dy koordinata të vektorit të drejtimit janë zero. Në të njëjtën kohë vazhdojmë edhe trajnimin e vizionit hapësinor, i cili ka filluar në fillim të orës së mësimit. Ekuacioni i planit. Dhe përsëri do t'ju tregoj përrallën e mbretit të zhveshur - do të vizatoj një sistem koordinativ bosh dhe do t'ju bind se ka linja hapësinore atje =)

Është më e lehtë të renditësh të gjashtë rastet:

1) Për një pikë dhe një vektor drejtimi, ekuacionet kanonike të drejtëzës ndahen në tre individual ekuacionet: .

Ose shkurt:

Shembulli 2: le të krijojmë ekuacione të një drejtëze duke përdorur një pikë dhe një vektor drejtimi:

Çfarë lloj linje është kjo? Vektori i drejtimit të drejtëzës është kolinear me vektorin njësi, që do të thotë se kjo drejtëz do të jetë paralele me boshtin. Ekuacionet kanonike duhet të kuptohen si më poshtë:
a) - "y" dhe "z" të përhershme, janë të barabarta numra specifikë;
b) ndryshorja “x” mund të marrë çdo vlerë: (në praktikë, ky ekuacion zakonisht nuk shkruhet).

Në veçanti, ekuacionet përcaktojnë vetë boshtin. Në të vërtetë, "x" merr çdo vlerë, dhe "y" dhe "z" janë gjithmonë të barabarta me zero.

Ekuacionet në shqyrtim mund të interpretohen në një mënyrë tjetër: le të shohim, për shembull, shënimin analitik të boshtit të abshisë: . Në fund të fundit, këto janë ekuacione të dy planeve! Ekuacioni specifikon rrafshin koordinativ, dhe ekuacioni specifikon planin koordinativ. Ju mendoni saktë - këto plane koordinative kryqëzohen përgjatë boshtit. Ne do të shqyrtojmë metodën kur një vijë e drejtë në hapësirë ​​përcaktohet nga kryqëzimi i dy planeve në fund të mësimit.

Dy raste të ngjashme:

2) Ekuacionet kanonike të drejtëzës që kalon në një pikë paralele me vektorin shprehen me formula.

Vija të tilla të drejta do të jenë paralele me boshtin koordinativ. Në veçanti, ekuacionet specifikojnë vetë boshtin koordinativ.

3) Ekuacionet kanonike të drejtëzës që kalon në një pikë paralele me vektorin shprehen me formula.

Këto vija të drejta janë paralele me boshtin koordinativ dhe ekuacionet përcaktojnë vetë boshtin e aplikuar.

Le t'i vendosim tre të dytat në tezgë:

4) Për një vektor të pikës dhe një drejtimi, ekuacionet kanonike të drejtëzës zbërthehen në proporcion dhe ekuacioni i rrafshët .

Shembulli 3: le të hartojmë ekuacionet e një drejtëze duke përdorur një pikë dhe një vektor drejtimi.

Le l- një vijë e drejtë hapësire. Si në planimetri, çdo vektor

A =/= 0, vijë kolineare l, thirri vektor udhëzues këtë vijë të drejtë.

Pozicioni i vijës në hapësirë ​​përcaktohet plotësisht duke specifikuar vektorin e drejtimit dhe pikën që i përket vijës.

Le të jetë e drejtë l me vektor udhëzues A kalon nëpër pikën M 0, dhe M është një pikë arbitrare në hapësirë. Natyrisht, pika M (Fig. 197) i përket vijës l nëse dhe vetëm nëse vektori \(\overrightarrow(M_0 M)\) është në linjë me vektorin A , d.m.th.

\(\shigjeta mbi të djathtë(M_0 M)\) = t a , t\(\në\) R. (1)

Nëse pikat M dhe M 0 përcaktohen nga vektorët e rrezes së tyre r Dhe r 0 (Fig. 198) në lidhje me një pikë O në hapësirë, atëherë \(\overrightarrow(M_0 M)\) = r - r 0 , dhe ekuacioni (1) merr formën

r = r 0 + t a , t\(\në\) R. (2)

Quhen ekuacionet (1) dhe (2). ekuacionet vektoro-parametrike të një drejtëze. E ndryshueshme t në ekuacionet vektoro-parametrike quhet drejtëza parametri.

Le të jetë pika M 0 drejtëz l dhe vektori i drejtimit a jepen nga koordinatat e tyre:

M 0 ( X 0 ; në 0 , z 0), A = (A 1 ; A 2 ; A 3).

Atëherë nëse ( X; y; z) - koordinatat e një pike arbitrare M të një drejtëze l, Kjo

\(\arrow overright (M_0 M) \) = ( x - x 0 ; y - y 0 ; z - z 0)

dhe ekuacioni vektorial (1) është i barabartë me tre ekuacionet e mëposhtme:

x - x 0 = ta 1 , y - y 0 = ta 2 , z - z 0 = ta 3

$$ \fillimi(rastet) x = x_0 + ta_1 \\ y = y_0 + ta_2 \\ z = z_0 + ta_3, \;\;t\në R\end (rastet) (3)$$

Quhen ekuacionet (3). ekuacionet parametrike të drejtëzës në hapësirë.

Detyra 1. Shkruani ekuacionet parametrike për një drejtëz që kalon nga një pikë

M 0 (-3; 2; 4) dhe ka një vektor drejtimi A = (2; -5; 3).

Në këtë rast X 0 = -3, në 0 = 2, z 0 = 4; A 1 = 2; A 2 = -5; A 3 = 3. Duke zëvendësuar këto vlera në formula (3), marrim ekuacionet parametrike të kësaj linje

$$ \fillimi(rastet) x = -3 - 2t \\ y = 2 - 5t \\ z = 4 + 3t, ​​\;\;t\në R\end (rastet) $$

Le të përjashtojmë parametrin t nga ekuacionet (3). Kjo mund të bëhet sepse A =/= 0, dhe për këtë arsye një nga koordinatat vektoriale A është padyshim i ndryshëm nga zero.

Le të jenë së pari të gjitha koordinatat të ndryshme nga zero. Pastaj

$$ t=\frac(x-x_0)(a_1),\;\;t=\frac(y-y_0)(a_2),\;\;t=\frac(z-z_0)(a_3) $$

dhe për këtë arsye

$$ \frac(x-x_0)(a_1)=\frac(y-y_0)(a_2)=\frac(z-z_0)(a_3) \;\; (4)$$

Këto ekuacione quhen ekuacionet kanonike të drejtëzës .

Vini re se ekuacionet (4) formojnë një sistem prej dy ekuacionesh me tre ndryshore x, y Dhe z.

Nëse në ekuacionet (3) njëra nga koordinatat vektoriale A , Për shembull A 1 është e barabartë me zero, pastaj duke eliminuar parametrin t, përsëri marrim një sistem prej dy ekuacionesh me tre ndryshore x, y Dhe z:

\(x=x_0, \;\; \frac(y-y_0)(a_2)=\frac(z-z_0)(a_3)\)

Këto ekuacione quhen edhe ekuacione të vijës kanonike. Për uniformitet, ato gjithashtu shkruhen në mënyrë konvencionale në formën (4)

\(\frac(x-x_0)(0)=\frac(y-y_0)(a_2)=\frac(z-z_0)(a_3)\)

duke supozuar se nëse emëruesi është zero, atëherë edhe numëruesi përkatës është zero. Këto ekuacione janë ekuacionet e një drejtëze që kalon nëpër pikën M 0 ( X 0 ; në 0 , z 0) paralel me planin koordinativ yOz, meqenëse vektori i drejtimit të tij (0; A 2 ; A 3).

Së fundi, nëse në ekuacionet (3) ka dy koordinata vektoriale A , Për shembull A 1 dhe A 2 janë të barabarta me zero, atëherë këto ekuacione marrin formën

X = X 0 , y = në 0 , z = z 0 + t a 3 , t\(\në\) R.

Këto janë ekuacionet e një drejtëze që kalon nëpër pikën M 0 ( X 0 ; në 0 ; z 0) paralel me boshtin Oz. Për një vijë kaq të drejtë X = X 0 , y = në 0, a z- çdo numër. Dhe në këtë rast, për uniformitet, ekuacioni i drejtëzës mund të shkruhet (me të njëjtën rezervë) në formën (4)

\(\frac(x-x_0)(0)=\frac(y-y_0)(0)=\frac(z-z_0)(a_3)\)

Kështu, për çdo rresht në hapësirë ​​mund të shkruhet ekuacione kanonike (4), dhe anasjelltas, çdo ekuacion i formës (4) me kusht që të paktën një nga koeficientët A 1 , A 2 , A 3 nuk është e barabartë me zero, përcakton një vijë të drejtë në hapësirë.

Detyra 2. Shkruani ekuacionet kanonike të një drejtëze që kalon nëpër pikën M 0 (- 1; 1, 7) paralel me vektorin A = (1; 2; 3).

Ekuacionet (4) në këtë rast shkruhen si më poshtë:

\(\frac(x+1)(1)=\frac(y-1)(2)=\frac(z-7)(3)\)

Le të nxjerrim ekuacionet e një drejtëze që kalon nëpër dy pika të dhëna M 1 ( X 1 ; në 1 ; z 1) dhe

M2( X 2 ; në 2 ; z 2). Natyrisht, ne mund të marrim vektorin a = (X 2 - X 1 ; në 2 - në 1 ; z 2 - z 1), dhe përtej pikës M 0 përmes së cilës kalon një vijë e drejtë, për shembull, pika M 1. Atëherë ekuacionet (4) do të shkruhen si më poshtë:

\(\frac(x-x_1)(x_2 - x_1)=\frac(y-y_1)(y_2 - y_1)=\frac(z-z_1)(z_2 - z_1)\) (5)

Këto janë ekuacionet e një drejtëze që kalon nëpër dy pika M 1 ( X 1 ; në 1 ; z 1) dhe

M2( X 2 ; në 2 ;z 2).

Detyra 3. Shkruani ekuacionet e një drejtëze që kalon nëpër pikat M 1 (-4; 1; -3) dhe M 2 (-5; 0; 3).

Në këtë rast X 1 = -4, në 1 = 1, z 1 = -3, X 2 = -5, në 2 = 0, z 2 = 3. Duke i zëvendësuar këto vlera në formula (5), marrim

\(\frac(x+4)(-1)=\frac(y-1)(-1)=\frac(z+3)(6)\)

Detyra 4. Shkruani ekuacionet e drejtëzës që kalon nëpër pikat M 1 (3; -2; 1) dhe

M 2 (5; -2; 1/2).

Pas zëvendësimit të koordinatave të pikave M 1 dhe M 2 në ekuacionet (5), marrim

\(\frac(x-3)(2)=\frac(y+2)(0)=\frac(z-1)(-\frac(1)(2))\)

Ekuacionet kanonike të drejtëzës

Formulimi i problemit. Gjeni ekuacionet kanonike të drejtëzës së dhënë si drejtëza e prerjes së dy rrafsheve (ekuacionet e përgjithshme)

Plani i zgjidhjes. Ekuacionet kanonike të një drejtëze me një vektor drejtimi duke kaluar nëpër një pikë të caktuar , kanë formën

. (1)

Prandaj, për të shkruar ekuacionet kanonike të një drejtëze, është e nevojshme të gjendet vektori i drejtimit të saj dhe një pikë në vijë.

1. Meqenëse drejtëza u përket të dy planeve njëkohësisht, vektori i drejtimit të saj është ortogonal me vektorët normalë të të dy rrafsheve, d.m.th. sipas përkufizimit të produktit vektor, kemi

. (2)

2. Zgjidhni një pikë në vijë. Meqenëse vektori i drejtimit të drejtëzës nuk është paralel me të paktën njërin prej rrafsheve koordinative, drejtëza e pret këtë plan koordinativ. Rrjedhimisht, pika e kryqëzimit të saj me këtë plan koordinativ mund të merret si një pikë në një vijë.

3. Zëvendësoni koordinatat e gjetura të vektorit udhëzues dhe drejtojeni në ekuacionet kanonike të drejtëzës (1).

Koment. Nëse prodhimi vektorial (2) është i barabartë me zero, atëherë rrafshet nuk priten (paralele) dhe nuk është e mundur të shkruhen ekuacionet kanonike të drejtëzës.

Problemi 12. Shkruani ekuacionet kanonike të drejtëzës.

Ekuacionet kanonike të drejtëzës:

,

Ku - koordinatat e çdo pike në një vijë, është vektori i drejtimit të tij.

Le të gjejmë një pikë në vijë. Le të jetë atëherë

Prandaj, – koordinatat e një pike që i përket një drejtëze.

Le të shohim shembullin e zgjidhjes.

Shembull.

Gjeni koordinatat e çdo pike në një drejtëz të përcaktuar në hapësirë ​​nga ekuacionet e dy rrafsheve të kryqëzuara .

Zgjidhje.

Le ta rishkruajmë sistemin e ekuacioneve në formën e mëposhtme

Si bazë minore e matricës kryesore të sistemit, marrim një minor jo zero të rendit të dytë , domethënë z është një variabël i panjohur i lirë. Le t'i zhvendosim termat që përmbajnë z në anët e djathta të ekuacioneve: .

Le të pranojmë , ku është një numër real arbitrar, atëherë .

Le të zgjidhim sistemin e ekuacioneve që rezulton:

Kështu, zgjidhja e përgjithshme e sistemit të ekuacioneve ka formën , ku .

Nëse marrim një vlerë specifike të parametrit, atëherë marrim një zgjidhje të veçantë për sistemin e ekuacioneve, i cili na jep koordinatat e dëshiruara të një pike që shtrihet në një vijë të caktuar. Le ta marrim atëherë , pra, është pika e dëshiruar e vijës.

Ju mund të kontrolloni koordinatat e gjetura të një pike duke i zëvendësuar ato në ekuacionet origjinale të dy planeve të kryqëzuara:

Përgjigje:

Vektori i drejtimit të drejtëzës përgjatë së cilës kryqëzohen dy rrafshe.

Në një sistem koordinativ drejtkëndor, vektori drejtues i drejtëzës është i pandashëm nga një vijë e drejtë. Kur drejtëza a në një sistem koordinativ drejtkëndor në hapësirën tredimensionale jepet nga ekuacionet e dy rrafsheve të kryqëzuara dhe , atëherë koordinatat e vektorit drejtues të drejtëzës nuk janë të dukshme. Tani do të tregojmë se si t'i përcaktojmë ato.

Ne e dimë se një drejtëz është pingul me një rrafsh kur është pingul me çdo drejtëz që shtrihet në atë rrafsh. Atëherë vektori normal i një rrafshi është pingul me çdo vektor jozero që shtrihet në këtë plan. Ne do t'i përdorim këto fakte për të gjetur vektorin e drejtimit të vijës.

Vija e drejtë a shtrihet si në rrafsh ashtu edhe në rrafsh. Prandaj, vektori i drejtimit të drejtëzës a është pingul me vektorin normal plan, dhe vektor normal aeroplan Kështu, vektori i drejtimit të drejtëzës a është Dhe :

Bashkësia e të gjithë vektorëve të drejtimit të një vije të drejtë dhe ne mund ta përcaktojmë atë si , ku është një parametër që mund të marrë çdo vlerë reale përveç zeros.

Shembull.

Gjeni koordinatat e çdo vektori të drejtimit të një vije të drejtë, e cila specifikohet në sistemin e koordinatave drejtkëndore Oxyz në hapësirën tredimensionale nga ekuacionet e dy rrafsheve të kryqëzuara .

Zgjidhje.

Vektorët normalë të planeve janë vektorët Dhe përkatësisht. Vektori drejtues i një vije të drejtë, e cila është kryqëzimi i dy planeve të dhëna, është prodhimi vektorial i vektorëve normalë:

Përgjigje:

Kalimi në ekuacionet parametrike dhe kanonike të një vije të drejtë në hapësirë.

Ka raste në të cilat përdorimi i ekuacioneve të dy rrafsheve të kryqëzuara për të përshkruar një vijë të drejtë nuk është plotësisht i përshtatshëm. Disa probleme janë më të lehta për t'u zgjidhur nëse dihen ekuacionet kanonike të një vije të drejtë në hapësirë: ose ekuacionet parametrike të një drejtëze në hapësirën e formës , ku x 1 , y 1 , z 1 janë koordinatat e një pike të caktuar në vijë, a x , a y , a z janë koordinatat e vektorit drejtues të drejtëzës dhe është një parametër që merr vlera reale arbitrare. Le të përshkruajmë procesin e kalimit nga ekuacionet lineare të formës te ekuacionet kanonike dhe parametrike të një drejtëze në hapësirë.

Në paragrafët e mëparshëm, mësuam të gjejmë koordinatat e një pike të caktuar në një drejtëz, si dhe koordinatat e një vektori të caktuar drejtimi të një drejtëze, i cili jepet nga ekuacionet e dy rrafsheve të kryqëzuara. Këto të dhëna janë të mjaftueshme për të shkruar ekuacionet kanonike dhe parametrike të kësaj linje në një sistem koordinativ drejtkëndor në hapësirë.

Le të shqyrtojmë zgjidhjen e shembullit, dhe pas kësaj do të tregojmë një mënyrë tjetër për të gjetur ekuacionet kanonike dhe parametrike të një drejtëze në hapësirë.

Shembull.

Zgjidhje.

Le të llogarisim fillimisht koordinatat e vektorit drejtues të drejtëzës. Për ta bërë këtë, gjejmë produktin vektorial të vektorëve normalë Dhe aeroplanët Dhe :

Kjo eshte, .

Tani le të përcaktojmë koordinatat e një pike të caktuar në një vijë të caktuar. Për ta bërë këtë, ne do të gjejmë një nga zgjidhjet e sistemit të ekuacioneve .

Përcaktues është e ndryshme nga zero, le ta marrim si bazë minore të matricës kryesore të sistemit. Atëherë ndryshorja z është e lirë, ne transferojmë termat me të në anët e djathta të ekuacioneve dhe i japim ndryshores z një vlerë arbitrare:

Ne zgjidhim sistemin rezultues të ekuacioneve duke përdorur metodën Cramer:

Prandaj,

Ne pranojmë dhe marrim koordinatat e pikës në vijë: .

Tani mund të shkruajmë ekuacionet e kërkuara kanonike dhe parametrike të linjës origjinale në hapësirë:

Përgjigje:

Dhe

Këtu është mënyra e dytë për të zgjidhur këtë problem.

Kur gjejmë koordinatat e një pike të caktuar në një drejtëz, zgjidhim sistemin e ekuacioneve . Në përgjithësi, zgjidhjet e tij mund të shkruhen në formë .

Dhe këto janë pikërisht ekuacionet parametrike të kërkuara të një vije të drejtë në hapësirë. Nëse secili prej ekuacioneve rezultuese zgjidhet në lidhje me një parametër dhe pastaj barazohen anët e djathta të barazive, atëherë marrim ekuacionet kanonike të një vije të drejtë në hapësirë

Le të tregojmë zgjidhjen e problemit të mëparshëm duke përdorur këtë metodë.

Shembull.

Një vijë e drejtë në hapësirën tredimensionale përcaktohet nga ekuacionet e dy rrafsheve të kryqëzuara . Shkruani ekuacione kanonike dhe parametrike për këtë rresht.

Zgjidhje.

Këtë sistem prej dy ekuacionesh e zgjidhim me tre të panjohura (zgjidhja është dhënë në shembullin e mëparshëm, nuk do ta përsërisim). Në këtë rast marrim . Këto janë ekuacionet parametrike të dëshiruara të një vije të drejtë në hapësirë.

Mbetet për të marrë ekuacionet kanonike të një vije të drejtë në hapësirë:

Ekuacionet e vijës së drejtë që rezultojnë janë të ndryshme nga jashtë nga ekuacionet e marra në shembullin e mëparshëm, por ato janë ekuivalente, pasi ato përcaktojnë të njëjtin grup pikash në hapësirën tre-dimensionale (dhe për rrjedhojë të njëjtën vijë të drejtë).

Përgjigje:

Dhe

Bibliografi.

• Bugrov Ya.S., Nikolsky S.M. Matematikë e lartë. Vëllimi i parë: elemente të algjebrës lineare dhe gjeometrisë analitike.
• Ilyin V.A., Poznyak E.G. Gjeometria analitike.