1. Let's take a regular triangle.
2. We cut out a triangle from it, the vertices of which lie at the midpoints of the sides of the original one. As a result, we get three triangles on the plane, the area of ​​each of which is four times less than the area of ​​the original one.
3. We perform the previous manipulations with the resulting triangles.

The process looks like this:

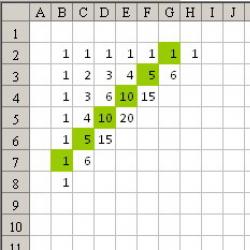
1. Interestingly, if in Pascal’s triangle all odd numbers are colored one color and even numbers another, then a Sierpinski triangle is formed.

Let's take advantage of this fact. Only in Excel it is more convenient to use not the classic (line-by-row) form of Pascal’s triangle, but this:

Here the binomial coefficients are written diagonally, in the first filled row and the first filled column of unity, and in the rest the sum of the top and left elements.

Let's move on to construction. For us it is enough to write down not the coefficients, but only their parity.

First, let's make the cells size in Excel, for example 7 by 7 pixels.

Let's stand in cell B2, then select the area B2:DY129 - to do this, press Ctrl + G and write B2:DY129 in the link field.

Now in the formula bar we write =IF(OR(ROW()=2,COLUMN()=2),1,REM(A2+B1,2))
and press Ctrl + Enter to fill the entire selected area with a similar formula.

Let's go Menu - Conditional Formatting and for value 1 we indicate the color of the cell.

As a result we get:

It should be noted that the Sierpinski triangle is obtained by some kind of random walk on the plane. Namely:

1. Let's fix 3 vertices of the triangle on the plane and take another point.
2. We obtain the first point as the midpoint of the segment between accidentally the selected vertex and point from step 1.
3. We obtain the second point as the midpoint of the segment between accidentally the selected vertex and the first point.
4. We repeat the process many times.

You can use this macro:

Public Sub Macro()

Dim arRange(1 To 3) As Range
Dim tekRow As Integer
Dim tekColumn As Integer
Dim i As Integer
Dim iT As Integer

tekRow = Int(1000 * Rnd) + 1
tekColumn = Int(200 * Rnd) + 1

Set arRange(1) = Cells(1, 1)
Set arRange(2) = Cells(50, 250)
Set arRange(3) = Cells(200, 20)

Cells.Clear

For i = 1 To 20000
iT = (Int(1000 * Rnd) Mod 3) + 1
tekRow = Int((tekRow + arRange(iT).Row) / 2)
tekColumn = Int((tekColumn + arRange(iT).Column) / 2)
Cells(tekRow, tekColumn).Interior.ColorIndex = 5
Next

End Sub

Sierpinski triangle- a fractal, one of the two-dimensional analogues of the Cantor set, proposed by the Polish mathematician Waclaw Sierpinski in 1915. Also known as Sierpinski's "napkin".

Sierpinski triangle

Construction

Iterative method

Construction of the Sierpinski triangle

The midpoints of the sides of an equilateral triangle are connected by segments. You get 4 new triangles. The interior of the middle triangle is removed from the original triangle. It turns out a lot T 1 (\displaystyle T_(1)), consisting of the 3 remaining “first rank” triangles. Doing exactly the same with each of the triangles of the first rank, we obtain the set T 2 (\displaystyle T_(2)), consisting of 9 equilateral triangles of the second rank. Continuing this process indefinitely, we get an infinite sequence T 0 ⊃ T 1 ⊃ ⋯ ⊃ T n ⊃ … (\displaystyle T_(0)\supset T_(1)\supset \dots \supset T_(n)\supset \dots ), the intersection of whose members is a Sierpinski triangle.

Chaos method

1. The coordinates of the attractors are specified - the vertices of the original triangle T 0 (\displaystyle T_(0)). 2. Probability space (0 ; 1) (\displaystyle (0;1)) is divided into 3 equal parts, each of which corresponds to one attractor. 3. A certain starting point is specified P 0 (\displaystyle P_(0)), lying inside the triangle T 0 (\displaystyle T_(0)). 4. Beginning of the cycle of constructing points belonging to the set of the Sierpinski triangle. 1. A random number is generated n ∈ (0 ; 1) (\displaystyle n\in (0;1)). 2. The active attractor becomes the vertex in whose probabilistic subspace the generated number fell. 3. A point is being constructed P i (\displaystyle P_(i)) with new coordinates: x i = x i − 1 + x A 2 ; y i = y i − 1 + y A 2 (\displaystyle x_(i)=(\frac (x_(i-1)+x_(A))(2));y_(i)=(\frac (y_(i -1)+y_(A))(2))), Where: x i − 1 , y i − 1 (\displaystyle x_(i-1),y_(i-1))- coordinates of the previous point P i − 1 (\displaystyle P_(i-1)); x A , y A (\displaystyle x_(A),y_(A))- coordinates of the active attractor point. 5. Return to the beginning of the cycle.

Properties

Construction by iterative method

Construction using the chaos method

Notes

Links

L-system

The L-system or Lindenmayer system is a parallel rewriting system and a type of formal grammar. The L-system consists of an alphabet of symbols that can be used to create strings, a set of generating rules that specify the rules for substitution for each symbol, an initial string (“axiom”) from which construction begins, and a mechanism for translating the generated string into geometric structures. L-systems were proposed and developed in 1968 by Aristide Lindenmayer, a Hungarian biologist and botanist at Utrecht University. Lindenmayer used L-systems to describe the behavior of plant cells and model the process of plant development. L-systems have also been used to model the morphology of various organisms and can be used to generate self-similar fractals such as iterable function systems.

Racket (programming language)

Racket (formerly PLTScheme) is a multi-paradigm general-purpose programming language belonging to the Lisp/Scheme family. Provides an environment for language-oriented programming - one of the purposes of racket is the creation, development and implementation of programming languages. The language is used in various contexts: as a scripting language, as a general-purpose language, in computer science teaching, in scientific research.

The platform provides the user with an implementation of the Racket language, including a developed run time system, various libraries, a JIT compiler, etc., as well as the DrRacket development environment (formerly known as DrScheme) written in Racket. This software framework is used in MIT's ProgramByDesign course. The core Racket language features a powerful macro system that allows you to create embedded and domain-specific programming languages, language constructs (for example, classes and modules) and Racket dialects with different semantics.

The system is free and open source software distributed under LGPL terms. Extensions and packages written by the community are available on PLaneT, the system's web distribution.

Fractal compression algorithm

Fractal image compression is a lossy image compression algorithm based on the application of systems of iterated functions (usually affine transformations) to images. This algorithm is known for the fact that in some cases it allows one to obtain very high compression ratios with acceptable visual quality for real photographs of natural objects. Due to the difficult situation with patenting, the algorithm was not widely used.

Dividing tile

Rep-tile is a mosaic geometry concept, a figure that can be cut into smaller copies of the figure itself. In 2012, a generalization of dividing tilings called self-tiling tile set was proposed by English mathematician Lee Salous in Mathematics Magazine.

Final subdivision rule

In mathematics, the ultimate rule of subdivision is a recursive way of dividing a polygon and other two-dimensional shapes into smaller and smaller pieces. Subdivision rules in this sense are a generalization of fractals. Instead of repeating the same pattern over and over again, there are subtle changes at each step, allowing for richer structures while still maintaining the elegant fractal style. Subdivision rules are used in architecture, biology and computer science, as well as in the study of hyperbolic manifolds. Tile substitutions are a well-studied type of subdivision rule.

Peano curve

Peano curve is a general name for parametric curves whose image contains a square (or, more generally, open regions of space). Another name is a space-filling curve.

Named after Giuseppe Peano (1858-1932), the discoverer of this kind of curve, the Peano curve is the name given to the specific curve that Peano found.

Sierpinski curve

Sierpinski curves is a recursively defined sequence of continuous closed planar fractal curves discovered by Waclaw Sierpinski. The curve in the limit at completely fills the unit square, so the limit curve, also called Sierpinski curve, is an example of space-filling curves.

Since the Sierpinski curve fills space, its Hausdorff dimension (in the limit at n → ∞ (\displaystyle n\rightarrow \infty )) is equal to 2 (\displaystyle 2).
Euclidean curve length

equal to l n = 2 3 (1 + 2) 2 n − 1 3 (2 − 2) 1 2 n (\displaystyle l_(n)=(2 \over 3)(1+(\sqrt (2)))2^( n)-(1 \over 3)(2-(\sqrt (2)))(1 \over 2^(n))),

i.e. it is growing exponentially By n (\displaystyle n), and the limit at n → ∞ (\displaystyle n\rightarrow \infty ) area of ​​the region enclosed by the curve S n (\displaystyle S_(n)), is 5/12 (\displaystyle 5/12) square (in the Euclidean metric).

Logarithm

Logarithm of a number b (\displaystyle b) based on a (\displaystyle a) (from ancient Greek. λόγος "word; attitude" + ἀριθμός "number") is defined as an indicator of the power to which the base must be raised a (\displaystyle a) to get the number b (\displaystyle b). Designation: log a ⁡ b (\displaystyle \log _(a)b), pronounced: " logarithm b (\displaystyle b) based on a (\displaystyle a) ».

From the definition it follows that finding x = log a ⁡ b (\displaystyle x=\log _(a)b) is equivalent to solving the equation a x = b (\displaystyle a^(x)=b). For example, log 2 ⁡ 8 = 3 (\displaystyle \log _(2)8=3), because 2 3 = 8 (\displaystyle 2^(3)=8).

Calculating the logarithm is called by logarithm. Numbers a , b (\displaystyle a,b) most often real, but there is also a theory of complex logarithms.

Logarithms have unique properties that have determined their widespread use to significantly simplify labor-intensive calculations. When moving “into the world of logarithms,” multiplication is replaced by a much simpler addition, division is replaced by subtraction, and exponentiation and root extraction are transformed, respectively, into multiplication and division by the exponent. Laplace said that the invention of logarithms, “by shortening the astronomer’s work, doubled his life.”

The definition of logarithms and a table of their values ​​(for trigonometric functions) was first published in 1614 by the Scottish mathematician John Napier. Logarithmic tables, expanded and refined by other mathematicians, were widely used for scientific and engineering calculations for more than three centuries, until the advent of electronic calculators and computers.

Over time, it became clear that the logarithmic function y = log a ⁡ x (\displaystyle y=\log _(a)x) is irreplaceable in many other areas of human activity: solving differential equations, classifying the values ​​of quantities (for example, frequency and intensity of sound), approximation of various dependencies, information theory, probability theory, etc. This function is one of the elementary ones, it is the inverse of to the exponential function. The most commonly used are real logarithms with bases 2 (\displaystyle 2)(binary), e (\displaystyle e) (natural logarithm) and 10 (\displaystyle 10)(decimal).

DNA-based nanotechnology

DNA nanotechnology is the development and production of artificial structures from nucleic acids for technological use. In this scientific field, nucleic acids are used not as carriers of genetic information in living cells, but as a material for the needs of non-biological engineering of nanomaterials.

The technology uses strict rules for base pairing of nucleic acids, which only allow parts of the strands with complementary base sequences to be linked together to form a strong, rigid double helix structure. From these rules, it becomes possible to engineer sequences of bases that will be selectively assembled to form complex target structures with precisely tuned nanoscale shapes and properties. Most materials are made using DNA, but structures incorporating other nucleic acids such as RNA and peptide nucleic acids (PNA) have also been built, allowing the technology field to be called "nucleotide base nanotechnology".

The basic concept of DNA-based nanotechnology was first proposed in the early 1980s by Nadrian Seaman, and this research field began to attract widespread interest in the mid-2000s. Researchers working in this emerging field of technology have created static structures such as two- and three-dimensional crystal lattices, nanotubes, polyhedra and other freeform shapes, as well as functional structures such as molecular machines and DNA computers.

A variety of techniques are used to assemble these structures, including tile structuring, where tiles are assembled from smaller structures, folding structures created using the DNA origami technique, and dynamically rearranged structures created using strand displacement techniques. The research field is beginning to be used as a tool for solving basic science problems in the fields of structural biology and biophysics, including applied problems of crystallography and spectroscopy for protein structure determination. Research is also underway for potential applications in scalable molecular electronics and nanomedicine.

Natural logarithm

Natural logarithm is the logarithm to the base e, Where e (\displaystyle e)- an irrational constant equal to approximately 2.72. It is denoted as ln ⁡ x (\displaystyle \ln x), log e ⁡ x (\displaystyle \log _(e)x) or sometimes just log ⁡ x (\displaystyle \log x), if the base e (\displaystyle e) implied. Usually the number x (\displaystyle x) under the sign of the logarithm is real, but this concept can be extended to complex numbers.

From the definition it follows that the logarithmic dependence is the inverse function for the exponential y = e x (\displaystyle y=e^(x)), therefore their graphs are symmetrical with respect to the bisector of the first and third quadrants (see the figure on the right). Like the exponential function, the logarithmic function belongs to the category of transcendental functions.

Natural logarithms are useful for solving algebraic equations in which the unknown is present as an exponent, and they are indispensable in mathematical analysis. For example, logarithms are used to find the decay constant for a known half-life or to find the decay time in solving radioactivity problems. They play an important role in many areas of mathematics and applied sciences, and are used in finance to solve many problems, including finding compound interest.

Lebesgue dimension

Lebesgue dimension or topological dimension- dimension defined by coverings, the most important invariant of topological space. Lebesgue dimension of space X (\displaystyle X) usually denoted dim ⁡ X (\displaystyle \dim X).

Recursion

Recursion is a definition, description, image of an object or process within this object or process itself, that is, a situation when an object is part of itself. The term “recursion” is used in various specialized fields of knowledge - from linguistics to logic, but is most widely used in mathematics and computer science.

Sierpinski, Waclaw

Wacław Franciszek Sierpiński, in another transcription - Sierpiński (Polish: Wacław Franciszek Sierpiński; March 14, 1882, Warsaw - October 21, 1969, ibid.) - Polish mathematician and teacher, known for his works on set theory, the axiom of choice, the continuum hypothesis, number theory , function theory, and topology. Author of 724 articles and 50 books.

Tetrahedron (Bottrop)

Tetrahedron (German: Tetraeder) is a steel structure in the form of a tetrahedron with an edge length of 60 m, supported by four 9-meter concrete supports, used as an observation deck, in the city of Bottrop (North Rhine-Westphalia). The tetrahedron is located on top of the Beckstraße waste heap (German: Beckstraße) of the Prosper-Haniel mine (de: Bergwerk Prosper-Haniel) at an altitude of 105 m above sea level. From the top observation deck you can see views of the cities of Bottrop, Essen, Oberhausen, Gladbeck. With good visibility, the viewing range reaches 40 km and even allows you to distinguish the Rheinturm television tower in Düsseldorf.

The Bottrop Tetrahedron is the thematic point of the regional project "Path of Industrial Culture" of the Ruhr region.

Pascal's triangle

Pascal's triangle is an infinite table of binomial coefficients having a triangular shape. In this triangle, there are ones at the top and on the sides. Each number is equal to the sum of the two numbers above it. The lines of the triangle are symmetrical about the vertical axis. Named after Blaise Pascal. The numbers that make up Pascal's triangle arise naturally in algebra, combinatorics, probability theory, mathematical analysis, and number theory.

Fractal

Fractal (lat. fractus - crushed, broken, broken) is a set that has the property of self-similarity (an object that exactly or approximately coincides with a part of itself, that is, the whole has the same shape as one or more parts). In mathematics, fractals are understood as sets of points in Euclidean space that have a fractional metric dimension (in the sense of Minkowski or Hausdorff), or a metric dimension different from the topological one, so they should be distinguished from other geometric figures limited by a finite number of links. Self-similar figures that repeat themselves a finite number of times are called prefractals.

The first examples of self-similar sets with unusual properties appeared in the 19th century as a result of the study of continuous non-differentiable functions (for example, the Bolzano function, the Weierstrass function, the Cantor set). The term “fractal” was introduced by Benoit Mandelbrot in 1975 and became widely known with the publication of his book “Fractal Geometry of Nature” in 1977. Fractals gained particular popularity with the development of computer technologies, which made it possible to effectively visualize these structures.

The word "fractal" is used not only as a mathematical term. A fractal can be called an object that has at least one of the following properties:

It has a non-trivial structure at all scales. This is in contrast to regular figures (such as a circle, ellipse, graph of a smooth function): if you consider a small fragment of a regular figure on a very large scale, it will look like a fragment of a straight line. For a fractal, increasing the scale does not lead to a simplification of the structure, that is, on all scales you can see an equally complex picture.

Is self-similar or approximately self-similar.

It has a fractional metric dimension or a metric dimension that exceeds the topological one. Many objects in nature have fractal properties, for example: coasts, clouds, tree crowns, snowflakes, the circulatory system, alveoli.

Fractal dimension

Fractal dimension(English fractal dimension) - one of the ways to determine the dimension of a set in metric space. Fractal dimension n-dimensional set can be defined using the formula:

D = − lim ε → 0 ln ⁡ (N ε) ln ⁡ (ε) (\displaystyle D=-\lim \limits _(\varepsilon \to 0)(\frac (\ln(N_(\varepsilon ))) (\ln(\varepsilon)))), Where N ε (\displaystyle N_(\varepsilon ))- minimum number n-dimensional “balls” of radius ε (\displaystyle \varepsilon), necessary to cover the set.

The fractal dimension can take a non-integer numeric value.

The basic idea of ​​fractured dimension has a long history in the field of mathematics, but it was the term itself that was coined by Benoit Mandelbrot in 1967 in his article on self-similarity, in which he described fractional dimension. In this article, Mandelbrot referred to previous work by Lewis Fry Richardson describing the counterintuitive idea that the measured length of a shoreline depends on the length of a measuring stick (see Figure 1). Following this idea, the fractal dimension of a coastline corresponds to the ratio of the number of poles (at a certain scale) needed to measure the length of the coastline to the chosen scale of the pole. There are several formal mathematical definitions [⇨] of fractal dimension that build on this basic concept of a change in an element with a change in scale.

One elementary example is the fractal dimension of the Koch snowflake. Its topological dimension is 1, but it is by no means a rectifiable curve, since the length of the curve between any two points of a Koch snowflake is infinity. No part of a curve, however small, is a straight line segment. Rather, Koch's snowflake consists of an infinite number of segments connected at different angles. The fractal dimension of a curve can be explained intuitively by suggesting that a fractal line is an object too detailed (detailed) to be one-dimensional, but not complex enough to be two-dimensional. Therefore, its dimension is better described not by the usual topological dimension 1, but by its fractal dimension, equal in this case to a number lying in the interval between 1 and 2.

Fractal art

Fractal art is a form of algorithmic art created by computing fractal objects and presenting the results of the calculations as still images, animations, and automatically generated media files. Fractal art began in the mid-1980s. It is a genre of computer art and digital art that is part of new media art. At the same time, fractal art is one of the areas of the so-called “scientific art”.

Fractal art is rarely created by hand. It is usually created indirectly by software that generates fractals through three steps: setting the parameters of the corresponding fractal software; performing possibly lengthy calculations; and product evaluations. In some cases, other graphics programs are used to further process the generated images. Non-fractal images can also be included in a work of art. The Julia Set and the Mandelbrot Set are considered icons of fractal art.

Characteristics
The simplest fractals

To get it, you need to take an (equilateral) triangle with an interior, draw middle lines in it and throw out the central one of the four small triangles formed. Then you need to repeat the same steps with each of the remaining three triangles, etc. The picture shows the first three steps, and in the flash demonstration you can practice and get steps up to the tenth.

Throwing out the central triangles is not the only way to end up with a Sierpinski triangle. You can move “in the opposite direction”: take an initially “empty” triangle, then complete the triangle formed by the middle lines in it, then do the same in each of the three corner triangles, etc. At first, the figures will be very different, but with As the iteration number increases, they will become more and more similar to each other, and in the limit they will coincide.

The next way to obtain a Sierpinski triangle is even more similar to the usual scheme for constructing geometric fractals by replacing parts of the next iteration with a scaled fragment. Here, at each step, the segments that make up the broken line are replaced with a broken line of three links (it itself is obtained in the first iteration). You need to lay this broken line alternately to the right and then to the left. It can be seen that already the eighth iteration is very close to the fractal, and the further it goes, the closer the line will get to it.

But that’s not all. It turns out that the Sierpinski triangle is obtained as a result of one of the varieties of random walk of a point on a plane. This method is called the "Chaos game". With its help you can build some other fractals.

The essence of the “game” is this. A regular triangle is fixed on a plane A 1 A 2 A 3. Mark any starting point B 0 . Then randomly select one of the three vertices of the triangle and mark the point B 1 - the middle of a segment with ends at this vertex and at B 0 (in the figure on the right, the vertex was randomly selected A 1). The same is repeated with a point B 1 to get B 2. Then they get the points B 3 , B 4, etc. It is important that the point “jump” randomly, that is, that each time the vertex of the triangle is chosen randomly, regardless of what was chosen in the previous steps. It's amazing that if you mark points from a sequence B i, then the Sierpinski triangle will soon begin to appear. Below is what happens when 100, 500 and 2500 points are marked.

Some properties

Options

Carpet (square, napkin) by Sierpinski. The square version was described by Wacław Sierpinski in 1916. He managed to prove that any curve that can be drawn on a plane without self-intersections is homeomorphic to some subset of this holey square. Like a triangle, a square can be made from different designs. On the right is the classic method: dividing the square into 9 parts and throwing away the central part. Then the same is repeated for the remaining 8 squares, etc.

Like a triangle, a square has zero area. The fractal dimension of a Sierpinski carpet is equal to log 3 8, calculated similarly to the dimension of a triangle.

Sierpinski Pyramid. One of the three-dimensional analogues of the Sierpinski triangle. It is constructed in a similar way, taking into account the three-dimensionality of what is happening: 5 copies of the initial pyramid, compressed twice, make up the first iteration, its 5 copies will make up the second iteration, etc. The fractal dimension is equal to log 2 5. The figure has zero volume (at each step half the volume is thrown out), but at the same time the surface area is preserved from iteration to iteration, and for the fractal it is the same as for the initial pyramid.

Menger's sponge. Generalization of the Sierpinski carpet into three-dimensional space. To build a sponge, you need an endless repetition of the procedure: each of the cubes that make up the iteration is divided into 27 three times smaller cubes, from which the central one and its 6 neighbors are thrown out. That is, each cube generates 20 new ones, three times smaller. Therefore, the fractal dimension is log 3 20. This fractal is a universal curve: any curve in three-dimensional space is homeomorphic to some subset of the sponge. The sponge has zero volume (since at each step it is multiplied by 20/27), but it has an infinitely large area.

L
Oman line:

N – number of segments, size A.

D – “degree of bending”

N=(1/a)D; S=N*a ; S=(1/a)D-1

TO
Riva Koch

2) N=4L=1/3S(4)=4/3

N=16 L=1/9S(16)=16/9

Fractal dimension:

D=lg4 /lg3=1.26…

Fractal dimension of a set

The volume of the fractal in its embedding space is always zero. It, however, can be non-zero in a space of lower dimension. To determine the dimension of this space D, let's break everything n-dimensional space into small cubes with edge length ε and volume ε n- Fig. 1. Let N(ε ) is the minimum number of cubes that together completely cover the fractal set, then by definition

The existence of this limit means the fractal volume is finite in D-dimensional space: with small ε

and unlike the usual dimension D can be a fractional value, which is what it most often is for fractal sets.

Obviously, for ordinary sets this definition leads to well-known results. So for the multitude N isolated points we have N(ε ) =N and therefore

For a segment, a smooth line of length is sufficient L:N(ε ) =L/ε and therefore D= 1. For the site S two-dimensional surface: N(ε ) =S/ε 2 and D= 2, etc..

Recursive algorithm for constructing constructive fractals.

1. Sierpinski triangle

Sierpinski triangle

Sierpinski triangle- a fractal, one of the two-dimensional analogues of the Cantor set proposed by the Polish mathematician Sierpinski in 1915. Also known as the Sierpinski "grid" or "napkin".

Construction

A solid equilateral triangle is taken, and in the first step the interior of the middle triangle is removed from the center. At the second step, the three middle triangles are removed from the three remaining triangles, etc. After endless repetition of this procedure, a subset of the solid triangle remains - the Sierpinski triangle.

Construction of the Sierpinski triangle

The Sierpinski triangle can also be obtained using the following algorithm:

Take three points on the plane and draw a triangle.

Randomly select any point inside the triangle, and move half the distance from this point to any of the three vertices of the triangle.

Mark the current position.

Repeat from step 2.

The concepts of fractal and fractal geometry, which appeared in the late 70s, have become firmly established among mathematicians and programmers since the mid-80s. The word fractal is derived from the Latin fractus and means consisting of fragments. It was proposed by Benoit Mandelbrot in 1975 to refer to the irregular but self-similar structures with which he was concerned. The birth of fractal geometry is usually associated with the publication of Mandelbrot’s book “The Fractal Geometry of Nature” in 1977. His works used the scientific results of other scientists who worked in the period 1875-1925 in the same field (Poincaré, Fatou, Julia, Cantor, Hausdorff But only in our time has it been possible to combine their work into a single system.
The role of fractals in computer graphics today is quite large. They come to the rescue, for example, when it is necessary, using several coefficients, to define lines and surfaces of very complex shapes. From the point of view of computer graphics, fractal geometry is indispensable when generating artificial clouds, mountains, and sea surfaces. In fact, a way has been found to easily represent complex non-Euclidean objects, the images of which are very similar to natural ones.
One of the main properties of fractals is self-similarity. In the simplest case, a small part of a fractal contains information about the entire fractal. Mandelbrot's definition of a fractal is: "A fractal is a structure consisting of parts that are in some sense similar to the whole."

There are a large number of mathematical objects called fractals (Sierpinski triangle, Koch snowflake, Peano curve, Mandelbrot set and Lorentz attractors). Fractals describe with great accuracy many physical phenomena and formations of the real world: mountains, clouds, turbulent (vortex) flows, roots, branches and leaves of trees, blood vessels, which is far from corresponding to simple geometric figures. For the first time, Benoit Mandelbrot spoke about the fractal nature of our world in his seminal work “Fractal Geometry of Nature”.
The term fractal was introduced by Benoit Mandelbrot in 1977 in his fundamental work Fractals, Form, Chaos and Dimension. According to Mandelbrot, the word fractal comes from the Latin words fractus - fractional and frangere - to break, which reflects the essence of a fractal as a “broken”, irregular set.

Classification of fractals.

For that In order to present the whole variety of fractals, it is convenient to resort to their generally accepted classification. There are three classes of fractals.

1. Geometric fractals.

Fractals of this class are the most visual. In the two-dimensional case, they are obtained using a broken line (or surface in the three-dimensional case), called a generator. In one step of the algorithm, each of the segments that make up the broken line is replaced by polyline-generator on an appropriate scale. As a result of endless repetition of this procedure, a geometric fractal is obtained.

Let's look at an example of one of these fractal objects - the triadic Koch curve.

Construction of the triadic Koch curve.

Let's take a straight segment of length 1. Let's call it seed. Let's divide the seed into three equal parts 1/3 long, discard the middle part and replace it with a broken line of two links 1/3 long.

We will get a broken line consisting of 4 links with a total length of 4/3, so we call first generation.

In order to move to the next generation of the Koch curve, it is necessary to discard and replace the middle part of each link. Accordingly, the length of the second generation will be 16/9, the third – 64/27. if we continue this process ad infinitum, the result is a triadic Koch curve.

Let us now consider the properties of the triadic Koch curve and find out why fractals were called “monsters”.

Firstly, this curve has no length - as we have seen, with the number of generations its length tends to infinity.

Secondly, it is impossible to construct a tangent to this curve - each of its points is an inflection point at which the derivative does not exist - this curve is not smooth.

Length and smoothness are the fundamental properties of curves, which are studied both by Euclidean geometry and by the geometry of Lobachevsky and Riemann. Traditional methods of geometric analysis turned out to be inapplicable to the triadic Koch curve, so the Koch curve turned out to be a monster - a “monster” among the smooth inhabitants of traditional geometries.

Construction of the Harter-Haithway "dragon".

To obtain another fractal object, you need to change the construction rules. Let the forming element be two equal segments connected at right angles. In the zero generation replace the unit segment with this forming element so that the corner is on top. We can say that with such a replacement there is a displacement of the middle of the link. When constructing subsequent generations, the rule is followed: the very first link on the left is replaced with a forming element so that the middle of the link is shifted to the left of the direction of movement, and when replacing subsequent links, the directions of displacement of the middles of the segments must alternate. The figure shows the first few generations and the 11th generation of the curve built according to the principle described above. A curve with n tending to infinity is called the Harter-Haithway dragon.
In computer graphics, the use of geometric fractals is necessary when obtaining images of trees and bushes. Two-dimensional geometric fractals are used to create three-dimensional textures (patterns on the surface of an object).

2.Algebraic fractals

This is the largest group of fractals. They are obtained using nonlinear processes in n-dimensional spaces. Two-dimensional processes are the most studied. When interpreting a nonlinear iterative process as a discrete dynamic system, one can use the terminology of the theory of these systems: phase portrait, steady-state process, attractor, etc.
It is known that nonlinear dynamic systems have several stable states. The state in which the dynamic system finds itself after a certain number of iterations depends on its initial state. Therefore, each stable state (or, as they say, attractor) has a certain region of initial states, from which the system will necessarily fall into the final states under consideration. Thus, the phase space of the system is divided into areas of attraction of attractors. If the phase space is a two-dimensional space, then by coloring the areas of attraction with different colors, one can obtain a color phase portrait of this system (iterative process). By changing the color selection algorithm, you can get complex fractal patterns with bizarre multicolor patterns. A surprise for mathematicians was the ability to generate very complex non-trivial structures using primitive algorithms.

Mandelbrot set.

As an example, consider the Mandelbrot set. The algorithm for its construction is quite simple and is based on a simple iterative expression: Z = Z * Z + C, Where Zi And C- complex variables. Iterations are performed for each starting point from a rectangular or square region - a subset of the complex plane. The iterative process continues until Z will not go beyond the circle of radius 2, the center of which lies at the point (0,0), (this means that the attractor of the dynamical system is at infinity), or after a sufficiently large number of iterations (for example, 200-500) Z will converge to some point on the circle. Depending on the number of iterations during which Z remained inside the circle, you can set the color of the point C(If Z remains inside the circle for a sufficiently large number of iterations, the iteration process stops and this raster point is painted black).

3. Stochastic fractals

Another well-known class of fractals are stochastic fractals, which are obtained if some of its parameters are randomly changed in an iterative process. In this case, the resulting objects are very similar to natural ones - asymmetrical trees, rugged coastlines, etc. Two-dimensional stochastic fractals are used in terrain and sea surface modeling.
There are other classifications of fractals, for example, dividing fractals into deterministic (algebraic and geometric) and non-deterministic (stochastic).

About the use of fractals

First of all, fractals are a field of amazing mathematical art, when with the help of the simplest formulas and algorithms, pictures of extraordinary beauty and complexity are obtained! Leaves, trees and flowers are often visible in the contours of the constructed images.

Some of the most powerful applications of fractals lie in computer graphics. Firstly, this is fractal compression of images, and secondly, the construction of landscapes, trees, plants and the generation of fractal textures. Modern physics and mechanics are just beginning to study the behavior of fractal objects. And, of course, fractals are used directly in mathematics itself.
The advantages of fractal image compression algorithms are the very small size of the packed file and short image recovery time. Fractal packed images can be scaled without causing pixelation. But the compression process takes a long time and sometimes lasts for hours. The fractal lossy packaging algorithm allows you to set the compression ratio, similar to the jpeg format. The algorithm is based on searching for large pieces of the image that are similar to some small pieces. And only which piece is similar to which is written to the output file. When compressing, a square grid is usually used (pieces are squares), which leads to a slight angularity when restoring the image; a hexagonal grid does not have this drawback.
Iterated has developed a new image format, "Sting", which combines fractal and "wave" (such as jpeg) lossless compression. The new format allows you to create images with the possibility of subsequent high-quality scaling, and the volume of graphic files is 15-20% of the volume of uncompressed images.
The tendency of fractals to resemble mountains, flowers and trees is exploited by some graphic editors, for example, fractal clouds from 3D studio MAX, fractal mountains in World Builder. Fractal trees, mountains and entire landscapes are defined by simple formulas, are easy to program and do not break up into separate triangles and cubes when approached.
One cannot ignore the use of fractals in mathematics itself. In set theory, the Cantor set proves the existence of perfect nowhere dense sets; in measure theory, the self-affine function "Cantor's Ladder" is a good example of a distribution function of a singular measure.
In mechanics and physics, fractals are used due to their unique property of repeating the outlines of many natural objects. Fractals allow you to approximate trees, mountain surfaces and cracks with higher accuracy than approximations using sets of segments or polygons (with the same amount of stored data). Fractal models, like natural objects, have a “roughness”, and this property is preserved no matter how large the magnification of the model is. The presence of a uniform measure on fractals allows one to apply integration, potential theory, and use them instead of standard objects in already studied equations.
With a fractal approach, chaos ceases to be blue disorder and acquires a fine structure. Fractal science is still very young and has a great future ahead of it. The beauty of fractals is far from being exhausted and will still give us many masterpieces - those that delight the eye, and those that bring true pleasure to the mind.

About constructing fractals

Successive approximation method

Looking at this picture, it is not difficult to understand how you can build a self-similar fractal (in this case, the Sierpinski pyramid). We need to take a regular pyramid (tetrahedron), then cut out its middle (octahedron), resulting in four small pyramids. With each of them we perform the same operation, etc. This is a somewhat naive but clear explanation.

Let us consider the essence of the method more strictly. Let there be some IFS system, i.e. compression mapping system S=(S 1 ,...,S m ) S i:R n ->R n (for example, for our pyramid the mappings look like S i (x )=1/2*x+o i , where o i are the vertices of the tetrahedron, i=1,..,4). Then we choose some compact set A 1 in R n (in our case we choose a tetrahedron). And we determine by induction the sequence of sets A k:A k+1 =S 1 (A k ) U...U S m (A k ). It is known that sets A k with increasing k approximate the desired attractor of the system better and better S.

Note that each of these iterations is an attractor recurrent system of iterated functions(English term Digraph IFS, RIFS and also Graph-directed IFS) and therefore they are easy to build using our program.

Point-by-point or probabilistic method

This is the easiest method to implement on a computer. For simplicity, we consider the case of a flat self-affine set. So, let (S 1,..,S m) be some system of affine contractions. Mappings S i are representable in the form: S i (x)=A i (x-o i)+o i, where A i is a fixed matrix of size 2x2 and o i is a two-dimensional column vector.

· Let's take the fixed point of the first mapping S 1 as the starting point:
x : = o1;
Here we take advantage of the fact that all fixed points of compression S 1 ,..,S m belong to the fractal. You can select an arbitrary point as the starting point and the sequence of points generated by it will be drawn to a fractal, but then several extra points will appear on the screen.

· Let's mark the current point x= (x 1 ,x 2) on the screen:
putpixel(x 1 ,x 2 ,15);

· Let's randomly choose a number j from 1 to m and recalculate the coordinates of point x:
j:=Random (m )+1;
x:=S j (x);

· We go to step 2, or, if we have done a sufficiently large number of iterations, we stop.
Note. If the compression ratios of the mappings S i are different, then the fractal will be filled with points unevenly. If the mappings S i are similar, this can be avoided by slightly complicating the algorithm. To do this, at the 3rd step of the algorithm, the number j from 1 to m must be chosen with probabilities p 1 =r 1 s,..,p m =r m s, where r i denote the compression coefficients of the mappings Si, and the number s (called the similarity dimension) is found from the equation r 1 s +...+r m s =1. The solution to this equation can be found, for example, by Newton's method.

About fractals and their algorithms

Fractal comes from the Latin adjective "fractus", and in translation means consisting of fragments, and the corresponding Latin verb "frangere" means to break, that is, to create irregular fragments. The concepts of fractal and fractal geometry, which appeared in the late 70s, have become firmly established among mathematicians and programmers since the mid-80s. The term was coined by Benoit Mandelbrot in 1975 to refer to the irregular but self-similar structures with which he was concerned. The birth of fractal geometry is usually associated with the publication of Mandelbrot’s book “The Fractal Geometry of Nature” in 1977. His works used the scientific results of other scientists who worked in the period 1875-1925 in the same field (Poincaré, Fatou, Julia, Cantor, Hausdorff).

Adjustments

Let me make some adjustments to the algorithms proposed in the book by H.-O. Peitgen and P.H. Richter “The Beauty of Fractals” M. 1993 purely to eradicate typos and facilitate understanding of the processes since after studying them much remained a mystery to me. Unfortunately, these “understandable” and “simple” algorithms lead a rocking lifestyle.

The construction of fractals is based on a certain nonlinear function of a complex process with feedback z = > z 2 +c since z and c -k are complex numbers, then z = x + iy , c = p + iq it is necessary to decompose it into x and y in order to go to a plane more realistic for the common man:

x(k+1)=x(k) 2 -y(k) 2 + p,
y(k+1)=2*x(k)*y(k) + q.

A plane consisting of all pairs (x,y ) can be considered as for fixed values R and q, and with dynamic ones. In the first case, by going through all the points (x ,y) planes and coloring them depending on the number of function repetitions necessary to exit the iterative process or not coloring them (black color) when the permissible maximum repetitions are exceeded, we obtain a mapping of the Julia set. If, on the contrary, we determine the initial pair of values ​​(x,y) and trace its coloristic fate with dynamically changing values ​​of the parameters p and q, then we obtain images called Mandelbrot sets.

On the question of algorithms for coloring fractals.

Usually the body of a set is represented as a black field, although it is obvious that black color can be replaced by any other, but this is also a little interesting result. Getting an image of a set colored in all colors is a task that cannot be solved using cyclic operations because the number of iterations of the sets forming the body is equal to the maximum possible and is always the same. It is possible to color a set in different colors by using the result of checking the loop exit condition (z_magnitude) or something similar to it, but with other mathematical operations, as a color number.

Application of a "fractal microscope"

to demonstrate boundary phenomena.

Attractors are centers leading the struggle for dominance on the plane. A boundary appears between the attractors, representing a florid pattern. By increasing the scale of consideration within the boundaries of the set, one can obtain non-trivial patterns that reflect the state of deterministic chaos - a common phenomenon in the natural world.

The objects studied by geographers form a system with very complexly organized boundaries, and therefore their identification becomes not a simple practical task. Natural complexes have cores of typicality that act as attractors that lose their influence on the territory as it moves away.

Using a fractal microscope for the Mandelbrot and Julia sets, one can form an idea of ​​boundary processes and phenomena that are equally complex regardless of the scale of consideration and thus prepare the specialist’s perception for an encounter with a dynamic and seemingly chaotic natural object in space and time, for an understanding of fractal geometry nature. The multicolored colors and fractal music will definitely leave a deep imprint in the minds of students.

Thousands of publications and vast Internet resources are devoted to fractals, but for many specialists far from computer science, this term seems completely new. Fractals, as objects of interest to specialists in various fields of knowledge, should receive a proper place in computer science courses.

Examples

SIEPINSKI GRID

This is one of the fractals that Mandelbrot experimented with when developing the concepts of fractal dimensions and iterations. Triangles formed by connecting the midpoints of a larger triangle are cut out from the main triangle, forming a triangle with more holes. In this case, the initiator is the large triangle and the template is the operation of cutting out triangles similar to the larger one. You can also get a three-dimensional version of a triangle by using an ordinary tetrahedron and cutting out small tetrahedrons. The dimension of such a fractal is ln3/ln2 = 1.584962501. To obtain Sierpinski carpet, take a square, divide it into nine squares, and cut out the middle one. We will do the same with the rest, smaller squares. Eventually, a flat fractal grid is formed, having no area but with infinite connections. In its spatial form, the Sierpinski sponge is transformed into a system of end-to-end forms, in which each end-to-end element is constantly replaced by its own kind. This structure is very similar to a section of bone tissue. Someday such repeating structures will become an element of building structures. Their statics and dynamics, Mandelbrot believes, deserve close study.

SIERPINSKI FRACTAL

Do not confuse this fractal with the Sierpinski lattice. These are two completely different objects. In this fractal, the initiator and generator are the same. At each iteration, a smaller copy of the initiator is added to each corner of the generator, and so on. If an infinite number of iterations were performed when creating this fractal, it would occupy the entire plane, without leaving a single hole. Therefore, its fractal dimension is ln9/ln3 = 2.0.

KOCH CURVE

The Koch curve is one of the most typical deterministic fractals. It was invented in the nineteenth century by a German mathematician named Helge von Koch, who, while studying the work of Georg Kontor and Karl Weierstrasse, came across descriptions of some strange curves with unusual behavior. The initiator is a straight line. The generator is an equilateral triangle, the sides of which are equal to a third of the length of the larger segment. These triangles are added to the middle of each segment over and over again. In his research, Mandelbrot experimented extensively with Koch curves, and produced figures such as Koch Islands, Koch Crosses, Koch Snowflakes, and even three-dimensional representations of the Koch curve by using a tetrahedron and adding smaller tetrahedrons to each of its faces. The Koch curve has dimension ln4/ln3 = 1.261859507.

MANDELBROT FRACTAL

This is NOT the Mandelbrot set, which you see quite often. The Mandelbrot set is based on nonlinear equations and is a complex fractal. This is also a variant of the Koch curve, although this object is not similar to it. The initiator and generator are also different from those used to create fractals based on the Koch curve principle, but the idea remains the same. Instead of joining equilateral triangles to a curve segment, squares are joined to a square. Due to the fact that this fractal occupies exactly half of the allotted space at each iteration, it has a simple fractal dimension of 3/2 = 1.5.

FRACTALS STAR AND SNOWFLAKE

Both of these objects are not classical fractals and they were not invented by Mandelbrot or any other famous mathematician. I just created these fractals out of interest and to experiment with programming. Both the initiator and generator here are a figure formed by connecting the midpoints of the sides with the midpoints of the opposite sides in a regular hexagon. Moreover, I can only suspect the dimension of these fractals.

DARER PENTAGON

A fractal looks like a bunch of pentagons squeezed together. In fact, it is formed by using a pentagon as an initiator and isosceles triangles in which the ratio of the larger side to the smaller side is exactly equal to the so-called golden ratio (1.618033989 or 1/(2cos72)) as a generator. These triangles are cut from the middle of each pentagon, resulting in a shape that looks like 5 small pentagons glued to one large one. A variant of this fractal can be obtained by using a hexagon as an initiator. This fractal is called the Star of David and it is quite similar to a hexagonal version of the Koch Snowflake. The fractal dimension of the Darer pentagon is ln6/ln (1+g), where g is the ratio of the length of the larger side of the triangle to the length of the smaller one. In this case, g is the Golden Ratio, so the fractal dimension is approximately 1.86171596. Fractal dimension of the Star of David ln6/ln3 or 1.630929754.

HILBERT CURVE

This fractal is very similar to the Labyrinth Fractal, except for the fact that the width of the letter U, which is the generator, does not change with each iteration. However, unlike the Labyrinth Fractal, the Hilbert curve, also called the Hilbert Hotel, has one single fractal dimension, which is exactly 2.0, since with an infinite number of iterations, it will occupy the entire plane. fractal and then do the same with a small area of ​​that area, the two magnifications will be significantly different from each other. The two images will be very similar in detail, but they will not be completely identical. Figure 1. Mandelbrot set approximation Compare, for example, the pictures of the Mandelbrot set shown here, one of which was obtained by enlarging a certain area of ​​the other. As you can see, they are absolutely not identical, although on both we see a black circle, from which flaming tentacles extend in different directions. These elements are repeated indefinitely in the Mandelbrot set in decreasing proportions. Deterministic fractals are linear, whereas complex fractals are not. Being nonlinear, these fractals are generated by what Mandelbrot called nonlinear algebraic equations. A good example is the process Zn+1=ZnI + C, which is the equation used to construct the Mandelbrot and Julia set of the second degree. Solving these mathematical equations involves complex and imaginary numbers. When the equation is interpreted graphically in the complex plane, the result is a strange figure in which straight lines turn into curves and self-similarity effects appear, albeit not without deformations, at various scale levels. At the same time, the whole picture as a whole is unpredictable and very chaotic. As you can see by looking at the pictures, complex fractals are indeed very complex and cannot be created without the help of a computer. To obtain colorful results, this computer must have a powerful mathematical coprocessor and a high-resolution monitor. Unlike deterministic fractals, complex fractals are not calculated in 5-10 iterations. Almost every point on a computer screen is like a separate fractal. During mathematical processing, each point is treated as a separate drawing. Each point corresponds to a specific value. The equation is built in for each point and is performed, for example, 1000 iterations. To obtain a relatively undistorted image in a time period acceptable for home computers, it is possible to carry out 250 iterations for one point. Most of the fractals we see today are beautifully colored. Perhaps fractal images gain such great aesthetic significance precisely because of their color schemes. After the equation is calculated, the computer analyzes the results. If the results remain stable, or fluctuate around a certain value, the dot usually turns black. If the value at one step or another tends to infinity, the point is painted in a different color, maybe blue or red. During this process, the computer assigns colors to all motion speeds. Typically, fast moving dots are colored red, while slower ones are colored yellow, and so on. Dark spots are probably the most stable. Complex fractals are different from deterministic in the sense that they are infinitely complex, but at the same time can be generated by a very simple formula. Deterministic fractals do not require formulas or equations. Just take some drawing paper and you can build a Sierpinski sieve up to 3 or 4 iterations without any difficulty. Try this with lots of Julia! It's easier to go measure the length of England's coastline! MANDELBROT SET Fig 2. Mandelbrot set Mandelbrot and Julia sets are probably the two most common among complex fractals. They can be found in many scientific journals, book covers, postcards, and computer screen savers. The Mandelbrot set, which was constructed by Benoit Mandelbrot, is probably the first association that people have when they hear the word fractal. This fractal, which resembles a carding machine with flaming tree-like and circular areas attached to it, is generated by the simple formula Zn+1=Zna+C, where Z and C are complex numbers and a is a positive number. The Mandelbrot set, which can most often be seen, is the Mandelbrot set of the 2nd degree, that is, a = 2. The fact that the Mandelbrot set is not only Zn+1=ZnІ+C, but a fractal, the indicator in the formula of which can be any positive number, has misled many. On this page you see an example of the Mandelbrot set for various values ​​of the exponent a. Figure 3. The appearance of bubbles at a=3.5 The process Z=Z*tg (Z+C) is also popular. By including the tangent function, the result is a Mandelbrot set surrounded by an area resembling an apple. When using the cosine function, air bubble effects are obtained. In short, there are an infinite number of ways to configure the Mandelbrot set to produce different beautiful pictures. A LOT OF JULIA Surprisingly, Julia sets are formed according to the same formula as the Mandelbrot set. The Julia set was invented by the French mathematician Gaston Julia, after whom the set was named. The first question that arises after a visual acquaintance with the Mandelbrot and Julia sets is “if both fractals are generated according to the same formula, why are they so different?” First look at the pictures of the Julia set. Oddly enough, there are different types of Julia sets. When drawing a fractal using different starting points (to begin the iteration process), different images are generated. This only applies to the Julia set. Figure 4. Julia set Although it can't be seen in the picture, a Mandelbrot fractal is actually many Julia fractals connected together. Each point (or coordinate) of the Mandelbrot set corresponds to a Julia fractal. Julia sets can be generated using these points as initial values ​​in the equation Z=ZI+C. But this does not mean that if you select a point on the Mandelbrot fractal and enlarge it, you can get the Julia fractal. These two points are identical, but only in a mathematical sense. If you take this point and calculate it using this formula, you can get the Julia fractal, corresponding to a certain point of the Mandelbrot fractal.