2.Электрическое поле. Электрическое поле точечного заряда. Силовые линии.

По современным представлениям, электрические заряды не действуют друг на друга непосредственно. Каждое заряженное тело создает в окружающем пространстве электрическое поле . Это поле оказывает силовое действие на другие заряженные тела. Главное свойство электрического поля – действие на электрические заряды с некоторой силой. Таким образом, взаимодействие заряженных тел осуществляется не непосредственным их воздействием друг на друга, а через электрические поля, окружающие заряженные тела.

Электрическое поле, окружающее заряженное тело, можно исследовать с помощью так называемого пробного заряда – небольшого по величине точечного заряда, который не производит заметного перераспределения исследуемых зарядов.

Для количественного определения электрического поля вводится силовая характеристика напряженность электрического поля .

Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на положительный пробный заряд, помещенный в данную точку пространства, к величине этого заряда:

Напряженность электрического поля – векторная физическая величина. Направление вектора в каждой точке пространства совпадает с направлением силы, действующей на положительный пробный заряд.

Электрическое поле неподвижных и не меняющихся со временем зарядов называется электростатическим . Во многих случаях для краткости это поле обозначают общим термином – электрическое поле

Если с помощью пробного заряда исследуется электрическое поле, создаваемое несколькими заряженными телами, то результирующая сила оказывается равной геометрической сумме сил, действующих на пробный заряд со стороны каждого заряженного тела в отдельности. Следовательно, напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряженностей электрических полей, создаваемых в той же точке зарядами в отдельности:

Это поле называется кулоновским . В кулоновском поле направление вектора зависит от знака заряда Q : если Q > 0, то вектор направлен по радиусу от заряда, если Q < 0, то вектор направлен к заряду.

Для наглядного изображения электрического поля используют силовые линии . Эти линии проводят так, чтобы направление вектора в каждой точке совпадало с направлением касательной к силовой линии (рис. 1.2.1). При изображении электрического поля с помощью силовых линий, их густота должна быть пропорциональна модулю вектора напряженности поля.

Силовые линии кулоновских полей положительных и отрицательных точечных зарядов изображены на рис. 1.2.2. Так как электростатическое поле, создаваемое любой системой зарядов, может быть представлено в виде суперпозиции кулоновских полей точечных зарядов, изображенные на рис. 1.2.2 поля можно рассматривать как элементарные структурные единицы («кирпичики») любого электростатического поля.

Кулоновское поле точечного заряда Q удобно записать в векторной форме. Для этого нужно провести радиус-вектор от заряда Q к точке наблюдения. Тогда при Q > 0 вектор параллелен а при Q < 0 вектор антипараллелен Следовательно, можно записать:

где r – модуль радиус-вектора .

В качестве примера применения принципа суперпозиции полей на рис. 1.2.3. изображена картина силовых линий поля электрического диполя – системы из двух одинаковых по модулю зарядов разного знака q и –q , расположенных на некотором расстоянии l .

Важной характеристикой электрического диполя является так называемый дипольный момент

где – вектор, направленный от отрицательного заряда к положительному, модуль Диполь может служить электрической моделью многих молекул.

Электрическим дипольным моментом обладает, например, нейтральная молекула воды (H 2 O), так как центры двух атомов водорода располагаются не на одной прямой с центром атома кислорода, а под углом 105° (рис. 1.2.4). Дипольный момент молекулы воды p = 6,2·10 –30 Кл · м.

3.Электростатическая теорема Гаусса. Доказательство теоремы Гаусса для частного случая (точечный заряд расположен внутри сферы радиуса R ). Обобщение теоремы Гаусса на N точечных зарядов. Обобщение теоремы Гаусса на случай непрерывно распределенного заряда. Теорема Гаусса в дифференциальной форме.

Найдем поток вектора Е сквозь сферическую поверхность S, в центре которой находится точечный заряд q.

В этом случае т.к. направления Е и n во всех точках сферической поверхности совпадают.

С учетом напряженности поля точечного заряда и того, что площадь поверхности сферы получим

Алгебраическая величина, зависящая от знака заряда. Например, при q <0 линии Е направлены к заряду и противоположны направлению внешней нормали n . Поэтому в таком случае поток отрицателен <0 .

Пусть замкнутая поверхность вокруг заряда q имеет произвольную форму. Очевидно, что поверхность пересекается тем же числом линий Е, что и поверхность S. Следовательно, поток вектора Е сквозь произвольную поверхность также определяется полученной формулой .

Если заряд будет находиться вне замкнутой поверхности, то, очевидно, сколько линий войдет в замкнутую область, столько же из нее и выйдет. В результате поток вектора Е будет равен нулю.

Если электрическое поле создается системой точечных зарядов то согласно принципу суперпозиции,

Доказательство частного случая:

Теорема Гаусса утверждает:

Поток вектора напряженности электростатического поля через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε 0 .

где R – радиус сферы. Поток Φ через сферическую поверхность будет равен произведению E на площадь сферы 4πR 2 . Следовательно,

Окружим теперь точечный заряд произвольной замкнутой поверхностью S и рассмотрим вспомогательную сферу радиуса R 0 (рис. 1.3.3).

Рассмотрим конус с малым телесным углом ΔΩ при вершине. Этот конус выделит на сфере малую площадку ΔS 0 , а на поверхности S – площадку ΔS . Элементарные потоки ΔΦ 0 и ΔΦ через эти площадки одинаковы. Действительно,

Здесь ΔS" = ΔS cos α – площадка, выделяемая конусом с телесным углом ΔΩ на поверхности сферы радиуса n .

Так как а следовательно Отсюда следует, что полный поток электрического поля точечного заряда через произвольную поверхность, охватывающую заряд, равен потоку Φ 0 через поверхность вспомогательной сферы:

Аналогичным образом можно показать, что, если замкнутая поверхность S не охватывает точечного заряда q , то поток Φ = 0. Такой случай изображен на рис. 1.3.2. Все силовые линии электрического поля точечного заряда пронизывают замкнутую поверхность S насквозь. Внутри поверхности S зарядов нет, поэтому в этой области силовые линии не обрываются и не зарождаются.

Обобщение теоремы Гаусса на случай произвольного распределения зарядов вытекает из принципа суперпозиции. Поле любого распределения зарядов можно представить как векторную сумму электрических полей точечных зарядов. Поток Φ системы зарядов через произвольную замкнутую поверхностьS будет складываться из потоков Φ i электрических полей отдельных зарядов. Если заряд q i оказался внутри поверхности S , то он дает вклад в поток, равный если же этот заряд оказался снаружи поверхности, то вклад его электрического поля в поток будет равен нулю.

Таким образом, теорема Гаусса доказана.

Для любого количества зарядов

Завершающий шаг прост. Он заключается в применении принципа суперпозиции.

Если для каждого точечного заряда поле , создаваемое им (когда остальные заряды отсутствуют), создает через поверхность поток, удовлетворяющий теореме Гаусса (то есть для каждого заряда внутри поверхности, и 0 для каждого снаружи поверхности), то поток от суммарного поля

равен сумме потоков, создаваемых каждым зарядом при отсутствии остальных, равен просто

где суммирование производится только по зарядам внутри поверхности (каждый из тех, что снаружи, дает вклад 0).

Теорема доказана.

ЭЛЕКТРИЧЕСКОЕ СМЕЩЕНИЕ

Основные формулы

 Напряженность электрического поля

E =F /Q ,

где F - сила, действующая на точечный положительный зарядQ , помещенный в данную точку поля.

 Сила, действующая на точечный заряд Q , помещенный в электрическое поле,

F =Q E .

Е электрического поля:

а) через произвольную поверхность S , помещенную в неоднородное поле,

или

,

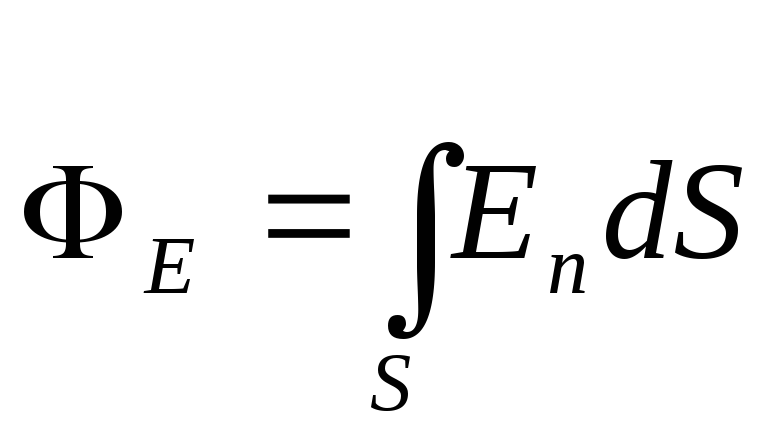где - угол между вектором напряженностиЕ и нормальюn к элементу поверхности; dS - площадь элемента поверхности;E n - проекция вектора напряженности на нормаль;

б) через плоскую поверхность, помещенную в однородное электрическое поле,

Ф E =Е S cos.

 Поток вектора напряженности Е через замкнутую поверхность

,

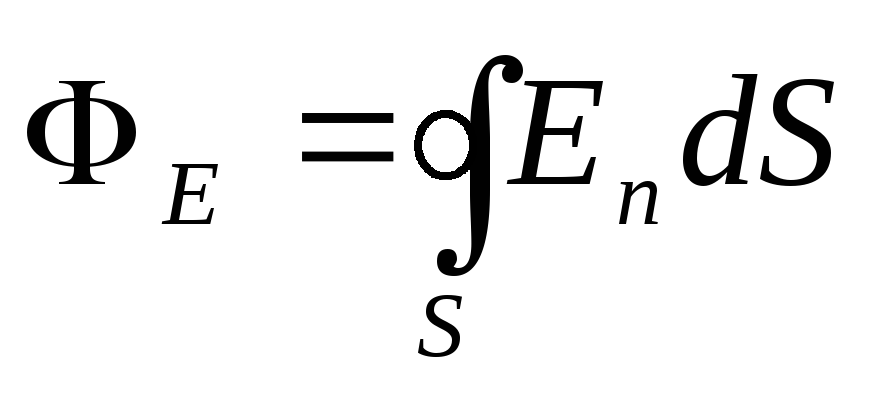где интегрирование ведется по всей поверхности.

 Теорема Остроградского - Гаусса. Поток вектора напряженности Е через любую замкнутую поверхность, охватывающую заряды Q l , Q 2 , . . ., Q n ,

,

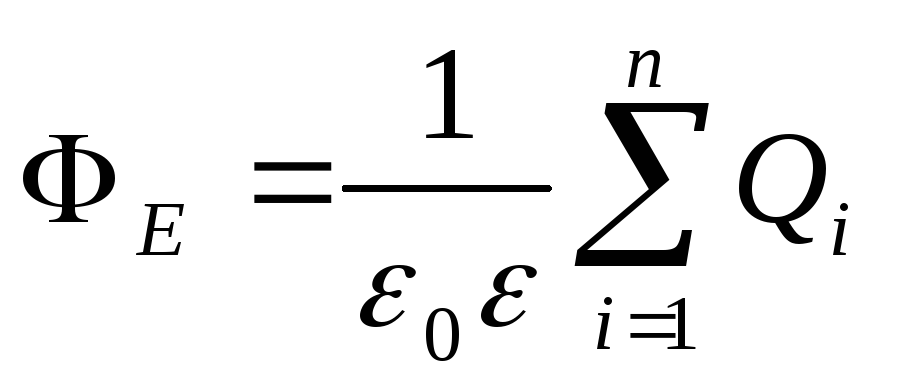где 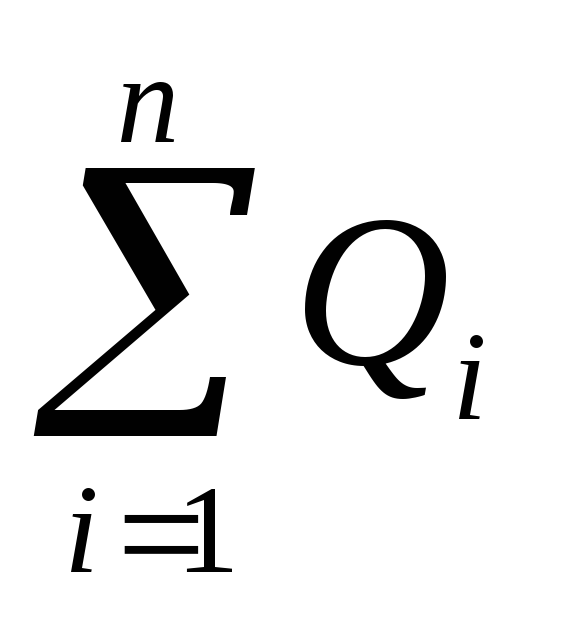- алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности;п - число зарядов.

 Напряженность электрического поля, создаваемого точечным зарядом Q на расстоянииr от заряда,

.

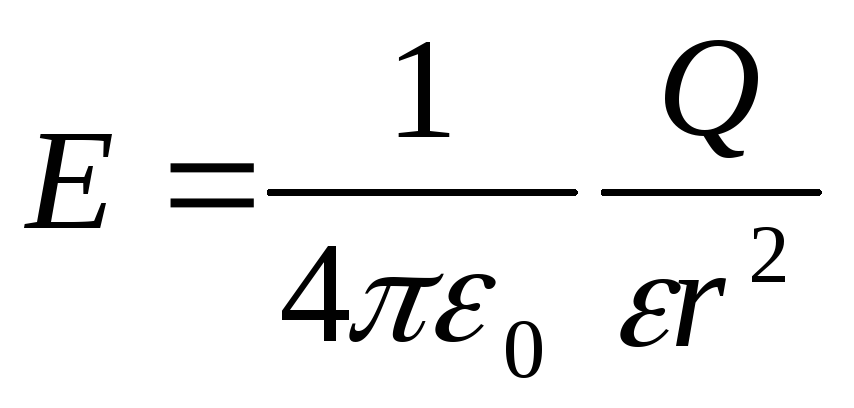Напряженность электрического поля, создаваемого металлической сферой радиусом R, несущей заряд Q ,на расстоянииr от центра сферы:

а) внутри сферы (r<.R)

б) на поверхности сферы (r =R)

;

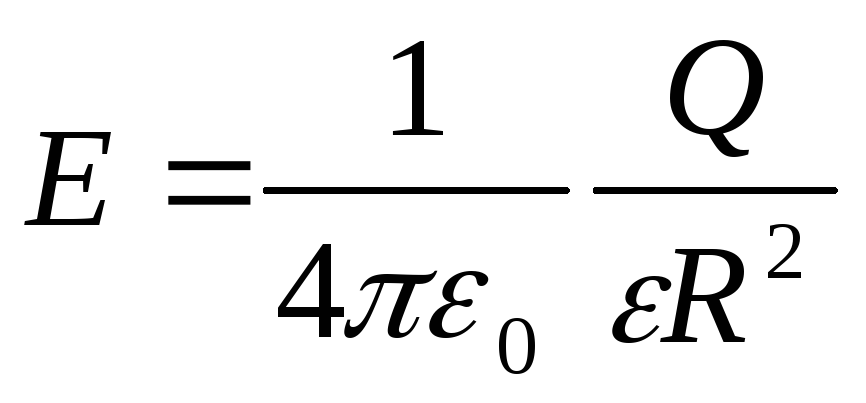в) вне сферы (r>R)

.

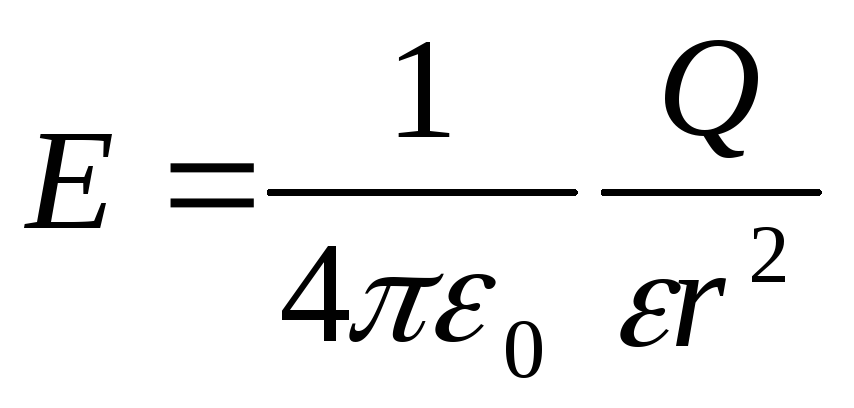 Принцип суперпозиции (наложения) электрических полей, согласно которому напряженность Е результирующего поля, созданного двумя (и более) точечными зарядами, равна векторной (геометрической) сумме напряженностей складываемых полей:

Е =E 1 +Е 2 +...+Е n .

В случае двух электрических полей с напряженностями Е 1 и Е 2 модуль вектора напряженности

где - угол между векторами E 1 и E 2 .

 Напряженность поля, создаваемого бесконечно длинной равномерно заряженной нитью (или цилиндром) нарасстоянииr от ее оси,

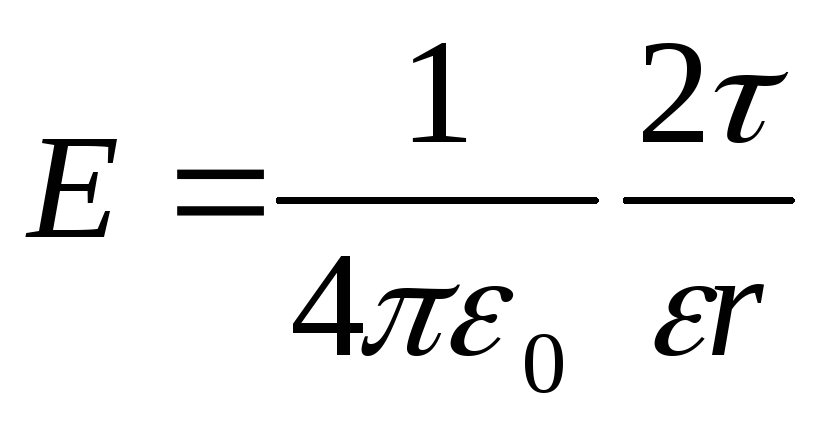, где- линейная плотность заряда.

Линейная плотность заряда есть величина, равная отношению заряда, распределенного по нити, к длине нити (цилиндра):

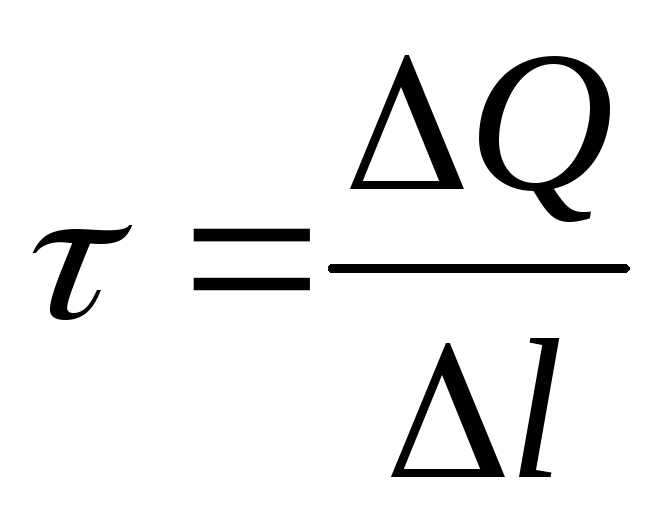
 Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью,

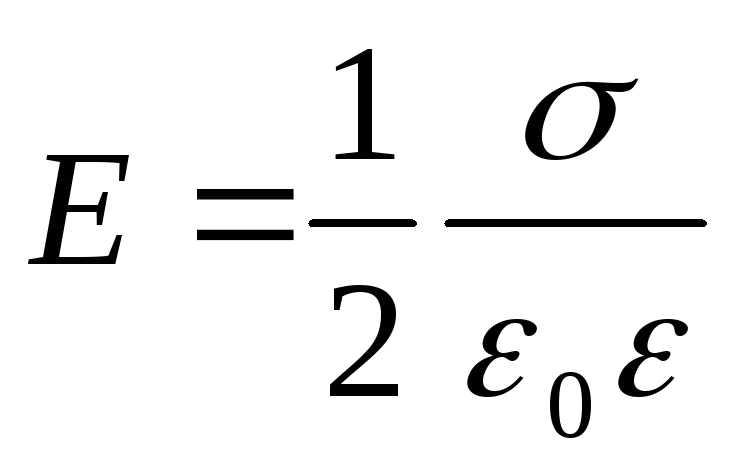
где - поверхностная плотность заряда.

Поверхностная плотность заряда есть величина, равная отношению заряда, распределенного по поверхности, к площади этой поверхности:

.

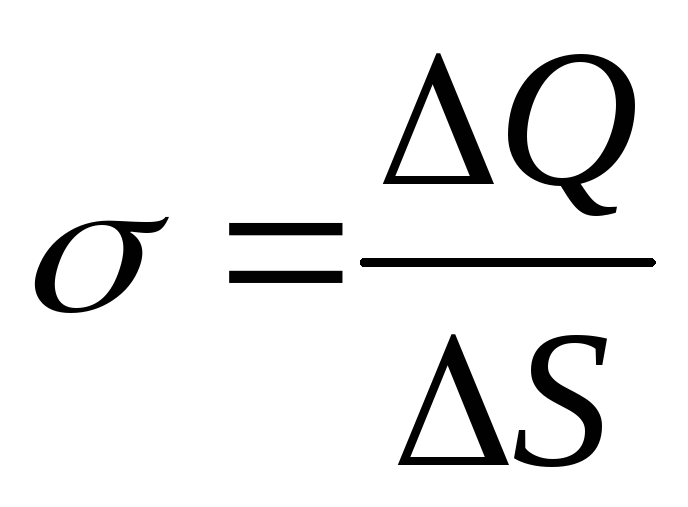 Напряженность поля, создаваемого двумя параллельными бесконечными равномерно и разноименно заряженными плоскостями, с одинаковой по модулю поверхностной плотностью о заряда (поле плоского конденсатора)

.

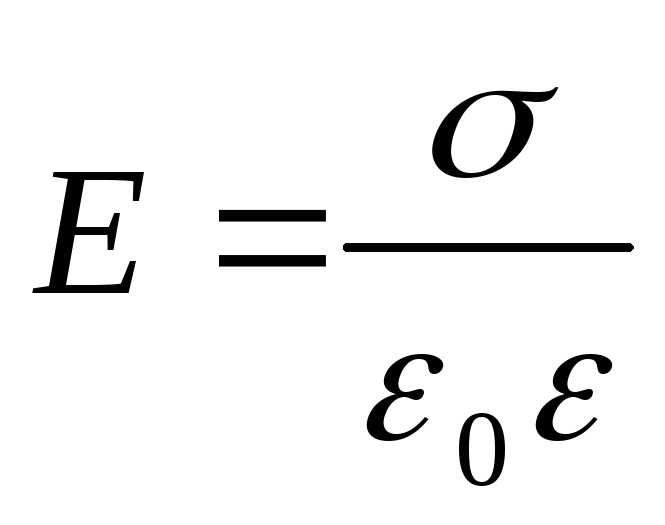Приведенная формула справедлива для вычисления напряженности поля между пластинами плоского конденсатора (в средней части его)только в том случае, если расстояние между пластинами много меньше линейных размеров пластин конденсатора.

 Электрическое смещение D связано с напряженностьюE электрического поля соотношением

D = 0 E .

Это соотношение справедливо только дляизотропных диэлектриков.

 Поток вектора электрического смещения выражается аналогично потоку вектора напряженности электрического поля:

а) в случае однородного поля поток сквозь плоскую поверхность

;

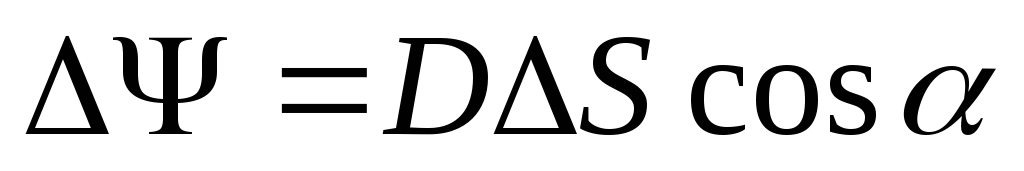б) в случае неоднородного поля и произвольной поверхности

,

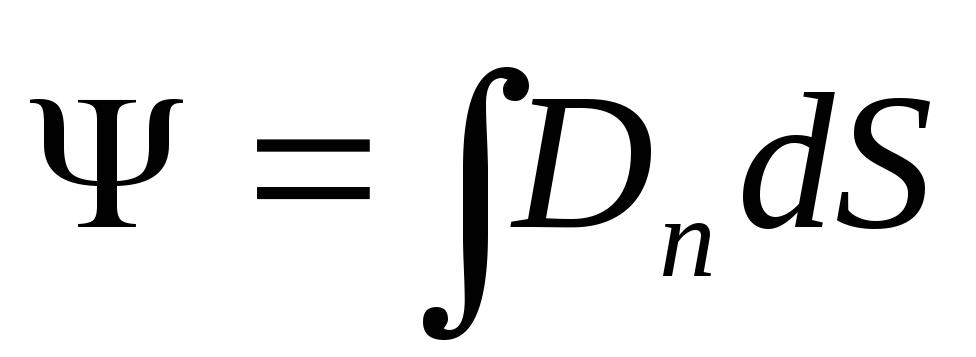где D n - проекция вектораD на направление нормали к элементу поверхности, площадь которой равнаdS .

 Теорема Остроградского - Гаусса. Поток вектора электрического смещения сквозь любую замкнутую поверхность, охватывающую заряды Q 1 ,Q 2 , ...,Q n ,

,

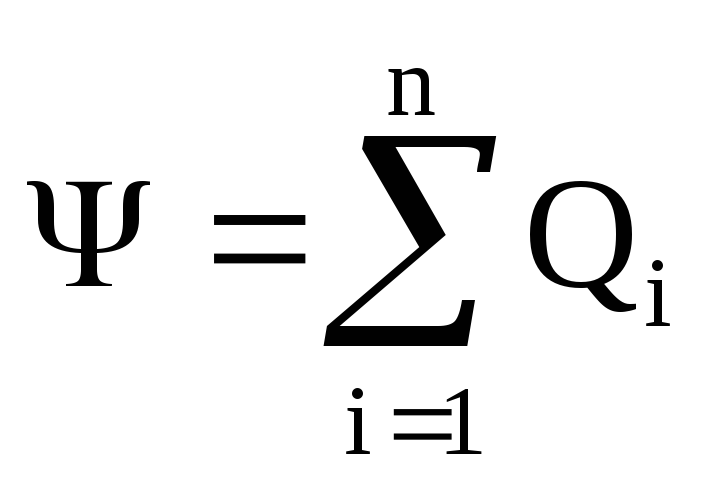где п -число зарядов (со своим знаком), заключенных внутри замкнутой поверхности.

 Циркуляция вектора напряженности электрического поля есть величина, численно равная работе по перемещению единичного точечного положительного заряда вдоль замкнутого контура. Циркуляция выражается интегралом по замкнутому контуру

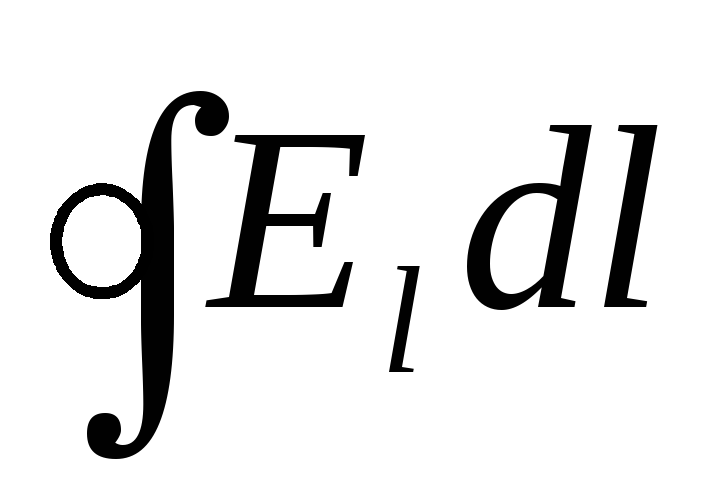,где E l - проекция вектора напряженности Е в данной точке контура на направление касательной к контуру в той же точке.

В случае электростатического поля циркуляция вектора напряженности равна нулю:

.

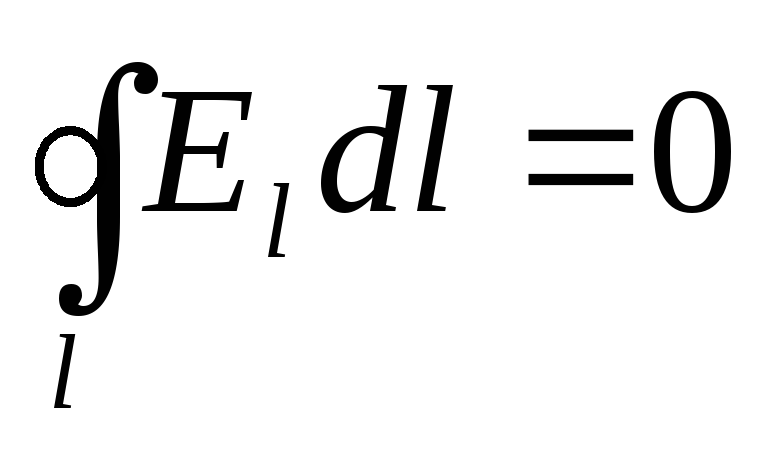Примеры решения задач

П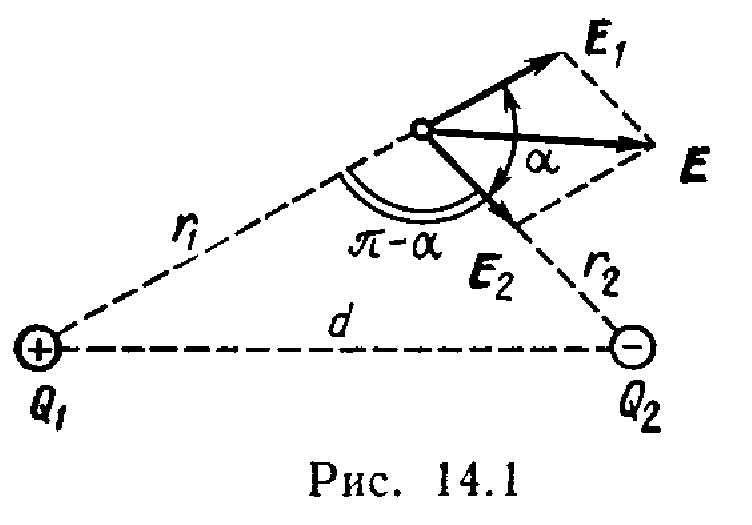

ример 1. Электрическое поле создано двумя точечными зарядами: Q 1 =30нКл и Q 2 = –10 нКл. Расстояние d между зарядами равно 20 см. Определить напряженность электрического поля в точке, находящейся на расстоянииr 1 =15см от первого и на расстоянииr 2 =10 см от второго зарядов.

Решение. Согласно принципу суперпозиции электрических полей, каждый заряд создает поле независимо от присутствия в пространстве других зарядов. Поэтому напряженностьЕ электрического поля в искомой точке может быть найдена как векторная сумма напряженностейE 1 иЕ 2 полей, создаваемых каждым зарядом в отдельности: E =E 1 +E 2 .

Напряженности электрического поля, создаваемого в вакууме первым и вторым зарядами, соответственно равны

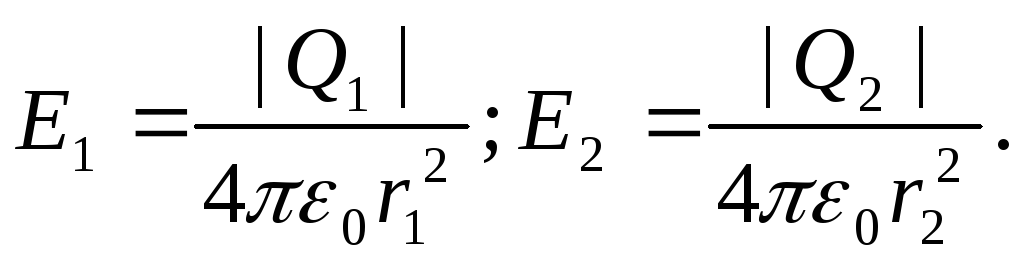(1)

Вектор E 1 (рис. 14.1) направлен по силовой линии от зарядаQ 1 , так как заряд Q 1 >0;векторЕ 2 направлен также по силовой линии, но к заряду Q 2 ,так как Q 2 <0.

Модуль вектора Е найдем по теореме косинусов:

где угол может быть найден из треугольника со сторонами r 1 , r 2 иd:

.

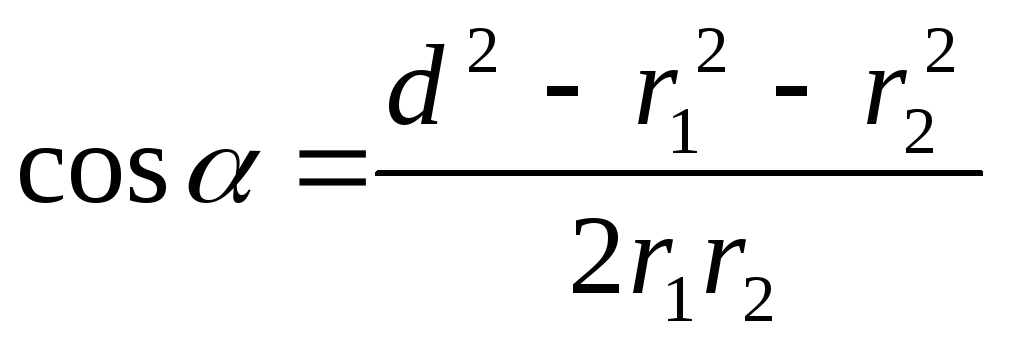В данном случае во избежание громоздких записей вычислим отдельно значение cos.По этой формуле найдем

Подставляя выражения E 1 иE 2 а по формулам (1) в равенство (2) и вынося общий множитель 1/(4 0 ) за знак корня, получаем

.

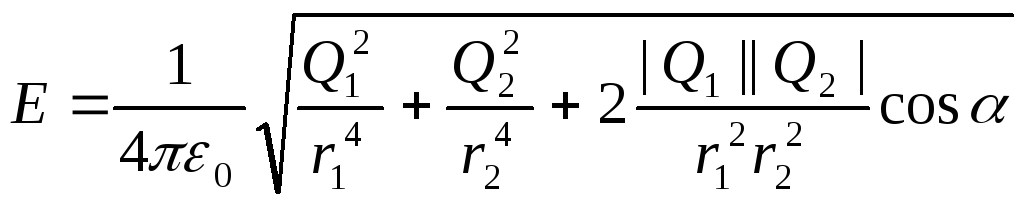Подставив значения величин ,  0 , Q 1 , Q 2 , r 1 -,r 2 ив последнюю формулу и произведя вычисления, найдем

Пример 2. Электрическое поле создано двумя параллельными бесконечными заряженными плоскостями с поверхностными плотностями заряда  1 =0,4мкКл/м 2 и 2 =0,1 мкКл/м 2 . Определить напряженность электрического поля, созданного этими заряженными плоскостями.

Р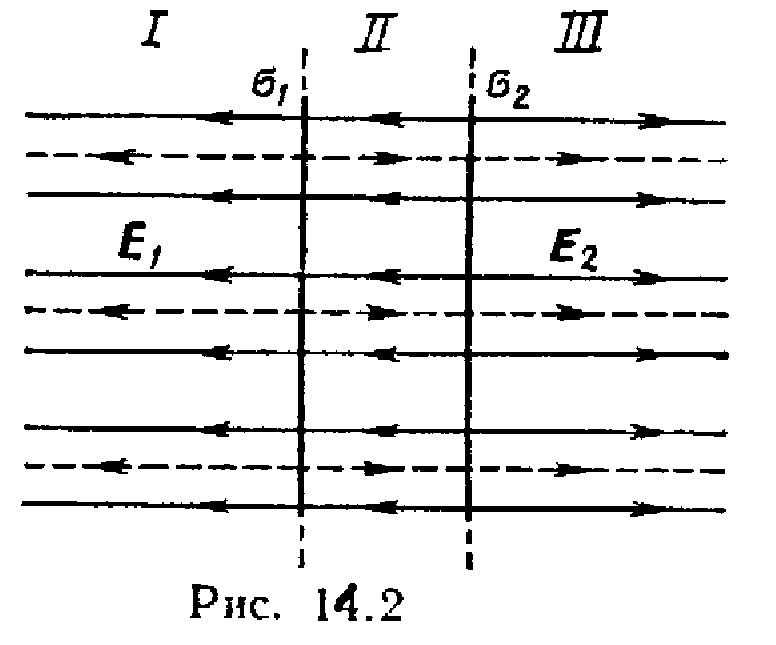

ешение. Согласно принципу суперпозиции, поля, создаваемые каждой заряженной плоскостью в отдельности, накладываются друг на друга, причем каждая заряженная плоскость создает электрическое поле независимо от присутствия другой заряженной плоскости (рис. 14.2).

Напряженности однородных электрических полей, создаваемых первой и второй плоскостями, соответственно равны:

;

.

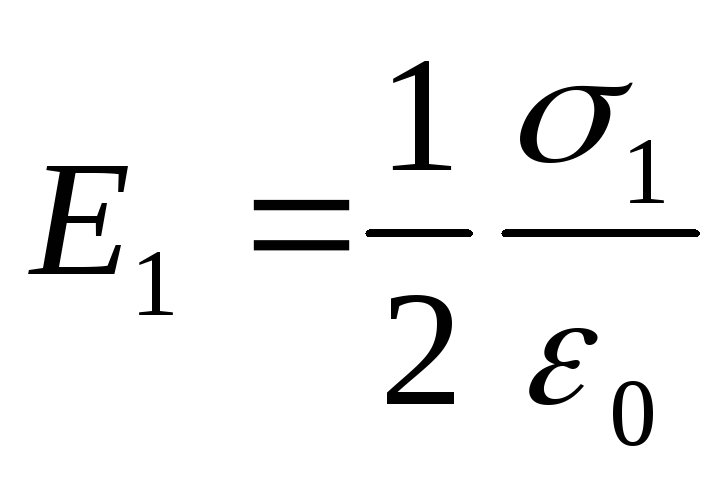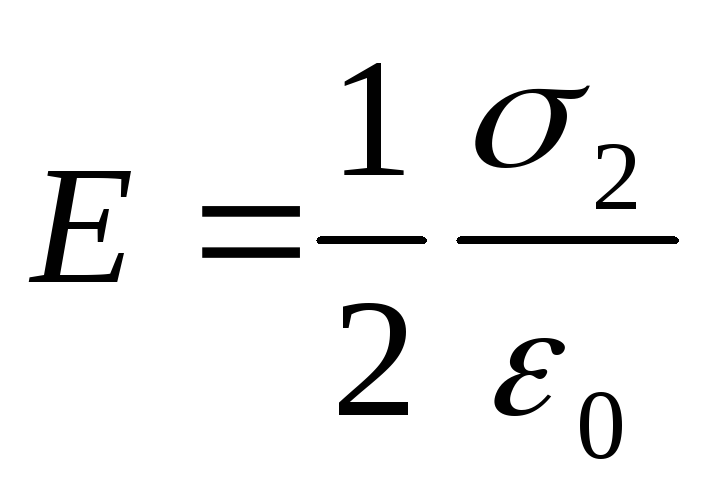Плоскости делят все пространство на три области: I,IIиIII. Как вид но из рисунка, в первой и третьей областях электрические силовые линии обоих полей направлены в одну сторону и, следовательно, напряженности суммарных полейЕ (I) иE (III) в первой и третьей областях равны между собой и равны сумме напряженностей полей, создаваемых первой и второй плоскостями:Е (I) = E (III) =E 1 +E 2 , или

Е (I) = E (III) =

.

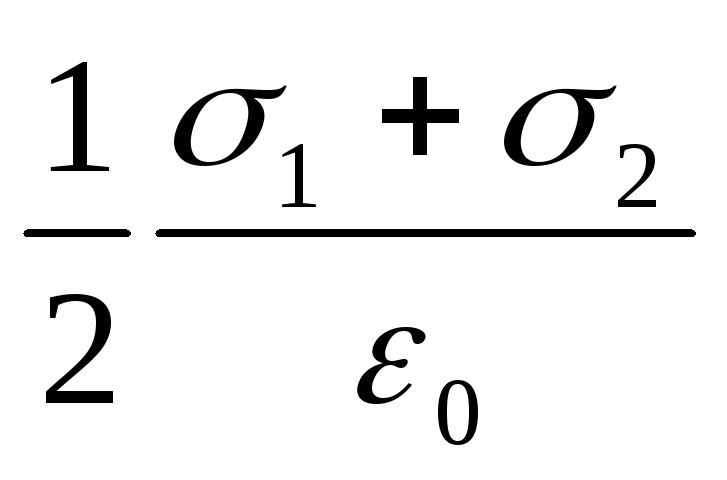Во второй области (между плоскостями) электрические силовые линии полей направлены в противоположные стороны и, следовательно, напряженность поля E (II) равна разности напряженностей полей, создаваемых первой и второй плоскостями: E (II) =|E 1 -E 2 | , или

.

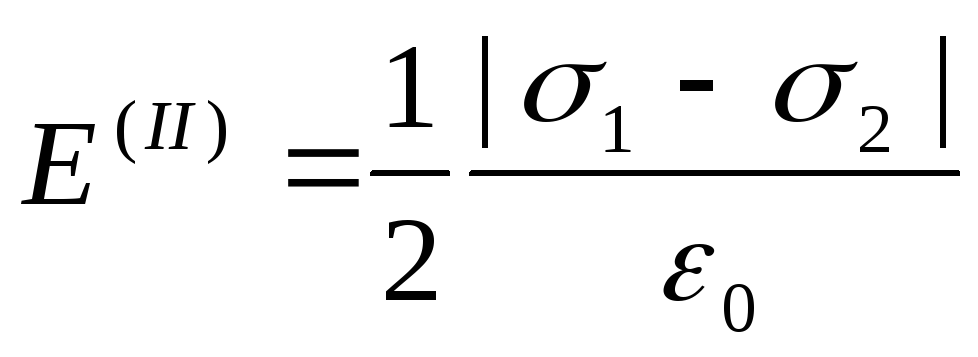Подставив данные и произведя вычисления, получим

E (I) =E (III) =28,3 кВ/м=17 кВ/м.

Картина распределения силовых линий суммарного поля представлена на рис. 14.3.

Пример 3 . На пластинах плоского воздушного конденсатора находится заряд Q =10нКл. Площадь S каждой пластины конденсатора равна 100 см 2 Определить силу F, с которой притягиваются пластины. Поле между пластинами считать однородным.

Решение. Заряд Q одной пластины находится в поле, созданном зарядом другой пластины конденсатора. Следовательно, на первый заряд действует сила (рис. 14.4)

F=E 1 Q, (1)

где E 1 - напряженность поля, создаваемого зарядом одной пластины. Но

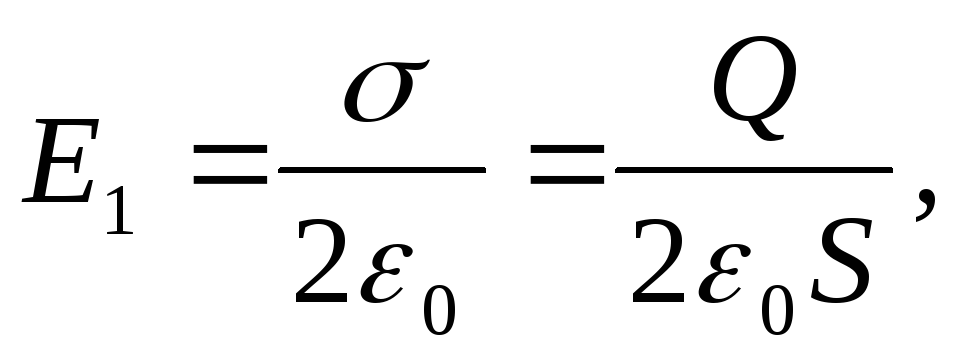где– поверхностная плотность заряда пластины.

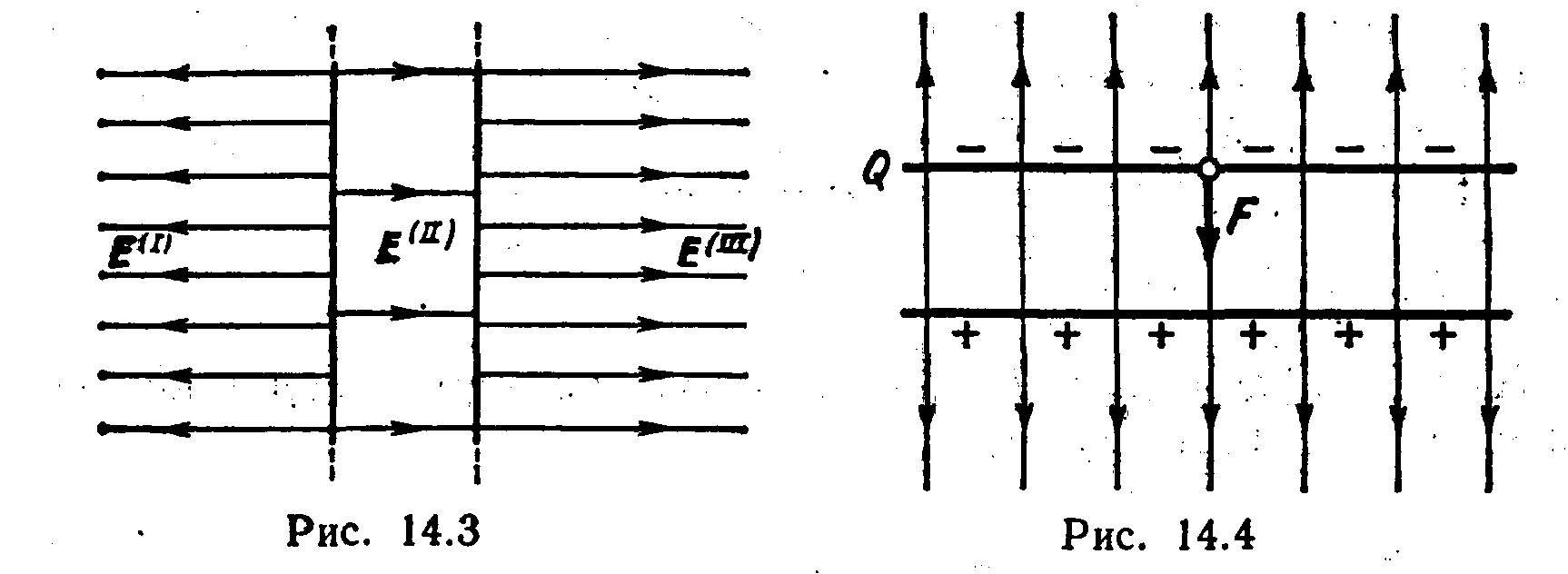
Формула (1) с учетом выражения для E 1 примет вид

F =Q 2 /(2 0 S ).

Подставив значения величин Q , 0 иS в эту формулу и произведя вычисления, получим

F =565мкН.

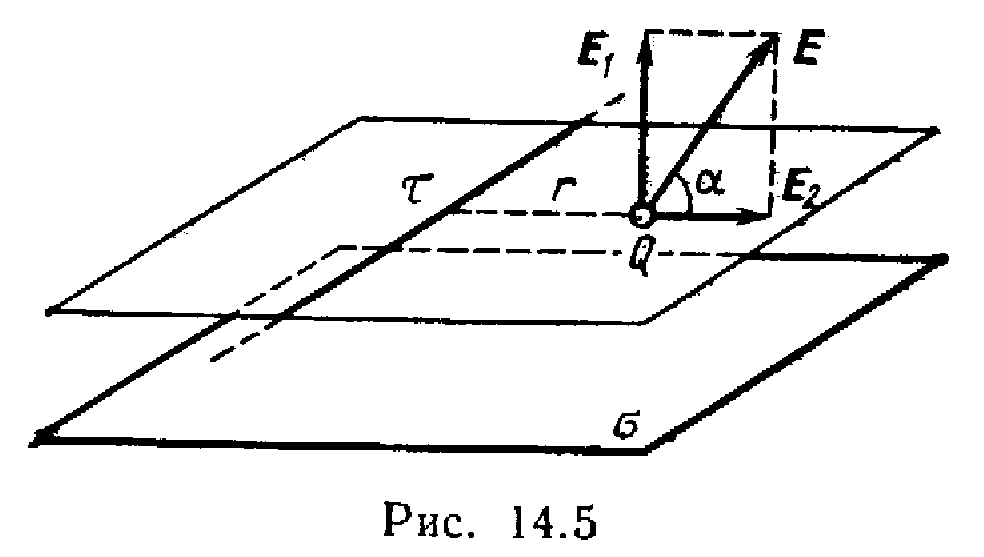
Пример 4. Электрическое поле создано, бесконечной плоскостью, заряженной с поверхностной плотностью= 400 нКл/м 2 , и бесконечной прямой нитью, заряженной с линейной плотностью=100 нКл/м. На расстоянииr =10 см от нити находится точечный заряд Q =10 нКл. Определить силу, действующую на заряд, ее направление, если заряд и нить лежат в одной плоскости, параллельной заряженной плоскости.

Решение. Сила, действующая на заряд, помещённый в поле,

F=EQ , (1)

где Е - Q .

Определим напряженность Е поля, создаваемого, по условию задачи, бесконечной заряженной плоскостью и бесконечной заряженной нитью. Поле, создаваемое бесконечной заряженной плоскостью, однородно, и его напряженность в любой точке

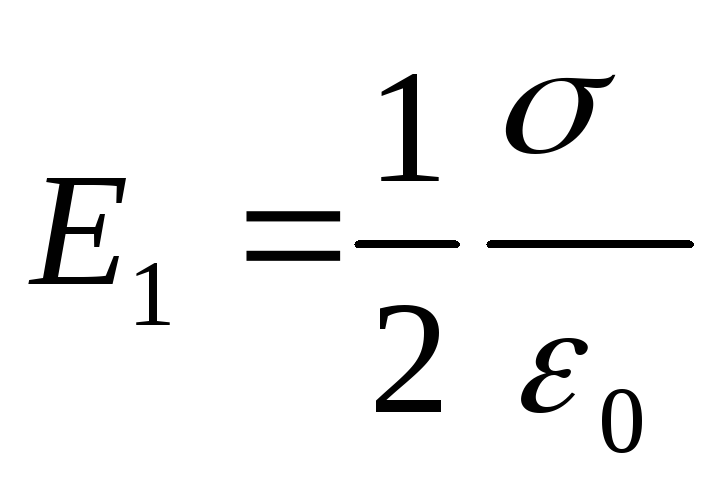. (2)

Поле, создаваемое бесконечной заряженной линией, неоднородно. Его напряженность зависит от расстояния и определяется по формуле

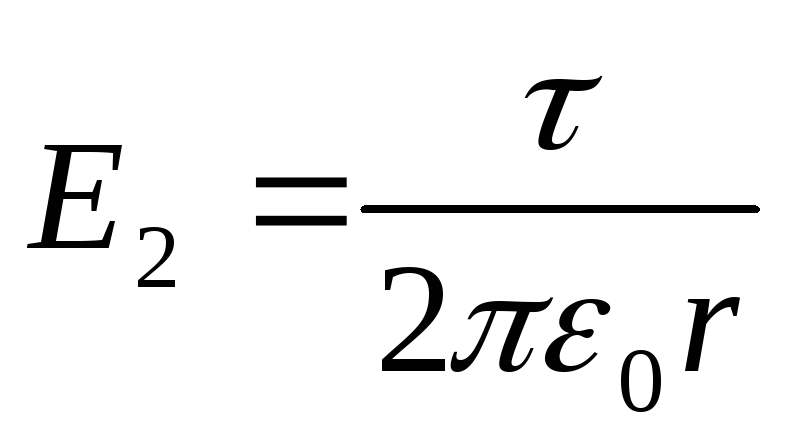. (3)

Согласно принципу суперпозиции электрических полей, напряженность поля в точке, где находится заряд Q ,равна векторной сумме напряженностей E 1 иЕ 2 (рис. 14.5): E =E 1 +E 2 .Так как векторы E 1 иЕ 2 взаимно перпендикулярны, то

.

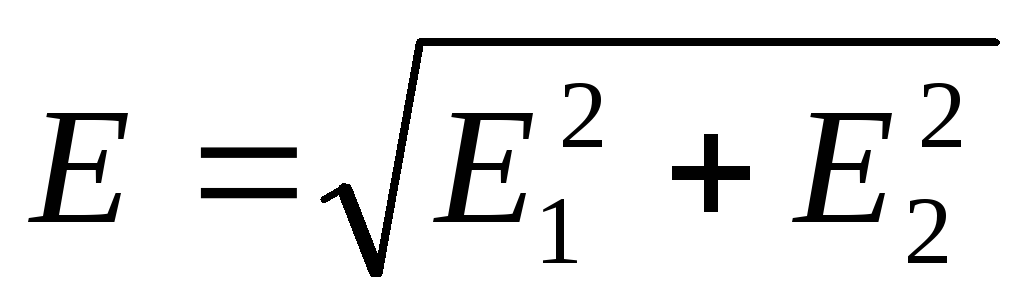Подставляя выражения E 1 иE 2 по формулам (2) и (3) в это равенство, получим

,

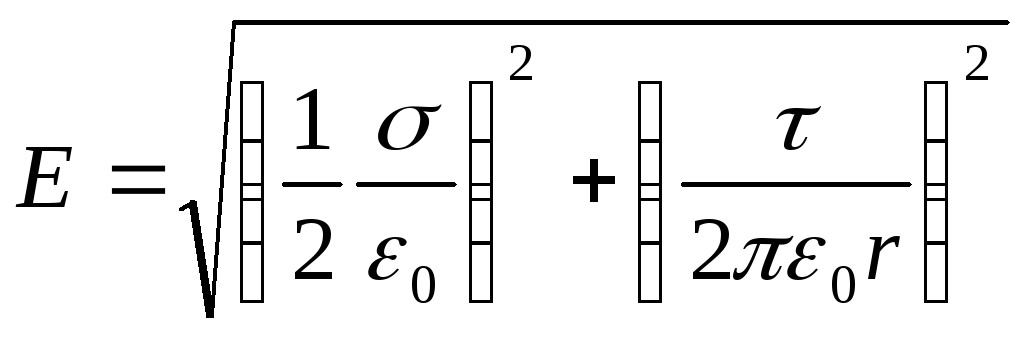или

.

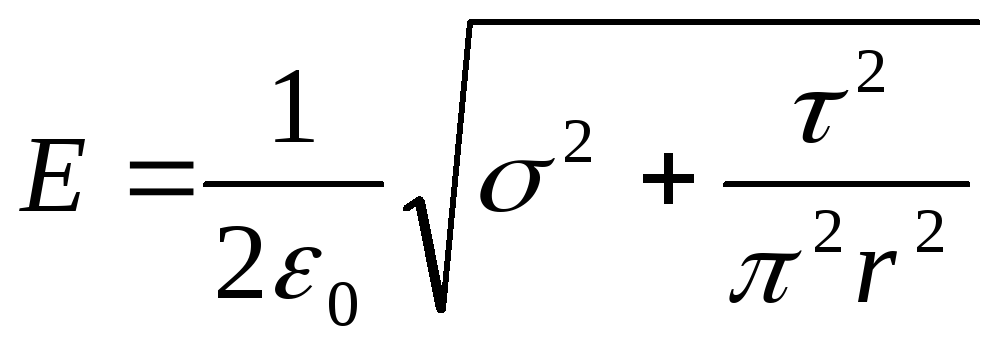Теперь найдем силу F, действующую на заряд, подставив выражениеЕ в формулу (1):

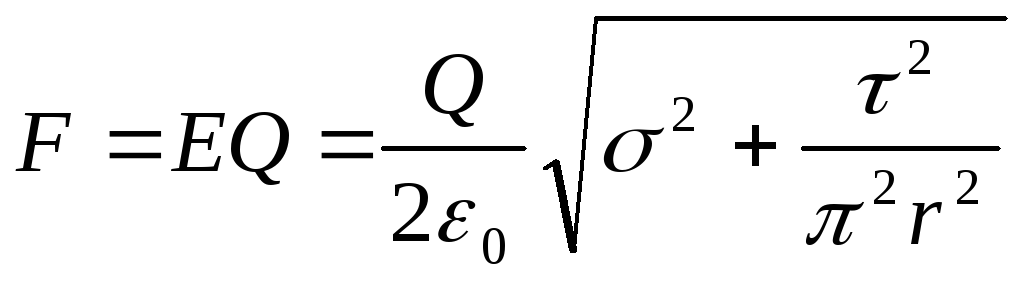. (4)

Подставив значения величин Q , 0 ,,,и r в формулу (4) и сделав вычисления, найдем

F =289мкН.

Направление силы F, действующей на положительный зарядQ , совпадает с направлением вектора напряженностиЕ поля. Направление же вектораЕ задается угломк заряженной плоскости. Из рис. 14.5 следует, что

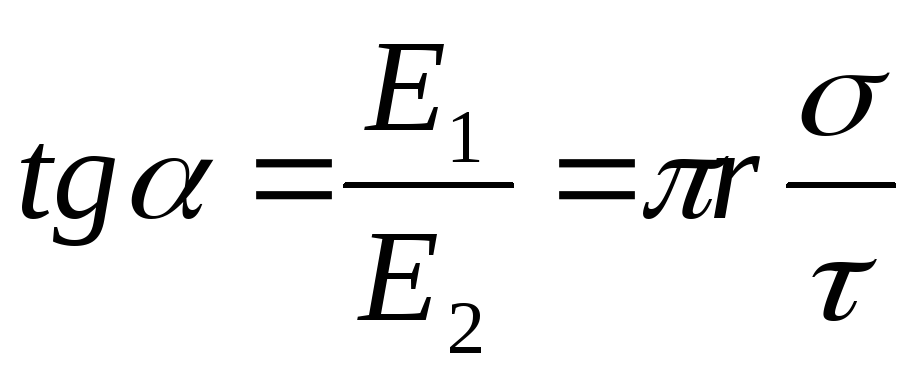, откуда

.

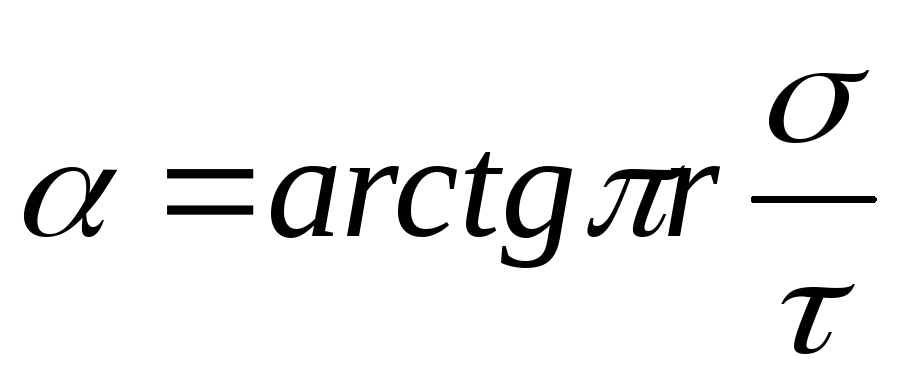Подставив значения величин ,r ,ив это выражение и вычислив, получим

Пример 5. Точечный заряд Q =25нКл находится в ноле, созданном прямым бесконечным цилиндром радиусом R= 1см, равномерно заряженным с поверхностной плотностью=2 мкКл/м 2 . Определить силу, действующую на заряд, помещенный от оси цилиндра на расстоянииr =10 см.

Решение. Сила, действующая на зарядQ , находящийся в поле,

F=QE, (1)

где Е - напряженность поля в точке, в которой находится зарядQ .

Как известно, напряженность поля бесконечно длинного равномерно заряженного цилиндра

E =/(2 0 r ), (2)

где  - линейная плотность заряда.

Выразим линейную плотность через поверхностную плотность. Для этого выделим элемент цилиндра длинойl и выразим находящийся на нем заряд Q 1 двумя, способами:

Q 1 =  S=  2  Rl и Q 1 =l .

Приравняв правые части этих равенств, получим l =2Rl  . После сокращения наl найдем=2R  . С учетом этого формула (2) примет вид E=R  /( 0 r). Подставив это выражениеЕ в формулу (1), найдем искомую силу:

F=Q  R/( 0 r). (3)

Так как R иr входят в формулу в виде отношения, то они могут быть выражены в любых, но только одинаковых единицах.

Выполнив вычисления по формуле (3), найдем

F =2510 -9 210 -6 10 -2 /(8,8510 -12 1010 -2)H==56510 -6 H=565мкH.

Направление силы F совпадает с направлением вектора напряженности Е, а последний в силу симметрии (цилиндр бесконечно длинный) направлен перпендикулярно цилиндру.

Пример 6. Электрическое поле создано тонкой бесконечно длинной нитью, равномерно заряженной с линейной плотностью=30 нКл/м. На расстоянииа =20 см от нити находится плоская круглая площадка радиусомr =1 см. Определить поток вектора напряженности через эту площадку, если плоскость ее составляет угол=30° с линией напряженности, проходящей через середину площадки.

Решение. Поле, создаваемое бесконечно равномерно, заряженной нитью, является неоднородным. Поток вектора напряженности в этом случае выражается интегралом

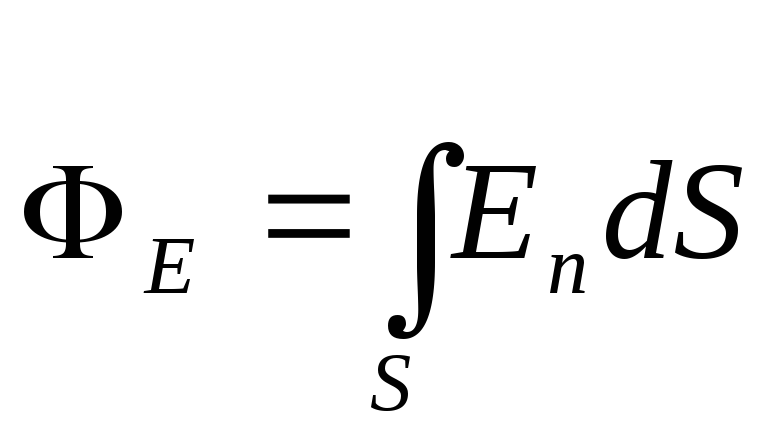, (1)

где E n - проекция вектораЕ на нормальn к поверхности площадки dS. Интегрирование выполняется по всей поверхности площадки, которую пронизывают линии напряженности.

П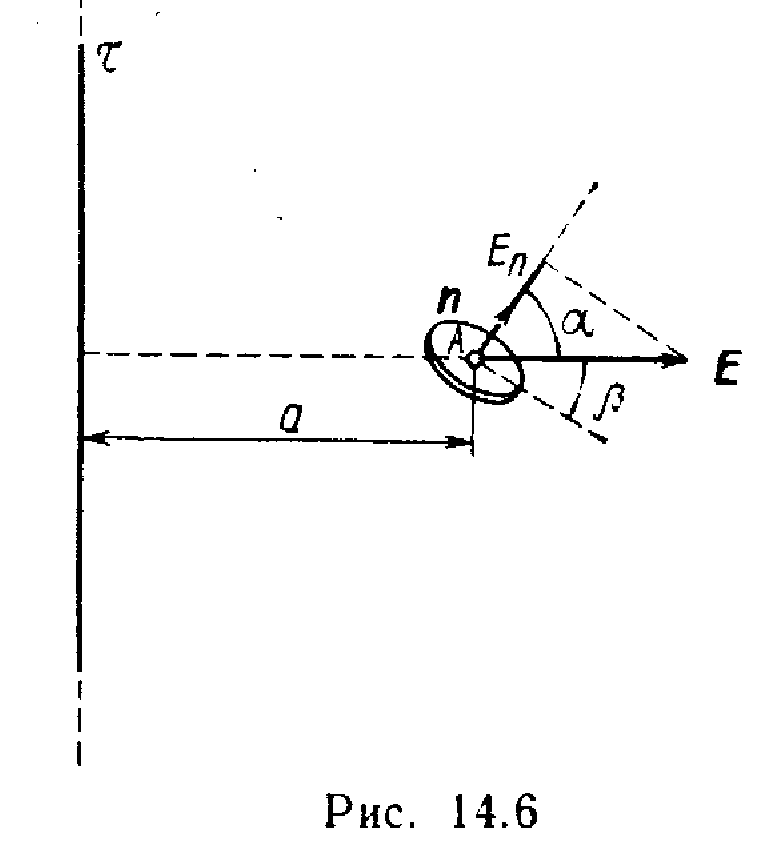

роекцияЕ п вектора напряженности равна, как видно из рис. 14.6,

Е п =Е cos,

где - угол между направлением вектора и нормальюn . С учетом этого формула (1) примет вид

.

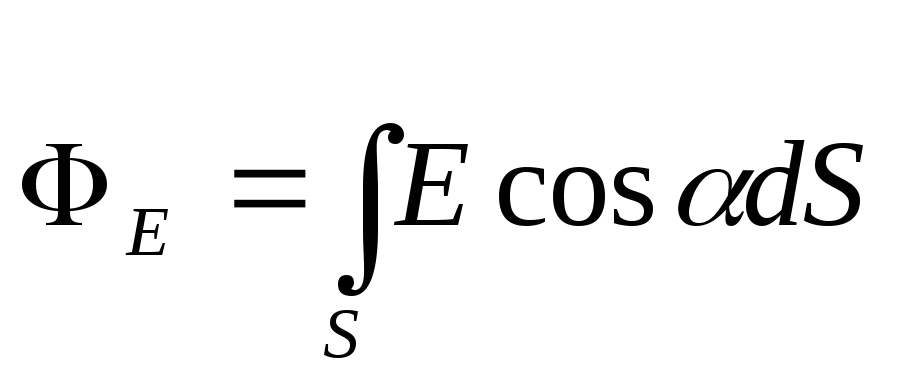Так как размеры поверхности площадки малы по сравнению с расстоянием до нити (r<Е очень мало. меняется по модулю и направлению в пределах площадки, что позволяет заменить под знаком интеграла значенияЕ и cos их средними значениями<E > и и вынести их за знак интеграла:

Выполняя интегрирование и заменяя <E > и их приближенными значениямиЕ A и cos A , вычисленными для средней точки площадки, получим

Ф E =Е A cos A S =r 2 Е A cos A . (2)

Напряженность Е A вычисляется по формулеE A =/(2 0 a) . Из

рис. 14.6 следует cos A =cos(/2-  )=sin.

С учетом выражения Е A и cos A равенство (2.) примет вид

.

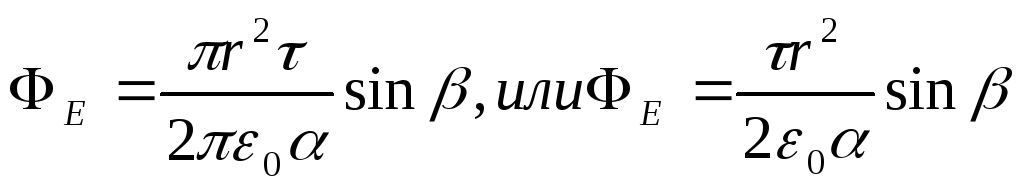Подставив в последнюю формулу данные и произведя вычисления, найдем

Ф E =424 мВ.м.

Пример 7 . Две концентрические проводящие сферы радиусами R 1 =6см и R 2 = 10см несут соответственно заряды Q 1 =lнКл и Q 2 =–0,5 нКл. Найти напряженностьЕ поля в точках, отстоящих от центра сфер на расстояниях r 1 =5см,r 2 =9 смr 3 =15см. Построить графикЕ(r ).

Р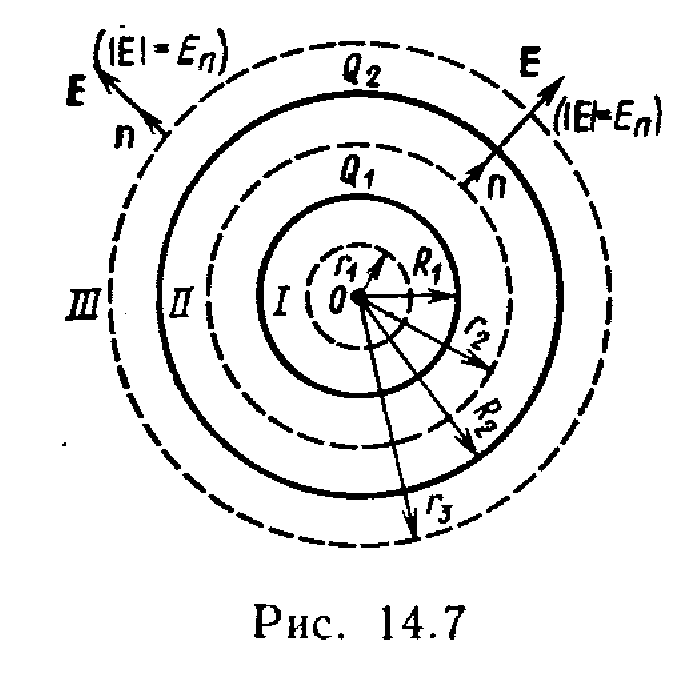

ешение. Заметим, что точки, в которых требуется найти напряженности электрического поля, лежат в трех областях (рис. 14.7): областьI (r <R 1 ), областьII(R 1 <r 2 <R 2 ), областьIII (r 3 >R 2 ).

1. Для определения напряженности E 1 в областиIпроведем сферическую поверхность S 1 радиусом r 1 и воспользуемся теоремой Остроградского-Гаусса. Так как внутри областиIзарядов нет, то согласно указанной теореме получим равенство

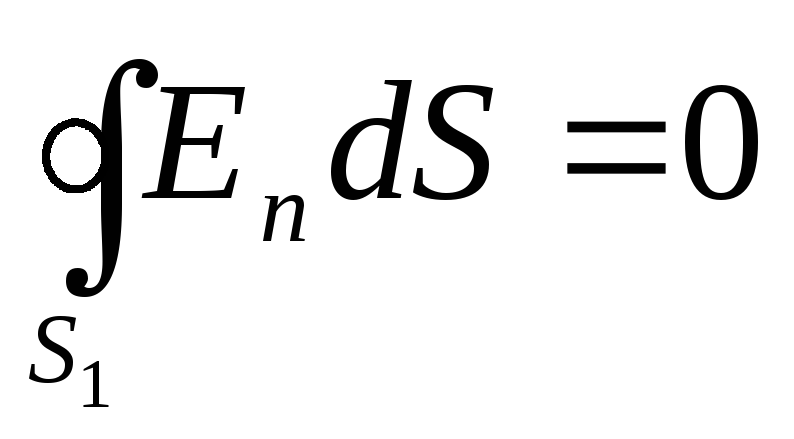, (1)

где E n - нормальная составляющая напряженности электрического поля.

Из соображений симметрии нормальная составляющая E n должна быть равна самой напряженности и постоянна для всех точек сферы, т. е. En=E 1 = const.Поэтому ее можно вынести за знак интеграла. Равенство (1) примет вид

.

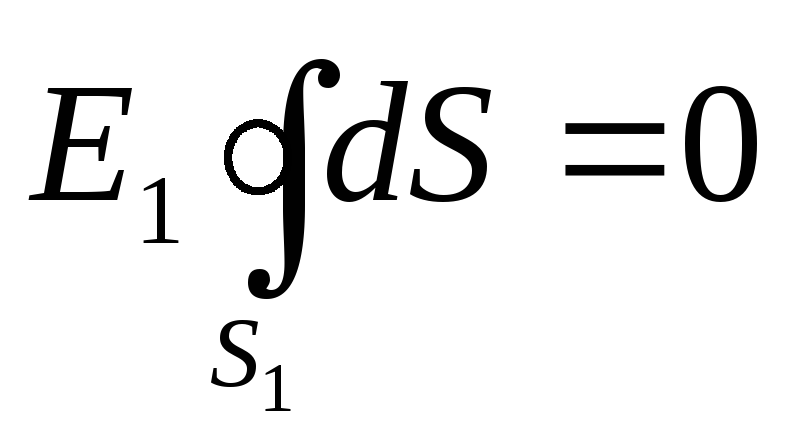Так как площадь сферы не равна нулю, то

E 1 =0,

т. е. напряженность поля во всех точках, удовлетворяющих условию r 1 <.R 1 , будет равна нулю.

2. В области IIсферическую поверхность проведем радиусом r 2 .Так как внутри этой поверхности находится, заряд Q 1 ,тодля нее, согласно теореме Остроградского-Гаусса,можно записать равенство

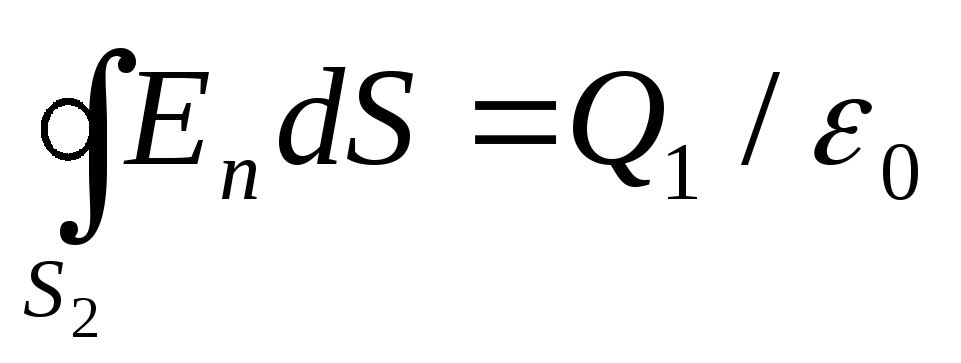. (2)

Так как E n =E 2 =const,то из условий симметрии следует

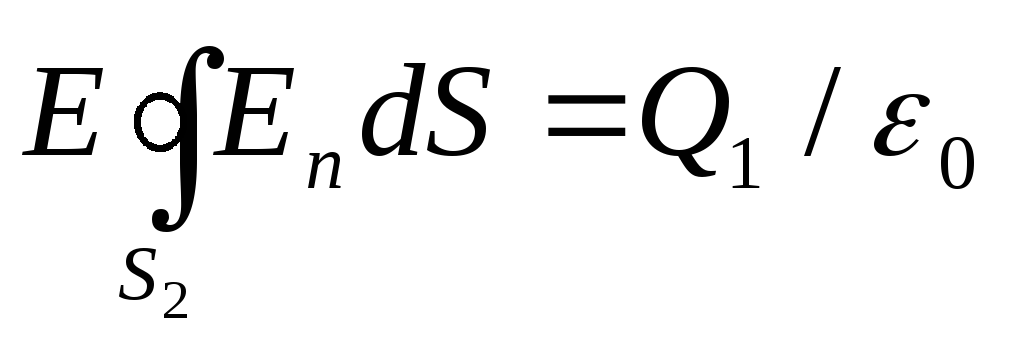, или ES 2 =Q 1 / 0 ,

E 2 =Q 1 /( 0 S 2 ).

Подставив сюда выражение площади сферы, получим

E 2 =Q /(4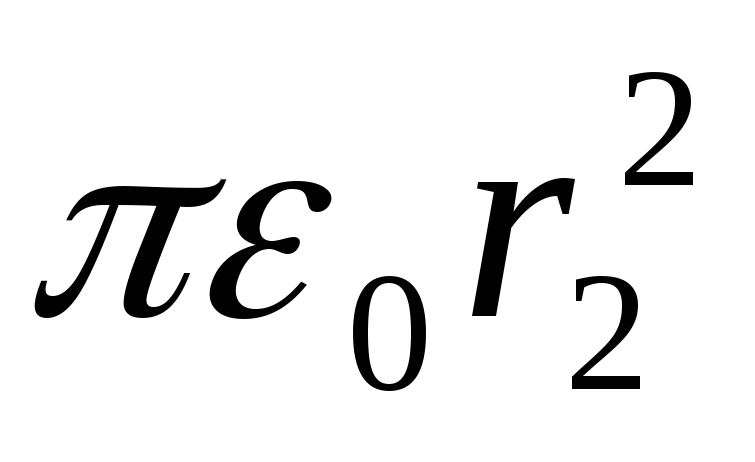

). (3)

3. В области III сферическую поверхность проведем радиусом r 3 . Эта поверхность охватывает суммарный заряд Q 1 +Q 2 . Следовательно, для нее уравнение, записанное на основетеоремыОстроградского - Гаусса, будет иметь вид

.

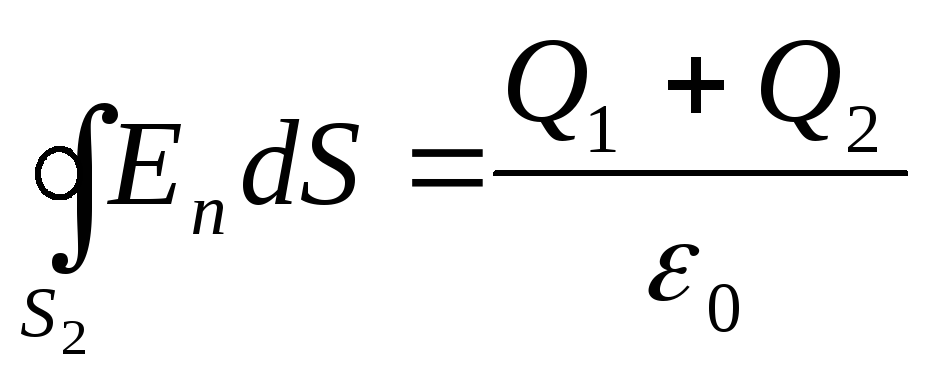Отсюда, использовав положения, примененные в первых двух случаях, найдем

Убедимся в том, что правые части равенств (3) и (4) дают единицу напряженности электрического поля;

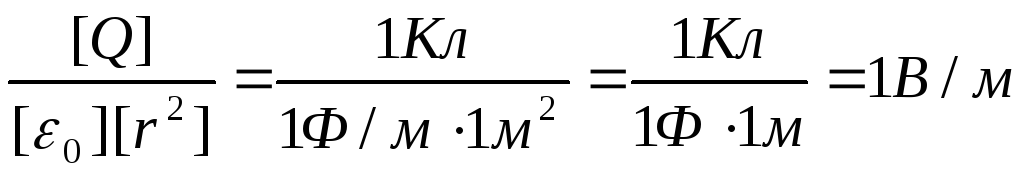
Выразим все величины в единицах СИ (Q 1 =10 -9 Кл, Q 2 = –0,510 -9 Кл, r 1 =0,09м,r 2 =15м, l/(4 0 )=910 9 м/Ф) и произведем вычисления:

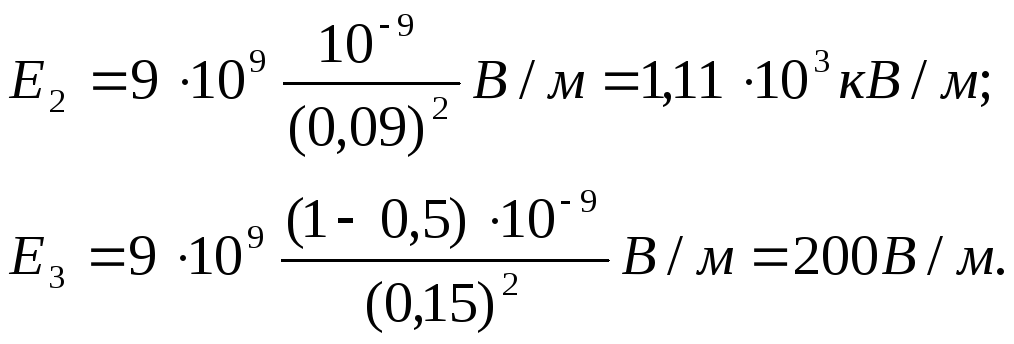
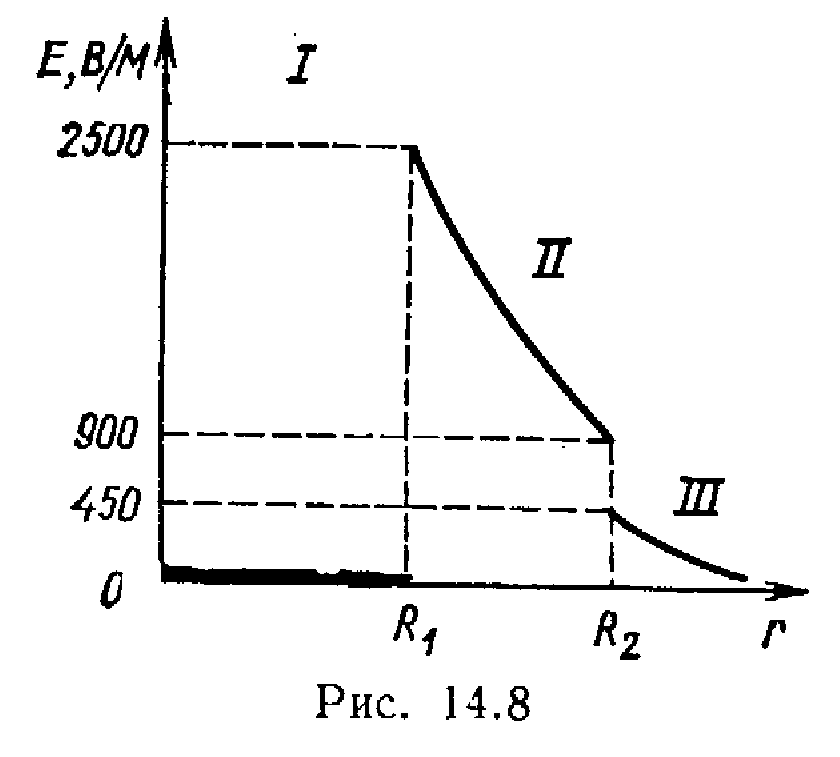
4. Построим график E (r ).В области I (r 1 1 ) напряженностьE =0. В области II (R 1 r<.R 2 ) напряженность E 2 (r )изменяется по закону l/r 2 .В точке r=R 1 напряженность E 2 (R 1 )=Q 1 /(4 0 R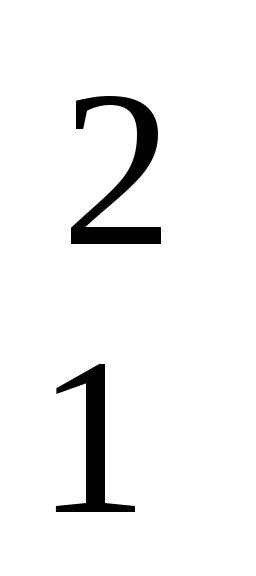)=2500 В/м.В точке r=R 1 (r стремится к R 1 слева) E 2 (R 2 )=Q 1 /(4 0 R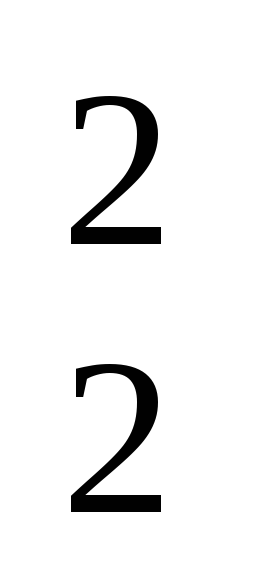)=900В/м. В областиIII(r >R 2 )E 3 (r ) изменяется по закону 1/r 2 , причем в точке r=R 2 (r стремится к R 2 справа)Е 3 (R 2 ) =(Q 1 –|Q 2 |)/(4 0 R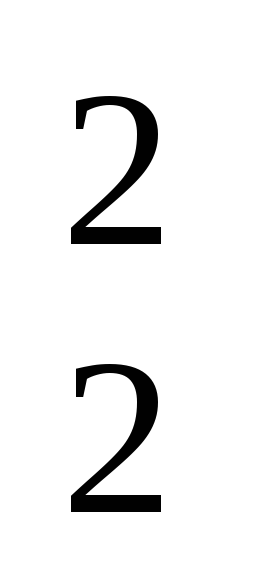)=450 В/м. Таким образом, функцияЕ (r ) в точкахr =R 1 и r=R 2 терпит разрыв. График зависимостиЕ(r ) представлен на рис. 14.8.

Задачи

Напряженность поля точечных зарядов

14.1. Определить напряженностьЕ электрического поля, создаваемого точечным зарядом Q =10 нКл на расстоянииr =10 см от него. Диэлектрик - масло.

14.2. Расстояние d между двумя точечными зарядами Q 1 =+8 нКл и Q 2 = –5,3 нКл равно 40 см. Вычислить напряженностьЕ поля в точке, лежащей посередине между зарядами. Чему равна напряженность, если второй заряд будет положительным?

14.3. Q 1 =10нКл и Q 2 = –20 нКл, находящимися на расстоянии d =20см друг от друга. Определить напряженностьE поля в точке, удаленной от первого заряда на r 1 =30см и от второго наr 2 =50 см.

14.4. Расстояниеd между двумя точечными положительными зарядами Q 1 =9Q и Q 2 =Qравно 8 см. На каком расстоянии г от первого заряда находится точка, в которой напряженностьЕ поля зарядов равна нулю? Где находилась бы эта точка, если бы второй заряд был отрицательным?

14.5. Два точечных заряда Q 1 =2Q и Q 2 = –Q находятся на расстоянииd друг от друга. Найти положение точки на прямой, проходящей через эти заряды, напряженностьЕ поля в которой равна нулю,

14.6. Электрическое поле создано двумя точечными зарядамиQ 1 =40нКл и Q 2 = –10 нКл, находящимися на расстоянииd =10 см друг от друга. Определить напряженностьЕ поля в точке, удаленной от первого заряда на r 1 =12 см и от второго наr 2 =6 см.

Напряженность поля заряда, распределенного по кольцу и сфере

14.7. Тонкое кольцо радиусомR =8 см несет заряд, равномерно распределенный с линейной плотностью=10 нКл/м. Какова напряженностьЕ электрического поля в точке, равноудаленной от всех точек кольца на расстояниеr =10 см?

14.8. Полусфера несет заряд, равномерно распределенный с поверхностной плотностью=1,нКл/м 2 . Найти напряженностьЕ электрического поля в геометрическом центре полусферы.

14.9. На металлической сфере радиусомR =10 см находится заряд Q =lнКл. Определить напряженностьЕ электрического поля в следующих точках: 1) на расстоянииr 1 =8 см от центра сферы; 2) на ее поверхности; 3) на расстоянииr 2 =15 см от центра сферы. Построить график зависимостиE отr .

14.10. Две концентрические металлические заряженные сферы радиусами R 1 =6cм иR 2 =10см несут соответственно заряды Q 1 =1 нКл и Q 2 = – 0,5 нКл. Найти напряженностиЕ поля в точках. отстоящих от центра сфер на расстоянияхr 1 =5 см,r 2 =9 см,r 3 =15 см. Построить график зависимостиЕ(r ).

Напряженность поля заряженной линии

14.11. Очень длинная тонкая прямая проволока несет заряд, равномерно распределенный по всей ее длине. Вычислить линейную плотностьзаряда, если напряженностьE поля на расстоянииа =0,5 м от проволоки против ее середины равна 200 В/м.

14.12. Расстояниеd между двумя длинными тонкими проволоками, расположенными параллельно друг другу, равно 16 см. Проволоки равномерно заряжены разноименными зарядами с линейной плотностью||=^150. мкКл/м. Какова напряженностьЕ поля в точке, удаленной наr =10 см как от первой, так и от второй проволоки?

14.13. Прямой металлический стержень диаметромd =5см и длинойl =4 м несет равномерно распределенный по его поверхности заряд Q =500нКл. Определить напряженностьЕ поля в точке, находящейся против середины стержня на расстоянииа =1 см от его поверхности.

14.14. Бесконечно длинная тонкостенная металлическая трубка радиусом R =2см несет равномерно распределенный по поверхности заряд (=1 нКл/м 2). Определить напряженностьЕ поля в точках, отстоящих от оси трубки на расстояниях r 1 =lсм,r 2 =3 см. Построить график зависимостиЕ(r ).

14.15. Две длинные тонкостенные коаксиальные трубки радиусами R 1 =2см иR 2 =4 см несут заряды, равномерно распределенные по длине с линейными плотностями  1 =lнКл/м и 2 = –0,5 нКл/м. Пространство между трубками заполнено эбонитом. Определить напряженностьЕ поля в точках, находящихся на расстоянияхr 1 =1 см, r 2 =3см,r 3 =5 см от оси трубок; Построить график зависимостиЕ от r .