Problem B9 gives a graph of a function or derivative from which you need to determine one of the following quantities:

1. The value of the derivative at some point x 0,
2. Maximum or minimum points (extremum points),
3. Intervals of increasing and decreasing functions (intervals of monotonicity).

The functions and derivatives presented in this problem are always continuous, making the solution much easier. Despite the fact that the task belongs to the section of mathematical analysis, even the weakest students can do it, since no deep theoretical knowledge is required here.

To find the value of the derivative, extremum points and monotonicity intervals, there are simple and universal algorithms - all of them will be discussed below.

Read the conditions of problem B9 carefully to avoid making stupid mistakes: sometimes you come across quite lengthy texts, but there are few important conditions that affect the course of the solution.

Calculation of the derivative value. Two point method

If the problem is given a graph of a function f(x), tangent to this graph at some point x 0, and it is required to find the value of the derivative at this point, the following algorithm is applied:

1. Find two “adequate” points on the tangent graph: their coordinates must be integer. Let's denote these points as A (x 1 ; y 1) and B (x 2 ; y 2). Write down the coordinates correctly - this is a key point in the solution, and any mistake here will lead to an incorrect answer.
2. Knowing the coordinates, it is easy to calculate the increment of the argument Δx = x 2 − x 1 and the increment of the function Δy = y 2 − y 1 .
3. Finally, we find the value of the derivative D = Δy/Δx. In other words, you need to divide the increment of the function by the increment of the argument - and this will be the answer.

Let us note once again: points A and B must be looked for precisely on the tangent, and not on the graph of the function f(x), as often happens. The tangent line will necessarily contain at least two such points - otherwise the problem will not be formulated correctly.

Consider points A (−3; 2) and B (−1; 6) and find the increments:
Δx = x 2 − x 1 = −1 − (−3) = 2; Δy = y 2 − y 1 = 6 − 2 = 4.

Let's find the value of the derivative: D = Δy/Δx = 4/2 = 2.

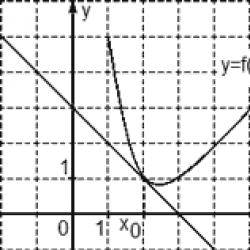
Task. The figure shows a graph of the function y = f(x) and a tangent to it at the point with the abscissa x 0. Find the value of the derivative of the function f(x) at the point x 0 .

Consider points A (0; 3) and B (3; 0), find the increments:
Δx = x 2 − x 1 = 3 − 0 = 3; Δy = y 2 − y 1 = 0 − 3 = −3.

Now we find the value of the derivative: D = Δy/Δx = −3/3 = −1.

Task. The figure shows a graph of the function y = f(x) and a tangent to it at the point with the abscissa x 0. Find the value of the derivative of the function f(x) at the point x 0 .

Consider points A (0; 2) and B (5; 2) and find the increments:
Δx = x 2 − x 1 = 5 − 0 = 5; Δy = y 2 − y 1 = 2 − 2 = 0.

It remains to find the value of the derivative: D = Δy/Δx = 0/5 = 0.

From the last example, we can formulate a rule: if the tangent is parallel to the OX axis, the derivative of the function at the point of tangency is zero. In this case, you don’t even need to count anything - just look at the graph.

Calculation of maximum and minimum points

Sometimes, instead of a graph of a function, Problem B9 gives a graph of the derivative and requires finding the maximum or minimum point of the function. In this situation, the two-point method is useless, but there is another, even simpler algorithm. First, let's define the terminology:

1. The point x 0 is called the maximum point of the function f(x) if in some neighborhood of this point the following inequality holds: f(x 0) ≥ f(x).
2. The point x 0 is called the minimum point of the function f(x) if in some neighborhood of this point the following inequality holds: f(x 0) ≤ f(x).

In order to find the maximum and minimum points from the derivative graph, just follow these steps:

1. Redraw the derivative graph, removing all unnecessary information. As practice shows, unnecessary data only interferes with the decision. Therefore, we mark the zeros of the derivative on the coordinate axis - and that’s it.
2. Find out the signs of the derivative on the intervals between zeros. If for some point x 0 it is known that f'(x 0) ≠ 0, then only two options are possible: f'(x 0) ≥ 0 or f'(x 0) ≤ 0. The sign of the derivative is easy to determine from the original drawing: if the derivative graph lies above the OX axis, then f'(x) ≥ 0. And vice versa, if the derivative graph lies below the OX axis, then f'(x) ≤ 0.
3. We check the zeros and signs of the derivative again. Where the sign changes from minus to plus is the minimum point. Conversely, if the sign of the derivative changes from plus to minus, this is the maximum point. Counting is always done from left to right.

This scheme only works for continuous functions - there are no others in Problem B9.

Task. The figure shows a graph of the derivative of the function f(x) defined on the interval [−5; 5]. Find the minimum point of the function f(x) on this segment.

Let's get rid of unnecessary information and leave only the boundaries [−5; 5] and zeros of the derivative x = −3 and x = 2.5. We also note the signs:

Obviously, at the point x = −3 the sign of the derivative changes from minus to plus. This is the minimum point.

Task. The figure shows a graph of the derivative of the function f(x) defined on the interval [−3; 7]. Find the maximum point of the function f(x) on this segment.

Let's redraw the graph, leaving only the boundaries [−3; 7] and zeros of the derivative x = −1.7 and x = 5. Let us note the signs of the derivative on the resulting graph. We have:

Obviously, at the point x = 5 the sign of the derivative changes from plus to minus - this is the maximum point.

Task. The figure shows a graph of the derivative of the function f(x), defined on the interval [−6; 4]. Find the number of maximum points of the function f(x) belonging to the segment [−4; 3].

From the conditions of the problem it follows that it is enough to consider only the part of the graph limited by the segment [−4; 3]. Therefore, we build a new graph on which we mark only the boundaries [−4; 3] and zeros of the derivative inside it. Namely, points x = −3.5 and x = 2. We get:

On this graph there is only one maximum point x = 2. It is at this point that the sign of the derivative changes from plus to minus.

A small note about points with non-integer coordinates. For example, in the last problem the point x = −3.5 was considered, but with the same success we can take x = −3.4. If the problem is compiled correctly, such changes should not affect the answer, since the points “without a fixed place of residence” do not directly participate in solving the problem. Of course, this trick won’t work with integer points.

Finding intervals of increasing and decreasing functions

In such a problem, like the maximum and minimum points, it is proposed to use the derivative graph to find areas in which the function itself increases or decreases. First, let's define what increasing and decreasing are:

1. A function f(x) is said to be increasing on a segment if for any two points x 1 and x 2 from this segment the following statement is true: x 1 ≤ x 2 ⇒ f(x 1) ≤ f(x 2). In other words, the larger the argument value, the larger the function value.
2. A function f(x) is said to be decreasing on a segment if for any two points x 1 and x 2 from this segment the following statement is true: x 1 ≤ x 2 ⇒ f(x 1) ≥ f(x 2). Those. A larger argument value corresponds to a smaller function value.

Let us formulate sufficient conditions for increasing and decreasing:

1. In order for a continuous function f(x) to increase on the segment , it is sufficient that its derivative inside the segment be positive, i.e. f’(x) ≥ 0.
2. In order for a continuous function f(x) to decrease on the segment , it is sufficient that its derivative inside the segment be negative, i.e. f’(x) ≤ 0.

Let us accept these statements without evidence. Thus, we obtain a scheme for finding intervals of increasing and decreasing, which is in many ways similar to the algorithm for calculating extremum points:

1. Remove all unnecessary information. In the original graph of the derivative, we are primarily interested in the zeros of the function, so we will leave only them.
2. Mark the signs of the derivative at the intervals between zeros. Where f’(x) ≥ 0, the function increases, and where f’(x) ≤ 0, it decreases. If the problem sets restrictions on the variable x, we additionally mark them on a new graph.
3. Now that we know the behavior of the function and the constraints, it remains to calculate the quantity required in the problem.

Task. The figure shows a graph of the derivative of the function f(x) defined on the interval [−3; 7.5]. Find the intervals of decrease of the function f(x). In your answer, indicate the sum of the integers included in these intervals.

As usual, let's redraw the graph and mark the boundaries [−3; 7.5], as well as zeros of the derivative x = −1.5 and x = 5.3. Then we note the signs of the derivative. We have:

Since the derivative is negative on the interval (− 1.5), this is the interval of decreasing function. It remains to sum all the integers that are inside this interval:
−1 + 0 + 1 + 2 + 3 + 4 + 5 = 14.

Task. The figure shows a graph of the derivative of the function f(x), defined on the interval [−10; 4]. Find the intervals of increase of the function f(x). In your answer, indicate the length of the largest of them.

Let's get rid of unnecessary information. Let us leave only the boundaries [−10; 4] and zeros of the derivative, of which there were four this time: x = −8, x = −6, x = −3 and x = 2. Let’s mark the signs of the derivative and get the following picture:

We are interested in the intervals of increasing function, i.e. such where f’(x) ≥ 0. There are two such intervals on the graph: (−8; −6) and (−3; 2). Let's calculate their lengths:
l 1 = − 6 − (−8) = 2;
l 2 = 2 − (−3) = 5.

Since we need to find the length of the largest of the intervals, we write down the value l 2 = 5 as an answer.

Showing the connection between the sign of the derivative and the nature of the monotonicity of the function.

Please be extremely careful about the following. Look, the schedule of WHAT is given to you! Function or its derivative

If given a graph of the derivative, then we will be interested only in the function signs and zeros. We are not interested in any “hills” or “hollows” in principle!

Task 1.

The figure shows a graph of a function defined on the interval. Determine the number of integer points at which the derivative of the function is negative.

Solution:

In the figure, the areas of decreasing function are highlighted in color:

These decreasing regions of the function contain 4 integer values.

Task 2.

The figure shows a graph of a function defined on the interval. Find the number of points at which the tangent to the graph of the function is parallel to or coincides with the line.

Solution:

Once the tangent to the graph of a function is parallel (or coincides) with a straight line (or, which is the same thing), having slope, equal to zero, then the tangent has an angular coefficient .

This in turn means that the tangent is parallel to the axis, since the slope is the tangent of the angle of inclination of the tangent to the axis.

Therefore, we find extremum points (maximum and minimum points) on the graph - it is at these points that the functions tangent to the graph will be parallel to the axis.

There are 4 such points.

Task 3.

The figure shows a graph of the derivative of a function defined on the interval. Find the number of points at which the tangent to the graph of the function is parallel to or coincides with the line.

Solution:

Since the tangent to the graph of a function is parallel (or coincides) with a line that has an slope, then the tangent also has a slope.

This in turn means that at the touch points.

Therefore, we look at how many points on the graph have an ordinate equal to .

As you can see, there are four such points.

Task 4.

The figure shows a graph of a function defined on the interval. Find the number of points at which the derivative of the function is 0.

Solution:

The derivative is equal to zero at extremum points. We have 4 of them:

Task 5.

The figure shows a graph of a function and eleven points on the x-axis:. At how many of these points is the derivative of the function negative?

Solution:

On intervals of decreasing function, its derivative takes negative values. And the function decreases at points. There are 4 such points.

Task 6.

The figure shows a graph of a function defined on the interval. Find the sum of the extremum points of the function.

Solution:

Extremum points– these are the maximum points (-3, -1, 1) and minimum points (-2, 0, 3).

Sum of extremum points: -3-1+1-2+0+3=-2.

Task 7.

The figure shows a graph of the derivative of a function defined on the interval. Find the intervals of increase of the function. In your answer, indicate the sum of integer points included in these intervals.

Solution:

The figure highlights the intervals where the derivative of the function is non-negative.

There are no integer points on the small increasing interval; on the increasing interval there are four integer values: , , and .

Their sum:

Task 8.

The figure shows a graph of the derivative of a function defined on the interval. Find the intervals of increase of the function. In your answer, indicate the length of the largest of them.

Solution:

In the figure, all intervals on which the derivative is positive are highlighted in color, which means the function itself increases on these intervals.

The length of the largest of them is 6.

Task 9.

The figure shows a graph of the derivative of a function defined on the interval. At what point on the segment does it take on the greatest value?

Solution:

Let's see how the graph behaves on the segment, which is what we are interested in only the sign of the derivative .

The sign of the derivative on is minus, since the graph on this segment is below the axis.

In the interim ( A,b), A X- is a randomly selected point in a given interval. Let's give the argument X incrementΔx (positive or negative).

The function y =f(x) will receive an increment Δу equal to:

Δy = f(x + Δx)-f(x).

At infinitesimal Δх incrementΔy is also infinitely small.

For example:

Let's consider solving the derivative of a function using the example of a freely falling body.

Since t 2 = t l + Δt, then

.

Having calculated the limit, we find:

The notation t 1 is introduced to emphasize the constancy of t when calculating the limit of the function. Since t 1 is an arbitrary time value, index 1 can be discarded; then we get:

It can be seen that the speed v, like the way s, There is function time. Function type v depends entirely on the type of function s, so the function s as if “producing” a function v. Hence the name " derivative function».

Consider another one example.

Find the value of the derivative of the function:

y = x 2 at x = 7.

Solution. At x = 7 we have y=7 2 = 49. Let's give the argument X increment Δ X. The argument will become equal 7 + Δ X, and the function will receive the value (7 + Δ x) 2.