3.1. Canonical equations of the line.

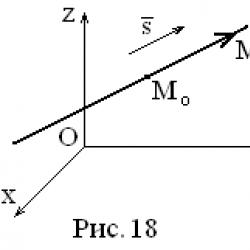
Let a straight line be given in the Oxyz coordinate system that passes through the point

(see Fig. 18). Let us denote by
a vector parallel to a given line. Vector called directing vector of a straight line. Let's take a point on a straight line
and consider the vector Vectors
are collinear, therefore their corresponding coordinates are proportional:

(3.3.1 )

These equations are called canonical equations straight.

Example: Write the equations of the line passing through the point M(1, 2, –1) parallel to the vector

Solution: Vector is the direction vector of the desired line. Applying formulas (3.1.1), we obtain:

These are the canonical equations of the line.

Comment: Turning to zero of one of the denominators means turning to zero of the corresponding numerator, that is, y – 2 = 0; y = 2. This line lies in the y = 2 plane, parallel to the Oxz plane.

3.2. Parametric equations of a straight line.

Let the straight line be given by the canonical equations

Let's denote
Then
The value t is called a parameter and can take any value:
.

Let's express x, y and z in terms of t:

(3.2.1 )

The resulting equations are called parametric equations of a straight line.

Example 1: Compose parametric equations of a straight line passing through the point M (1, 2, –1) parallel to the vector

Solution: The canonical equations of this line are obtained in the example of paragraph 3.1:

To find the parametric equations of a straight line, we apply the derivation of formulas (3.2.1):

So,
- parametric equations of a given line.

Answer:

Example 2. Write parametric equations for a line passing through the point M (–1, 0, 1) parallel to the vector
where A (2, 1, –1), B (–1, 3, 2).

Solution: Vector
is the direction vector of the desired line.

Let's find the vector
.

= (–3; 2; 3). Using formulas (3.2.1), we write down the equations of the straight line:

are the required parametric equations of the straight line.

3.3. Equations of a line passing through two given points.

A single straight line passes through two given points in space (see Fig. 20). Let points be given. Vector
can be taken as the direction vector of this line. Then the equations can be found directly them according to formulas (3.1.1):
).

(3.3.1)

Example 1. Compose canonical and parametric equations of a line passing through points

Solution: We apply formula (3.3.1)

We obtained the canonical equations of the straight line. To obtain parametric equations, we apply the derivation of formulas (3.2.1). We get

are parametric equations of a straight line.

Example 2. Compose canonical and parametric equations of a line passing through points

Solution: Using formulas (3.3.1) we obtain:

These are canonical equations.

Let's move on to parametric equations:

- parametric equations.

The resulting straight line is parallel to the oz axis (see Fig. 21).

Let two planes be given in space

If these planes do not coincide and are not parallel, then they intersect in a straight line:

This system of two linear equations defines a straight line as the line of intersection of two planes. From equations (3.4.1) one can go to canonical equations (3.1.1) or parametric equations (3.2.1). To do this you need to find a point
lying on a straight line, and the direction vector Point coordinates
we obtain from system (3.4.1), giving one of the coordinates an arbitrary value (for example, z = 0). Behind the guide vector you can take the vector product of vectors, that is

Example 1. Compose the canonical equations of the line

Solution: Let z = 0. Let us solve the system

Adding these equations, we get: 3x + 6 = 0
x = –2. Substitute the found value x = –2 into the first equation of the system and get: –2 + y + 1 = 0
y = 1.

So, period
lies on the desired line.

To find the direction vector of a straight line, we write down the normal vectors of the planes: and find their vector product:

We find the equations of the straight line using formulas (3.1.1):

Answer:
.

Another way: The canonical and parametric equations of the line (3.4.1) can be easily obtained by finding two different points on the line from the system (3.4.1), and then applying formulas (3.3.1) and the derivation of formulas (3.2.1).

Example 2. Compose canonical and parametric equations of the line

Solution: Let y = 0. Then the system will take the form:

Adding the equations, we get: 2x + 4 = 0; x = –2. Substitute x = –2 into the second equation of the system and get: –2 –z +1 = 0
z = –1. So, we found the point

To find the second point, let's set x = 0. We will have:

That is

We obtained the canonical equations of the straight line.

Let's compose the parametric equations of the straight line:

Answer:
;
.

3.5. The relative position of two lines in space.

Let straight
are given by the equations:

:
;
:

.

The angle between these lines is understood as the angle between their direction vectors (see Fig. 22). This angle we find using a formula from vector algebra:
or

(3.5.1)

If straight
perpendicular (
),That
Hence,

This is the condition of perpendicularity of two lines in space.

If straight
parallel (
), then their direction vectors are collinear (
), that is

(3.5.3 )

This is the condition of parallelism of two lines in space.

Example 1. Find the angle between straight lines:

A).
And

b).
And

Solution: A). Let's write down the direction vector of the straight line
Let's find the direction vector
planes included in the system. Then we find their vector product:

(see example 1 of clause 3.4).

Using formula (3.5.1) we obtain:

Hence,

b). Let's write down the direction vectors of these straight lines: Vectors
are collinear because their corresponding coordinates are proportional:

So it's straight
parallel (
), that is

Answer: A).
b).

Example 2. Prove perpendicularity of lines:

And

Solution: Let's write down the direction vector of the first straight line

Let's find the direction vector second straight line. To do this, we find normal vectors
planes included in the system: Let us calculate their vector product:

(See example 1 of paragraph 3.4).

Let us apply the condition of perpendicularity of lines (3.5.2):

The condition is met; therefore, the lines are perpendicular (
).

How to write equations of a straight line in space?

Equations of a straight line in space

Similar to a "flat" line, there are several ways in which we can define a line in space. Let's start with the canons - the point and the directing vector of the line:

If a certain point in space belonging to a line and the direction vector of this line are known, then the canonical equations of this line are expressed by the formulas:

The above notation assumes that the coordinates of the direction vector not equal to zero. We'll look at what to do if one or two coordinates are zero a little later.

Same as in the article Plane equation, for simplicity we will assume that in all problems of the lesson, actions are carried out in an orthonormal basis of space.

Example 1

Compose canonical equations of a line given a point and a direction vector

Solution: We compose the canonical equations of the line using the formula:

Answer:

And it’s a no brainer... although, no, it’s a no brainer at all.

What should you note about this very simple example? Firstly, the resulting equations DO NOT need to be reduced by one: . To be more precise, it is possible to shorten it, but it unusually hurts the eye and creates inconvenience when solving problems.

And secondly, in analytical geometry two things are inevitable - verification and testing:

Just in case, we look at the denominators of the equations and check - is it right the coordinates of the direction vector are written there. No, don’t think about it, we are not having a lesson at the Brake kindergarten. This advice is very important because it allows you to completely eliminate inadvertent mistakes. No one is insured, what if they copied it incorrectly? Will be awarded the Darwin Prize in Geometry.

The correct equalities are obtained, which means that the coordinates of the point satisfy our equations, and the point itself really belongs to this line.

The test is very easy (and quick!) to perform orally.

In a number of problems it is required to find some other point belonging to a given line. How to do it?

We take the resulting equations and mentally “pinch off”, for example, the left piece: . Now let's equate this piece to any number(remember that there was already a zero), for example, to one: . Since , then the other two “pieces” should also be equal to one. Essentially, you need to solve the system:

Let's check whether the found point satisfies the equations :

The correct equalities are obtained, which means that the point really lies on the given line.

Let's make the drawing in a rectangular coordinate system. At the same time, let’s remember how to correctly plot points in space:

Let's build a point:
– from the origin of coordinates in the negative direction of the axis we plot a segment of the first coordinate (green dotted line);
– the second coordinate is zero, so we “do not jerk” from the axis either to the left or to the right;
– in accordance with the third coordinate, measure three units upward (purple dotted line).

Construct a point: measure two units “towards you” (yellow dotted line), one unit to the right (blue dotted line) and two units down (brown dotted line). The brown dotted line and the point itself are superimposed on the coordinate axis, note that they are in the lower half-space and IN FRONT of the axis.

The straight line itself passes above the axis and, if my eye does not fail me, above the axis. It does not fail, I was convinced analytically. If the straight line passed BEHIND the axis, then you would have to erase with an eraser a piece of the line above and below the crossing point.

A straight line has an infinite number of direction vectors, for example:
(red arrow)

The result was exactly the original vector, but this was purely an accident, that’s how I chose the point. All direction vectors of a straight line are collinear, and their corresponding coordinates are proportional (for more details, see Linear (non) dependence of vectors. Basis of vectors). So, vectors will also be direction vectors of this line.

Additional information on creating three-dimensional drawings on checkered paper can be found at the beginning of the manual Graphs and properties of functions. In a notebook, multi-colored dotted paths to the points (see drawing) are usually thinly drawn with a simple pencil using the same dotted line.

Let's deal with special cases when one or two coordinates of the direction vector are zero. At the same time, we continue the training of spatial vision, which began at the beginning of the lesson. Plane equation. And again I will tell you the tale of the naked king - I will draw an empty coordinate system and convince you that there are spatial lines there =)

It’s easier to list all six cases:

1) For a point and a direction vector, the canonical equations of the line break down into three individual equations: .

Or in short:

Example 2: let's create equations of a straight line using a point and a direction vector:

What kind of line is this? The direction vector of the straight line is collinear to the unit vector, which means that this straight line will be parallel to the axis. The canonical equations should be understood as follows:
a) – “y” and “z” permanent, are equal specific numbers;
b) the variable “x” can take any value: (in practice, this equation is usually not written down).

In particular, the equations define the axis itself. Indeed, “x” takes on any value, and “y” and “z” are always equal to zero.

The equations under consideration can be interpreted in another way: let’s look, for example, at the analytical notation of the abscissa axis: . After all, these are equations of two planes! The equation specifies the coordinate plane, and the equation specifies the coordinate plane. You think correctly - these coordinate planes intersect along the axis. We will consider the method when a straight line in space is defined by the intersection of two planes at the very end of the lesson.

Two similar cases:

2) The canonical equations of a line passing through a point parallel to the vector are expressed by the formulas.

Such straight lines will be parallel to the coordinate axis. In particular, the equations specify the coordinate axis itself.

3) The canonical equations of a line passing through a point parallel to the vector are expressed by the formulas.

These straight lines are parallel to the coordinate axis, and the equations define the applicate axis itself.

Let's put the second three in the stall:

4) For a point and a direction vector, the canonical equations of the line break down into proportion and plane equation .

Example 3: let's compose the equations of a straight line using a point and a direction vector.

Let l- some straight line of space. As in planimetry, any vector

A =/= 0, collinear line l, called guide vector this straight line.

The position of the line in space is completely determined by specifying the direction vector and the point belonging to the line.

Let it be straight l with guide vector A passes through the point M 0, and M is an arbitrary point in space. Obviously, point M (Fig. 197) belongs to the line l if and only if the vector \(\overrightarrow(M_0 M)\) is collinear with the vector A , i.e.

\(\overrightarrow(M_0 M)\) = t a , t\(\in\) R. (1)

If points M and M 0 are specified by their radius vectors r And r 0 (Fig. 198) relative to some point O in space, then \(\overrightarrow(M_0 M)\) = r - r 0 , and equation (1) takes the form

r = r 0 + t a , t\(\in\) R. (2)

Equations (1) and (2) are called vector-parametric equations of a straight line. Variable t in vector-parametric equations the straight line is called parameter.

Let the point M 0 be a straight line l and the direction vector a are given by their coordinates:

M 0 ( X 0 ; at 0 , z 0), A = (A 1 ; A 2 ; A 3).

Then if ( X; y; z) - coordinates of an arbitrary point M of a straight line l, That

\(\overrightarrow(M_0 M) \) = ( x - x 0 ; y - y 0 ; z - z 0)

and vector equation (1) is equivalent to the following three equations:

x - x 0 = tа 1 , y - y 0 = tа 2 , z - z 0 = tа 3

$$ \begin(cases) x = x_0 + ta_1 \\ y = y_0 + ta_2 \\ z = z_0 + ta_3, \;\;t\in R\end(cases) (3)$$

Equations (3) are called parametric equations of the line in space.

Task 1. Write parametric equations for a line passing through a point

M 0 (-3; 2; 4) and having a direction vector A = (2; -5; 3).

In this case X 0 = -3, at 0 = 2, z 0 = 4; A 1 = 2; A 2 = -5; A 3 = 3. Substituting these values ​​into formulas (3), we obtain the parametric equations of this line

$$ \begin(cases) x = -3 - 2t \\ y = 2 - 5t \\ z = 4 + 3t, ​​\;\;t\in R\end(cases) $$

Let's exclude the parameter t from equations (3). This can be done because A =/= 0, and therefore one of the vector coordinates A is obviously different from zero.

Let first all coordinates be different from zero. Then

$$ t=\frac(x-x_0)(a_1),\;\;t=\frac(y-y_0)(a_2),\;\;t=\frac(z-z_0)(a_3) $$

and therefore

$$ \frac(x-x_0)(a_1)=\frac(y-y_0)(a_2)=\frac(z-z_0)(a_3) \;\; (4)$$

These equations are called canonical equations of the line .

Note that equations (4) form a system of two equations with three variables x, y And z.

If in equations (3) one of the vector coordinates A , For example A 1 is equal to zero, then by eliminating the parameter t, we again obtain a system of two equations with three variables x, y And z:

\(x=x_0, \;\; \frac(y-y_0)(a_2)=\frac(z-z_0)(a_3)\)

These equations are also called canonical line equations. For uniformity, they are also conventionally written in the form (4)

\(\frac(x-x_0)(0)=\frac(y-y_0)(a_2)=\frac(z-z_0)(a_3)\)

assuming that if the denominator is zero, then the corresponding numerator is also zero. These equations are the equations of a line passing through the point M 0 ( X 0 ; at 0 , z 0) parallel to the coordinate plane yOz, since its direction vector (0; A 2 ; A 3).

Finally, if in equations (3) there are two vector coordinates A , For example A 1 and A 2 are equal to zero, then these equations take the form

X = X 0 , y = at 0 , z = z 0 + t a 3 , t\(\in\) R.

These are the equations of a line passing through the point M 0 ( X 0 ; at 0 ; z 0) parallel to the axis Oz. For such a straight line X = X 0 , y = at 0 , a z- any number. And in this case, for uniformity, the equation of the straight line can be written (with the same reservation) in the form (4)

\(\frac(x-x_0)(0)=\frac(y-y_0)(0)=\frac(z-z_0)(a_3)\)

Thus, for any line in space one can write canonical equations (4), and, conversely, any equation of the form (4) provided that at least one of the coefficients A 1 , A 2 , A 3 is not equal to zero, defines some straight line in space.

Task 2. Write the canonical equations of a line passing through the point M 0 (- 1; 1, 7) parallel to the vector A = (1; 2; 3).

Equations (4) in this case are written as follows:

\(\frac(x+1)(1)=\frac(y-1)(2)=\frac(z-7)(3)\)

Let us derive the equations of a straight line passing through two given points M 1 ( X 1 ; at 1 ; z 1) and

M2( X 2 ; at 2 ; z 2). Obviously, we can take the vector a = (X 2 - X 1 ; at 2 - at 1 ; z 2 - z 1), and beyond the point M 0 through which a straight line passes, for example, point M 1. Then equations (4) will be written as follows:

\(\frac(x-x_1)(x_2 - x_1)=\frac(y-y_1)(y_2 - y_1)=\frac(z-z_1)(z_2 - z_1)\) (5)

These are the equations of a line passing through two points M 1 ( X 1 ; at 1 ; z 1) and

M2( X 2 ; at 2 ;z 2).

Task 3. Write the equations of a straight line passing through the points M 1 (-4; 1; -3) and M 2 (-5; 0; 3).

In this case X 1 = -4, at 1 = 1, z 1 = -3, X 2 = -5, at 2 = 0, z 2 = 3. Substituting these values ​​into formulas (5), we obtain

\(\frac(x+4)(-1)=\frac(y-1)(-1)=\frac(z+3)(6)\)

Task 4. Write the equations of the line passing through the points M 1 (3; -2; 1) and

M 2 (5; -2; 1/2).

After substituting the coordinates of points M 1 and M 2 into equations (5), we obtain

\(\frac(x-3)(2)=\frac(y+2)(0)=\frac(z-1)(-\frac(1)(2))\)

Canonical equations of the line

Formulation of the problem. Find the canonical equations of a line given as the line of intersection of two planes (general equations)

Solution plan. Canonical equations of a straight line with a direction vector passing through a given point , have the form

. (1)

Therefore, in order to write the canonical equations of a line, it is necessary to find its direction vector and some point on the line.

1. Since the straight line belongs to both planes simultaneously, its direction vector is orthogonal to the normal vectors of both planes, i.e. according to the definition of a vector product, we have

. (2)

2. Select some point on the line. Since the direction vector of the straight line is not parallel to at least one of the coordinate planes, the straight line intersects this coordinate plane. Consequently, the point of its intersection with this coordinate plane can be taken as a point on a line.

3. Substitute the found coordinates of the guide vector and point into the canonical equations of the straight line (1).

Comment. If the vector product (2) is equal to zero, then the planes do not intersect (parallel) and it is not possible to write the canonical equations of the line.

Problem 12. Write the canonical equations of the line.

Canonical equations of the line:

,

Where – coordinates of any point on a line, is its direction vector.

Let's find some point on the line. Let it be then

Hence, – coordinates of a point belonging to a line.

Let's look at the example solution.

Example.

Find the coordinates of any point on a line defined in space by the equations of two intersecting planes .

Solution.

Let us rewrite the system of equations in the following form

As a basis minor of the main matrix of the system, we take a non-zero minor of the second order , that is, z is a free unknown variable. Let's move the terms containing z to the right sides of the equations: .

Let us accept , where is an arbitrary real number, then .

Let's solve the resulting system of equations:

Thus, the general solution to the system of equations has the form , where .

If we take a specific value of the parameter , then we get a particular solution to the system of equations, which gives us the desired coordinates of a point lying on a given line. Let's take it then , therefore, is the desired point of the line.

You can check the found coordinates of a point by substituting them into the original equations of two intersecting planes:

Answer:

The direction vector of the line along which two planes intersect.

In a rectangular coordinate system, the directing vector of the straight line is inseparable from a straight line. When straight line a in a rectangular coordinate system in three-dimensional space is given by the equations of two intersecting planes and , then the coordinates of the directing vector of the straight line are not visible. Now we will show how to determine them.

We know that a line is perpendicular to a plane when it is perpendicular to any line lying in that plane. Then the normal vector of a plane is perpendicular to any non-zero vector lying in this plane. We will use these facts to find the direction vector of the line.

The straight line a lies both in the plane and in the plane. Therefore, the direction vector of line a is perpendicular to the normal vector plane, and normal vector plane Thus, the direction vector of straight line a is And :

The set of all direction vectors of a straight line and we can define it as , where is a parameter that can take any real values ​​other than zero.

Example.

Find the coordinates of any direction vector of a straight line, which is specified in the Oxyz rectangular coordinate system in three-dimensional space by the equations of two intersecting planes .

Solution.

The normal vectors of planes are the vectors And respectively. The directing vector of a straight line, which is the intersection of two given planes, is the vector product of normal vectors:

Answer:

Transition to parametric and canonical equations of a straight line in space.

There are cases in which using the equations of two intersecting planes to describe a straight line is not entirely convenient. Some problems are easier to solve if the canonical equations of a straight line in space are known: or parametric equations of a line in space of the form , where x 1 , y 1 , z 1 are the coordinates of a certain point on the line, a x , a y , a z are the coordinates of the directing vector of the line, and is a parameter that takes arbitrary real values. Let us describe the process of transition from linear equations of the form to canonical and parametric equations of a straight line in space.

In the previous paragraphs, we learned to find the coordinates of a certain point on a line, as well as the coordinates of a certain direction vector of a line, which is given by the equations of two intersecting planes. This data is sufficient to write down both the canonical and parametric equations of this line in a rectangular coordinate system in space.

Let's consider the solution to the example, and after that we will show another way to find the canonical and parametric equations of a line in space.

Example.

Solution.

Let us first calculate the coordinates of the directing vector of the straight line. To do this, we find the vector product of normal vectors And planes And :

That is, .

Now let's determine the coordinates of a certain point on a given line. To do this, we will find one of the solutions to the system of equations .

Determinant is different from zero, let us take it as the basis minor of the main matrix of the system. Then the variable z is free, we transfer the terms with it to the right sides of the equations, and give the variable z an arbitrary value:

We solve the resulting system of equations using the Cramer method:

Hence,

We accept , and we obtain the coordinates of the point on the line: .

Now we can write down the required canonical and parametric equations of the original line in space:

Answer:

And

Here is the second way to solve this problem.

When finding the coordinates of a certain point on a line, we solve the system of equations . In general, its solutions can be written in the form .

And these are exactly the required parametric equations of a straight line in space. If each of the resulting equations is resolved with respect to a parameter and then the right-hand sides of the equalities are equated, then we obtain the canonical equations of a straight line in space

Let us show the solution to the previous problem using this method.

Example.

A straight line in three-dimensional space is defined by the equations of two intersecting planes . Write canonical and parametric equations for this line.

Solution.

We solve this system of two equations with three unknowns (the solution is given in the previous example, we will not repeat it). In this case we get . These are the desired parametric equations of a straight line in space.

It remains to obtain the canonical equations of a straight line in space:

The resulting straight line equations are externally different from the equations obtained in the previous example, but they are equivalent, since they define the same set of points in three-dimensional space (and therefore the same straight line).

Answer:

And

Bibliography.

• Bugrov Ya.S., Nikolsky S.M. Higher mathematics. Volume one: elements of linear algebra and analytical geometry.
• Ilyin V.A., Poznyak E.G. Analytic geometry.