Распределения вероятностей случайных величин ; характеризуется функцией распределения

где - параметр формы кривой распределения, - параметр масштаба, - параметр сдвига. Семейство распределений (*) названо по имени В. Вейбулла , впервые использовавшего его для аппроксимации экспериментальных данных о прочности стали на разрыв при усталостпых испытаниях и предложившего методы оценки параметров распределения (*). В. р. принадлежит к асимптотич. распределению третьего типа крайних членов вариационного ряда. Оно широко используется для описания закономерностей отказов шарикоподшипников, вакуумных приборов, элементов электроники. Частными случаями В. р. являются экспоненциальное (р=1) и рэлеевское (р=2) распределения. Кривые функции распределения (*) не принадлежат семейству распределений Пирсона. Имеются вспомогательные таблицы для вычислений функции распределения Вейбулла (см. ). При квантиль уровня qравна

где - гамма-функция; вариации, асимметрия и эксцесс не зависят от , что облегчает их табулирование и создание вспомогательных таблиц для получения оценок параметров. При В. р. унимодально, равна , а функция опасности отказов не убывает. При функция монотонно убывает. Можно построить так. наз. вероятностную бумагу Вейбулла (см. ). На ней трансформируется в прямую, при образ имеет вогнутость, а при - выпуклость. Оценки параметров В. р. по методу квантилей приводят к уравнениям существенно более простым, чем по методу максимального правдоподобия. Совместная асимптотич. эффективность оценок параметров и (при ) по методу квантилей максимальна (и равна 0,64) при. использовании квантилей уровня 0,24 и 0,93. Функция распределения (*) хорошо аппроксимируется функцией распределения логнормального распределения

( - функция распределения нормированного нормального распределения,):

Лит :Weibull W., A statistical theory of the strength of materials, Stockh., 1939; Гнеденко Б. В., Беляев Ю. К., Соловьев А. Д., Математические методы в теории надежности, М., 1965; Jоhnsоn L., The statistical treatment of fatigue experiments, Amst., 1964; Крамер Г Математические методы статистики, пер. с англ., 2 изд., М, 1975. Ю. К. Беляев, Е. В. Чепурин.

Математическая энциклопедия. - М.: Советская энциклопедия . И. М. Виноградов . 1977-1985 .

Смотреть что такое "ВЕЙБУЛЛА РАСПРЕДЕЛЕНИЕ" в других словарях:

распределение - 3.38 распределение (allocation): Процедура, применяемая при проектировании системы (объекта) и направленная на распределение требований к значениям характеристик объекта по компонентам и подсистемам в соответствии с установленным критерием.… …

распределение Вейбулла - 1.48. распределение Вейбулла; распределение экстремальных значений типа III Распределение вероятностей непрерывной случайной величины Х с функцией распределения: где х ³ а; y = (x a)/b; а параметры ¥ < a < +¥, k > 0, b > 0. Примечание … Словарь-справочник терминов нормативно-технической документации

Плотность вероятности Функция распределения Обозначение {{{notation}}} Параметры коэффициент масштаба … Википедия

Распределение Вейбулла

Двухпараметрическое распределение Вейбулла является более гибким, чем экспоненциальное, которое может рассматриваться как частный случай первого. Плотность распределения Вейбулла

При 1/t0 = и m = 1 уравнение (8) превращается в плотность экспоненциального распределения. Величина 1/t0 определяет масштаб, а m - асимметрию (форму) распределения.

После интегрирования (8) от 0 до t получаем функцию распределения F(t), равную Q(t) :

Следовательно,

Отношение плотности (8) и вероятности (10) даёт интенсивность отказов

Основные графики распределения Вейбулла показаны на рис.4.

Двухпараметрическое распределение Вейбулла обладает исключительной гибкостью при аппроксимации эмпирических распределений и поэтому широко применяется в практических приложениях теории надёжности. Оно используется при описании законов надежности, как на участке приработки, так и при анализе процессов старения и износа.

Средняя наработка на отказ при распределении Вейбулла определяется из условия и равна

Рис.3.4. Графики распределения Вейбулла

где - гамма - функция;

Нормальное распределение

Двухпараметрическое нормальное (гауссово) распределение исключительно широко применяется в практических задачах теории надёжности. Параметрами этого распределения является - математическое ожидание случайной величины и - среднеквадратическое отклонение. Плотность нормального распределения определяется зависимостью

Функция распределения F(x) (рис.3.5) при нормальном законе определяется интегралом от плотности f(x) с пределами интегрирования от - до + .

Случайная величина t как и во всех задачах надёжности имеет смысл наработки объекта и поэтому определена на положительной полуоси чисел, а нормальный закон, как уже отмечалось, определён на всей числовой оси от - до + . В связи с этим в теории надёжности рассматривают усечённый нормальный закон, плотность которого определяется путём умножения (3.13) на постоянный множитель

где, a, b - левая и правая границы усечённого распределения.

F(a),F(b) - значения функций распределения нормального закона на левой и правой границах усечения.

Смысл постоянного множителя с становится ясным при рассмотрении графика плотности нормального распределения, представленного на рис.6.

Рис.5.

Известно, что площадь под кривой плотности распределения всегда должна быть равна единице, то есть в данном случае. Как показано на рис.6 для обеспечения этого условия кривую плотности усечённого нормального закона приходится сдвигать вверх и вправо путём умножения исходной плотности нормального закона на постоянный множитель. Соответственно будут меняться основные параметры: математическое ожидание и среднеквадратическое отклонение. Расчёты показывают, что при отношении / < 0.5 (коэффициент вариации) постоянный множитель c для усечённо- нормального закона близок к единице. Поэтому во многих практических задачах теории надёжности пользуются параметрами нормального закона распределения случайной наработки объекта до отказа. При этом математическое ожидание отождествляют со средней наработкой до отказа Т0.

Рис.6.

Вероятность безотказной работы при нормальном распределении равна

Вероятность отказа рассчитывается по формуле (при с 1)

Интенсивность отказов определяется отношением плотности к вероятности безотказной работы

Интегралы в выражениях (14)…(16) не выражаются через элементарные функции. Обычно они представляются через интеграл вероятности от параметра

для которого составлены таблицы.

С учётом (17) вероятность безотказной работы при нормальном законе определяется по формуле

Вопросы лекции:

Введение

Модели надёжности технических систем

Законы распределения времени безотказной работы

Введение

Количественные методы исследования технических объектов, особенно на этапах их проектирования и создания, всегда требуют построения математических моделей процессов и явлений. Под математической моделью обычно понимают взаимосвязанную совокупность аналитических и логических выражений, а также начальные и граничные условия, отражающие с определённым приближением реальные процессы функционирования объекта. Математическая модель – это информационный аналог натурного объекта, с помощью которого можно получить знания о создаваемом проекте. Считают, что способность вырабатывать предсказания является определяющим свойством модели. Всё это в полной мере относится к математическим моделям надёжности.

Под математической моделью надёжности понимается такая аналитически представляемая система, которая даёт полную информацию о надёжности объекта. При построении модели процесс изменения надёжности определённым образом упрощается, схематизируется. Из большого количества действующих на натурный объект факторов выделяются основные, изменение которых может вызвать заметные изменения надёжности. Связи между составными частями системы могут быть представлены аналитическими зависимостями также с определёнными приближениями. В результате выводы, получаемые на основе исследования модели надёжности объекта, содержат некоторую неопределённость.

Чем удачнее подобрана модель, чем лучше она отражает характерные особенности функционирования объекта, тем точнее будет оценена его надёжность и получены обоснованные рекомендации для принятия решения.

1. Модели надёжности технических систем

В настоящее время сложились общие принципы построения математических моделей надёжности. Модель строится только для определённого объекта, или точнее для группы однотипных объектов с учётом особенностей их будущей эксплуатации. Она должна удовлетворять следующим требованиям:

Модель должна учитывать максимальное количество факторов, оказывающих влияние на надёжность объекта;

Модель должна быть достаточно простой, чтобы с использованием типовых вычислительных средств получать выходные показатели надёжности в зависимости от изменения входных факторов.

Противоречивость этих требований не позволяет полностью формализовать построение моделей, что делает процесс создания моделей в определённой степени творческим.

Существует много классификаций моделей надёжности, одна их которых представлена на рис.1 1 .

Рис.1. Классификация моделей надёжности

Как следует из рис.1, все модели можно разделить на две большие группы: модели надёжности объектов и модели элементов. Модели надёжности элементов имеют больше физического содержания и более конкретизированы для элементов определённой конструкции. В этих моделях используются характеристики прочности материалов, учитываются нагрузки, действующие на конструкцию, рассматривается влияние условий эксплуатации на работу элементов. При исследовании этих моделей получают формализованное описание процессов возникновения отказов в зависимости от выделенных факторов.

Модели надёжности объектов создаются для формализованного описания с позиций надёжности процесса их функционирования как процесса взаимодействия элементов, составляющих данный объект. В такой модели взаимодействие элементов осуществляется только через наиболее существенные связи, влияющие на общую надёжность объекта.

Различают модели надёжности объектов параметрические и модели в терминах отказов элементов. Параметрические модели содержат функции случайных параметров элементов, что позволяет получить на выходе модели искомый показатель надёжности объекта. В свою очередь, параметры элементов могут являться функциями времени наработки объекта.

Модели, создаваемые в терминах отказов элементов, наиболее формализованы и являются основными при анализе надёжности сложных технических систем. Необходимым условием при создании таких моделей является чёткое описание признаков отказов каждого элемента системы. Модель отражает влияние отказа отдельного элемента на надёжность системы.

По принципам реализации моделей они различаются на аналитические, статистические и комбинированные (иначе функционально – статистические).

Аналитические модели содержат аналитические зависимости между параметрами, характеризующими надёжность системы, и выходным показателем надёжности. Для получения таких зависимостей приходится ограничивать количество значимых факторов и значительно упрощать физическую картину процесса изменения надёжности. В результате аналитические модели могут с достаточной точностью описывать только сравнительно простые задачи изменения показателей надёжности систем. С усложнением системы и увеличением количества факторов, влияющих на надёжность, на первый план выходят статистические модели.

Метод статистического моделирования позволяет решать многомерные задачи большой сложности за короткое время и с приемлемой точностью. С развитием вычислительной техники возможности этого метода расширяются.

Ещё большими возможностями обладает комбинированный метод, который предусматривает создание функционально – статистических моделей. В таких моделях для элементов создаются аналитические модели, а система в целом моделируется в статистическом режиме.

Выбор той или иной математической модели зависит от целей исследования надёжности объекта, от наличия исходной информации о надёжности элементов, от знания всех факторов, влияющих на изменение надёжности, от подготовленности аналитического аппарата для описания процессов накопления повреждений и возникновения отказов и многих других причин. В конечном итоге выбор модели осуществляет исследователь.

3. ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ МОДЕЛИ, НАИБОЛЕЕ ЧАСТО ИСПОЛЬЗУЕМЫЕ В РАСЧЕТАХ НАДЕЖНОСТИ

3.1. Распределение Вейбулла

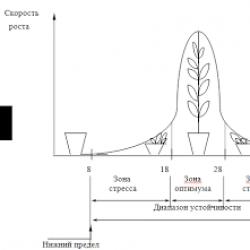
Опыт эксплуатации очень многих электронных приборов и значительного количества электромеханической аппаратуры показывает, что для них характерны три вида зависимостей интенсивности отказов от времени (рис. 3.1), соответствующих трем периодам жизни этих устройств .

Нетрудно увидеть, что этот рисунок аналогичен рис. 2.3, так как график функции l (t) соответствует закону Вейбулла. Указанные три вида зависимостей интенсивности отказов от времени можно получить, используя для вероятностного описания случайной наработки до отказа двухпараметрическое распределение Вейбулла . Согласно этому распределению плотность вероятности момента отказа

, (3.1)

где d - параметр формы (определяется подбором в результате обработки экспериментальных данных, d > 0); l - параметр масштаба, .

Интенсивность отказов определяется по выражению

(3.2)

Вероятность безотказной работы

, (3.3)

а средняя наработки до отказа

. (3.4)

Отметим, что при параметре d = 1 распределение Вейбулла переходит в экспоненциальное, а при d = 2 - в распределение Рэлея.

При d< 1 интенсивность отказов монотонно убывает (период приработки), а при монотонно возрастает (период износа), см. рис. 3.1. Следовательно, путем подбора параметра d можно получить, на каждом из трех участков, такую теоретическую кривую l (t), которая достаточно близко совпадает с экспериментальной кривой, и тогда расчет требуемых показателей надежности можно производить на основе известной закономерности.

Распределение Вейбулла достаточно близко подходит для ряда механических объектов (к примеру, шарикоподшипников), оно может быть использовано при ускоренных испытаниях объектов в форсированном режиме .

3.2. Экспоненциальное распределение

Как было отмечено в подразд. 3.1 экспоненциальное распределение вероятности безотказной работы является частным случаем распределения Вейбулла, когда параметр формы d = 1. Это распределение однопараметрическое, то есть для записи расчетного выражения достаточно одного параметра l = const . Для этого закона верно и обратное утверждение: если интенсивность отказов постоянна, то вероятность безотказной работы как функция времени подчиняется экспоненциальному закону:

. (3.5)

Среднее время безотказной работы при экспоненциальном законе распределения интервала безотказной работы выражается формулой:

. (3.6)

Заменив в выражении (3.5) величину l величиной 1 / Т 1 , получим . (3.7)

Отметим, что вероятность безотказной работы на интервале, превышающем среднее время Т 1 , при экспоненциальном распределении будет менее 0,368:

Р(Т 1) == 0,368 (рис. 3.2).

Длительность периода нормальной эксплуатации до наступления старения может оказаться существенно меньше Т 1 , то есть интервал времени на котором допустимо пользование экспоненциальной моделью, часто бывает меньшим среднего времени безотказной работы, вычисленного для этой модели. Это легко обосновать, воспользовавшись дисперсией времени безотказной работы. Как известно , если для случайной величины t задана плотность вероятности f(t) и определено среднее значение (математическое ожидание) Т 1 , то дисперсия времени безотказной работы находится по выражению:

(3.8)

и для экспоненциального распределения соответственно равна:

. (3.9)

После некоторых преобразований получим:

. (3.10) Таким образом, наиболее вероятные значения наработки, группирующиеся в окрестности Т 1 , лежат в диапазоне, то есть в диапазоне от t = 0 до t = 2Т 1 . Как видим, объект может отработать и малый отрезок времени и время t = 2Т 1 , сохранив l = const. Но вероятность безотказной работы на интервале 2Т 1 крайне низка: .

Важно отметить, что если объект отработал предположим, время t без отказа, сохранив l = соnst, то дальнейшее распределение времени безотказной работы будет таким, как в момент первого включения l = соnst.

Таким образом, отключение работоспособного объекта в конце интервала и новое его включение на такой же интервал множество раз приведет к пилообразной кривой (см. рис. 3.3).

Другие распределения не имеют указанного свойства. Из рассмотренного следует на первый взгляд парадоксальный вывод: поскольку за все время t устройство не стареет (не меняет своих свойств), то нецелесообразно проводить профилактику или замену устройств для предупреждения внезапных отказов, подчиняющихся экспоненциальному закону. Конечно, никакой парадоксальности этот вывод не содержит, так как предположение об экспоненциальном распределении интервала безотказной работы означает, что устройство не стареет. С другой стороны, очевидно, что чем больше время, на которое включается устройство, тем больше всевозможных случайных причин, которые могут вызвать отказ устройства. Это весьма важно для эксплуатации устройств, когда приходится выбирать интервалы, через которые следует производить профилактические работы с тем, чтобы сохранить высокую надежность работы устройства. Этот вопрос подробно рассматривается в работе .

Модель экспоненциального распределения часто используется для априорного анализа, так как позволяет не очень сложными расчетами получить простые соотношения для различных вариантов создаваемой системы. На стадии апостериорного анализа (опытных данных) должна проводиться проверка соответствия экспоненциальной модели результатам испытаний. В частности, если при обработке результатов испытаний окажется, что , то это является доказательством экспоненциальности анализируемой зависимости.

На практике часто бывает, что l№ const,однако, и в этом случае его можно применять для ограниченных отрезков времени. Это допущение оправдывается тем, что при ограниченном периоде времени переменную интенсивность отказов без большой ошибки можно заменить средним значением:

l (t) " l cр(t) = const.

3.3. Распределение Рэлея

Плотность вероятности в законе Рэлея (см. рис. 3.4) имеет следующий вид

¦ , (3.11)

где d* - параметр распределения Рэлея (равен моде этого распределения ). Его не нужно смешивать со среднеквадратическим отклонением: .

Интенсивность отказов равна:

Характерным признаком распределения Рэлея является прямая линия графика l (t), начинающаяся с начала координат.

Вероятность безотказной работы объекта в этом случае определится по выражению

. (3.12)

Средняя наработка до отказа

. (3.13)

3.4. Нормальное распределение (распределение Гаусса)

Нормальный закон распределения характеризуется плотностью вероятности вида

, (3.14)

где m x , s x - соответственно математическое ожидание и среднеквадратическое отклонение случайной величины х.

При анализе надежности электроустановок в виде случайной величины, кроме времени, часто выступают значения тока, электрического напряжения и других аргументов. Нормальный закон - это двухпараметрический закон, для записи которого нужно знать m x и s x .

Вероятность безотказной работы определяется по формуле

, (3.15)

а интенсивность отказов - по формуле

На рис. 3.5 изображены кривые l (t), Р(t) и ¦ (t) для случая s t << m t , характерного для элементов, используемых в системах автоматического управления .

В данном пособии показаны только наиболее распространенные законы распределения случайной величины. Известен целый ряд законов, так же используемых в расчетах надежности : гамма-распределение, -распределение, распределение Максвелла, Эрланга и др.

Следует отметить, что если неравенство s t << m t не соблюдается, то следует использовать усеченное нормальное распределение .

Для обоснованного выбора типа практического распределения наработки до отказа необходимо большое количество отказов с объяснением физических процессов, происходящих в объектах перед отказом.

В высоконадежных элементах электроустановок, во время эксплуатации или испытаний на надежность, отказывает лишь незначительная часть первоначально имеющихся объектов. Поэтому значение числовых характеристик, найденное в результате обработки опытных данных, сильно зависит от типа предполагаемого распределения наработки до отказа. Как показано в , при различных законах наработки до отказа, значения средней наработки до отказа, вычисленные по одним и тем же исходным данным, могут отличаться в сотни раз. Поэтому вопросу выбора теоретической модели распределения наработки до отказа необходимо уделять особое внимание с соответствующим доказательством приближения теоретического и экспериментального распределений (см. разд. 8).

3.5. Примеры использования законов распределения в расчетах надежности

Определим показатели надежности для наиболее часто используемых законов распределения времени возникновения отказов.

3.5.1. Определение показателей надежности при экспоненциальном законе распределения

Пример . Пусть объект имеет экспоненциальное распределение времени возникновения отказов с интенсивностью отказов l = 2,5 Ч 10 -5 1/ч.

Требуется вычислить основные показатели надежности невосстанавливаемого объекта за t = 2000 ч.

Решение.

q (2000) = 1 - Р (2000) = 1 - 0,9512 = 0,0488.

1. Используя выражение (2.5), вероятность безотказной работы в интервале времени от 500 ч до 2500 ч при условии, что объект проработал безотказно 500 ч равна

.

1. Средняя наработка до отказа

ч.

3.5.2. Определение показателей надежности при распределении Рэлея

Пример. Параметр распределения d* = 100 ч.

Требуется определить для t = 50 ч величины P(t), Q(t), l (t),Т 1 .

Решение.

Воспользовавшись формулами (3.11), (3.12), (3.13), получим

3.5.3. Определение показателей схемы при распределении Гаусса

Пример. Электрическая схема собрана из трех последовательно включенных типовых резисторов: ;

(в % задано значение отклонения сопротивлений от номинального).

Требуется определить суммарное сопротивление схемы с учетом отклонений параметров резисторов.

Решение.

Известно, что при массовом производстве однотипных элементов плотность распределения их параметров подчиняется нормальному закону . Используя правило 3 s (трех сигм), определим по исходным данным диапазоны, в которых лежат значения сопротивлений резисторов: ;

Следовательно,

Когда значения параметров элементов имеют нормальное распределение, и элементы при создании схемы выбираются случайным образом, результирующее значение R е является функциональной переменной, распределенной так же по нормальному закону , причем дисперсия результирующего значения, в нашем случае , определяется по выражению

Поскольку результирующее значение R е распределено по нормальному закону, то, воспользовавшись правилом 3 s , запишем

где - номинальные паспортные параметры резисторов.

Таким образом

Или

Данный пример показывает, что при увеличении количества последовательно соединенных элементов результирующая погрешность уменьшается. В частности, если суммарная погрешность всех отдельных элементов равна ± 600 Ом, то суммарная результирующая погрешность равна ± 374 Ом. В более сложных схемах, например в колебательных контурах, состоящих из индуктивностей и емкостей, отклонение индуктивности или емкости от заданных параметров сопряжено с изменением резонансной частоты, и возможный диапазон ее изменения можно предусмотреть методом, аналогичным с расчетом резисторов .

3.5.4. Пример определения показателей надежности неремонтируемого объекта по опытным данным

Пример. На испытании находилось N о = 1000 образцов однотипной невосстанавливаемой аппаратуры, отказы фиксировались через каждые 100 часов.

Требуется определить в интервале времени от 0 до 1500 часов. Число отказов на соответствующем интервале представлено в табл. 3.1. Таблица 3.1
Исходные данные и результаты расчетов

Номер i-го интервала	,ч	шт.		,1/ч
1	0 -100	50	0,950
2	100 -200	40	0,910	0,430
3	200 -300	32	0,878	0,358
4	300 - 400	25	0,853	0,284
5	400 - 500	20	0,833	0,238
6	500 - 600	17	0,816	0,206
7	600 -700	16	0,800	0,198
8	700 - 800	16	0,784	0,202
9	800 - 900	15	0,769	0,193
10	900 -1000	14	0,755	0,184
11	1000 -1100	15	0,740	0,200
12	1100 -1200	14	0,726	0,191
13	1200 -1300	14	0,712	0,195
14	1300 -1400	13	0,699	0,184
15	1400 -1500	14	0,685	0,202 Ч

Решение. .

Средняя наработка до отказа, при условии отказов всех N o объектов, определяется по выражению

, где tj - время отказа j-го объекта (j принимает значения от 0 до N о). В данном эксперименте из N о = 1000 объектам отказало всего объектов. Поэтому по полученным опытным данным можно найти только приближенное значение средней наработки до отказа. В соответствии с поставленной задачей воспользуемся формулой из : при r Ј N о, (3.16)

где tj - наработка до отказа j-го объекта (j принимает значения
от 1 до r); r - количество зафиксированных отказов (в нашем случае r = 315); tr - наработка до r-го (последнего) отказа. Из графика видно, что после периода приработки t і 600 ч интенсивность отказов приобретает постоянную величину. Если предположить, что и в дальнейшем l будет постоянной, то период нормальной эксплуатации связан с экспоненциальной моделью наработки до отказа испытанного типа объектов. Тогда средняя наработка до отказа

ч.

Таким образом, из двух оценок средней наработки до отказа
= 3831 ч и T 1 = 5208 ч надо выбрать ту, которая более соответствует фактическому распределению отказов. В данном случае можно предполагать, что если бы провести испытания до отказа всех объектов, то есть r = N о, достроить график рис. 3.6 и выявить время, когда l начнет увеличиваться, то для интервала нормальной эксплуатации (l = const) следует брать среднюю наработку до отказа T 1 = 5208 ч.

В заключение по данному примеру отметим, что определение средней наработки до отказа по формуле (2.7), когда r << N о, дает грубую ошибку. В нашем примере

ч.

Если вместо N о поставим количество отказавших объектов
r = 315, то получим

ч.

В последнем случае не отказавшие за время испытания объекты в количестве N о - r = 1000-315 = 685 шт. вообще в оценку не попали, то есть была определена средняя наработка до отказа только 315 объектов. Эти ошибки достаточно распространены в практических расчетах.

Это распределение чаще всего используется при исследовании интенсивности отказов для периодов приработки и старения. На примере распределения сроков службы изоляции некоторых элементов электрической сети подробно рассмотрены физические процессы, приводящие к старению и отказу изоляции и описываемые распределением Вейбулла.

Надежность наиболее распространенных элементов электрических сетей, таких как силовые трансформаторы и кабельные линии, в значительной степени определяется надежностью работы изоляции, «прочность» которой изменяется в течение эксплуатации. Основной характеристикой изоляции электромеханических изделий является ее электрическая прочность, которая в зависимости от условий эксплуатации и вида изделия определяется механической прочностью, эластичностью, исключающей образование остаточных деформаций, трещин, расслоений под воздействием механических нагрузок, т.е. неоднородностей.

Однородность и монолитность структуры изоляции и ее высокая теплопроводность исключают возникновение повышенных местных нагревов, неизбежно приводящих к увеличению степени неоднородности электрической прочности. Разрушение изоляции при функционировании элемента происходит в основном в результате нагревания токами нагрузок и температурных воздействий внешней среды.

Рассмотрев два основных фактора (тепловое старение и механическая нагрузка), влияющих па срок службы изоляции, которые к тому же тесно связаны между собой, можно сделать вывод, что как усталостные явления в изоляции, так и тепловое ее старение в значительной степени зависят от качества изготовления и материала электротехнического изделия, от однородности материала изоляции, обеспечивающей отсутствие местных нагревов (так как трудно предположить, что откажет вся изоляция, т.е. пробой произойдет по всей площади изоляции).

Микротрещипы, расслоения и другие неоднородности материала случайно распределены в отношении своего положения и своей величины по всему объему (площади) изоляции. При воздействии переменных неблагоприятных условий как теплового, так и электродинамического характера неоднородности материала увеличиваются: например, микротрещина распространяется в глубь изоляции и при случайном повышении напряжения может вызвать пробой изоляции. Причиной отказа может быть даже небольшая неоднородность материала.

Естественно предположить, что число неблагоприятных воздействий (тепловых или электромеханических), вызывающих пробой изоляции, есть функция, убывающая в зависимости от размеров неоднородности. Это число минимально для наибольшей по размерам неоднородности (трещины, расслоения и др.).

Следовательно, число неблагоприятных воздействий, определяющее срок службы изоляции, должно подчиняться закону распределения минимальной случайной величины из совокупности независимых случайных величин, соответствующих различным по размерам неоднородностям:

где Г и - время безотказной работы всей изоляции; Г и, - время безотказной работы /"-го участка (/" = 1,2, п).

Таким образом, для определения закона распределения времени безотказной работы такого объекта, как изоляция элемента электрической сети, необходимо найти закон распределения минимального времени безотказной работы совокупности всех участков. Наибольший интерес представляет случай, когда законы распределения времени безотказной работы отдельных участков имеют различный характер, но вид законов распределения одинаков, т.е. резко выраженных отличий у участков нет.

С позиций надежности участки такой системы соответствуют последовательному соединению. Функция распределения времени безотказной работы такой системы из п участков, соединенных последовательно:

Рассмотрим общий случай, когда распределение Р(г) имеет так называемый «порог чувствительности», т.е. элемент гарантированно не откажет в интервале времени (0, /о) (в частном случае /о может быть равно 0). Очевидно, что функция Р(1ц + Д/) > 0 - всегда неубывающая функция аргумента.

Для системы можно получить асимптотический закон распределения времени безотказной работы:

Если распределение не имеет порога чувствительности / 0 , то закон распределения будет иметь вид

где с - некоторый постоянный коэффициент, с > 0; а - показатель Вейбулла.

Этот закон называется распределением Вейбулла. Он довольно часто используется при аппроксимации распределения времени безотказной работы системы с конечным числом последовательно (с точки зрения надежности) соединенных элементов (протяженные кабельные линии со значительным числом муфт и др.).

Плотность распределения времени безотказной работы

При а = 1 плотность распределения превращается в обычную показательную функцию (рис. 3.3).

Для интенсивности отказов при плотности распределения по закону Вейбулла получим

Интенсивность отказов для этого закона в зависимости от параметра распределения а может расти, оставаться постоянной (показательный закон) и уменьшаться (рис. 3.4).

При а = 2 функция распределения времени безотказной работы совпадает с законом Рэлея, а при а » 1 достаточно хорошо аппроксимируется нормальным законом распределения в окрестности среднего времени безотказной работы.

Рис. 3.3.

Рис. 3.4.

Как видно из рис. 3.3 и 3.4, экспоненциальный закон распределения является частным случаем закона Вейбулла при а = 1 (А. = const).

Закон Вейбулла очень удобен для вычислений, но требует эмпирического подбора параметров А. и а для имеющейся зависимости А.(/).

Математическое ожидание (среднее время) безотказной работы и дисперсия при распределении по закону Вейбулла:

где Г(х) - гамма-функция, определяемая по таблице Г(.г) (см. прил. 2); с - некоторый постоянный коэффициент, определяющий вероятность появления к элементарных повреждений на интервале времени (0, /)